Física - Conceptos y Problemas
David Giuliodori
Movimiento Rectilíneo
En este movimiento, el cuerpo considerado como partícula, sólo podrá moverse en una dimensión (trayectoria rectilínea). Vamos a disntiguir dos tipos de MR:
Movimiento Rectilíneo Uniforme (MRU)
Movimiento Rectilíneo Uniformemente Variado (MRUV)
Empezaremos definiendo dos conceptos que son fundamentales en este tipo de movimiento:
Definición 1.1 (Velocidad). La velocidad de un cuerpo es la relación que existe entre el espacio que recorre y el tiempo que emplea en recorrerlo. Esta podrá ser constante o variable, dependiendo del tipo de movimiento que se trate.
\[\begin{aligned} \label{vel} v=\frac{\Delta x}{\Delta t}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}} \end{aligned}\] donde \(x_{1}\) y \(x_{2}\) son los espacios inicial y final respectivamente, y \(t_{1}\) y \(t_{2}\) los tiempos iniciales y finales.
Definición 1.2 (Aceleración). La velocidad de un cuerpo es la relación que existe entre el cambio de velocidad que experimenta y el tiempo que tarda en experimentarlo. Un cuerpo que modifica su velocidad a medida que transcurre el tiempo, está asumiendo que tiene una cierta aceleración.
\[\begin{aligned} \label{acel} a=\frac{\Delta v}{\Delta t}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}} \end{aligned}\] donde \(v_{1}\) y \(v_{2}\) son las velocidades inicial y final respectivamente.
Movimiento Rectilíneo Uniforme
Los cuerpos que se mueven con movimiento rectilíneo uniforme, se caracterizan por recorrer espacios iguales en tiempos iguales. En otras palabras, la velocidad es constante y como consecuencia, la aceleración es nula. Por lo tanto:
\[\begin{aligned} \label{mru_v} v=\frac{\Delta x}{\Delta t}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=k \end{aligned}\]
\[\begin{aligned} \label{mru_a} a=\frac{\Delta v}{\Delta t}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=0 \end{aligned}\]
Si despejamos \(x_{2}\) de la ecuación [mru_v] se obtiene:
\[\begin{aligned} \label{mru_x} x_{2}=x_{1}+v \cdot \Delta t \end{aligned}\] esta ecuación es la que llamaremos ecuación del espacio.
Recordemos cómo era la ecuación de una función lineal:
\[\begin{aligned} y=a+b \cdot x \end{aligned}\]
Por lo tanto, se puede observar que \(x_{2}\) es una función lineal respecto de \(\Delta t\), donde el espacio inicial \(x_{1}\) es la ordenada al origen, y la velocidad la pendiente de la recta. Gráficamente tenemos:
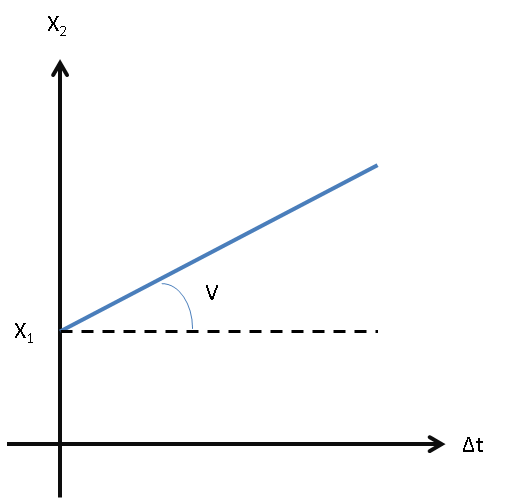 |
Si la velocidad es positiva la recta es creciente, si la velocidad es negativa la recta decrece. Cabe destacar que los gráficos del espacio en función del tiempo sólo tienen sentido en el primer cuadrante, debido a que no existen ni tiempos ni espacios negativos.
Dado que en MRU la velocidad es constante a lo largo del tiempo, cuando graficamos tenemos:
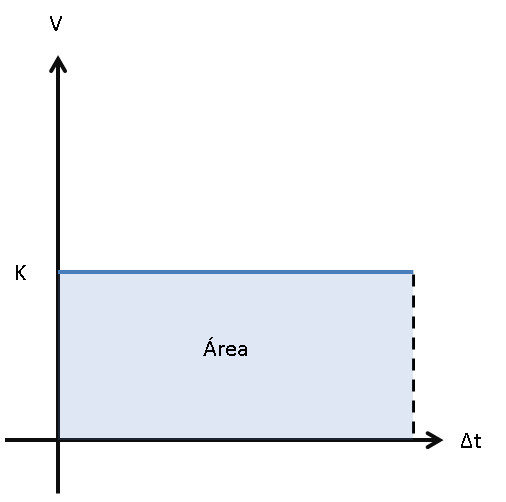 |
En este gráfico, el área representa el espacio recorrido, es decir:
\[\begin{aligned} \label{mru_a1} \textbf{Área}&=&\textbf{Base} \cdot \textbf{Altura} \nonumber \\ &=& \Delta t \cdot v = \Delta x \end{aligned}\]
Ejemplo 1.1. Un auto se desplaza a 80 km/h
durante 3 horas. Calcular la distancia recorrida por el auto.
Solución
Usando la ecuacion [mru_x] tenemos,
\[\begin{aligned} x_{2}=v \cdot \Delta t= 80 km/h \cdot 3 h= 240 km \end{aligned}\]
\(\blacksquare\)
Ejemplo 1.2. Escribir la ecuación del espacio
del siguiente gráfico 1.1.
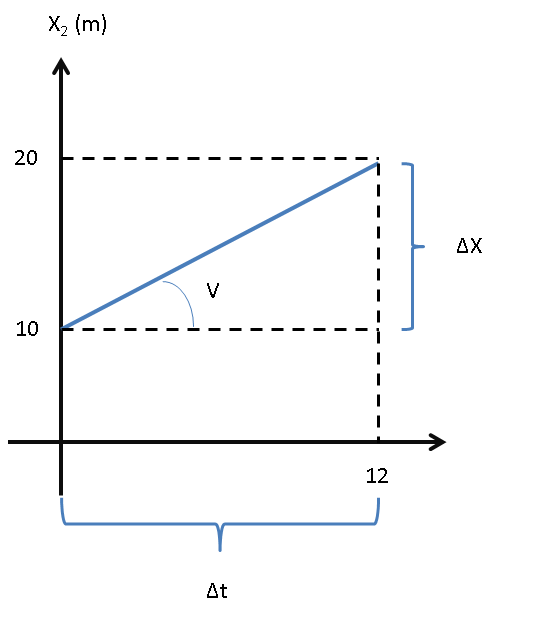 |
Solución
Usando la ecuacion [mru_x] tenemos,
\[\begin{aligned} x_{2}=10 m + \frac{10 m}{12 s}\cdot \Delta t= 10 m + 0,83 m/s \cdot \Delta t \end{aligned}\]
\(\blacksquare\)
Ejercicios
Pasar de unidades las siguientes velocidades:
de 36 km/h a m/s.
de 10 m/s a km/h.
de 30 km/min a cm/s.
) de 50 m/min a km/h.
Un móvil recorre 98 km en 2 h, calcular:
Su velocidad.
¿Cuántos kilómetros recorrerá en 3 h con la misma velocidad?.
Respuestas: 49 km/h y 147 km
Se produce un disparo a 2,04 km de donde se encuentra un policía, ¿cuánto tarda el policía en oírlo si la velocidad del sonido en el aire es de 330 m/s?
Respuestas: 6,18 s
La velocidad de sonido es de 330 m/s y la de la luz es de 300.000 km/s. Se produce un relámpago a 50 km de un observador.
¿Qué recibe primero el observador, la luz o el sonido?
¿Con qué diferencia de tiempo los registra?
Respuestas: La luz. La diferencia de tiempo es 151,51 s
¿Cuánto tarda en llegar la luz del sol a la Tierra?, si la velocidad de la luz es de 300.000 km/s y el sol se encuentra a 150.000.000 km de distancia.
Respuestas: 500 s
Un auto de fórmula 1, recorre la recta de un circuito, con velocidad constante. En el tiempo t1 = 0,5 s y t2 = 1,5 s, sus posiciones en la recta son x1 = 3,5 m y x2 = 43,5m. Calcular:
¿A qué velocidad se desplaza el auto?
¿En qué punto de la recta se encontraría a los 3 s?
Respuestas: 40 m/s y 123,5 m
¿Cuál será la distancia recorrida por un móvil a razón de 90 km/h, después de un día y medio de viaje?
Respuestas: 3240 km
¿Cuál de los siguientes móviles se mueve con mayor velocidad: el (a) que se desplaza a 120 km/h o el (b) que lo hace a 45 m/s?
Respuestas: El movil b
¿Cuál es el tiempo empleado por un móvil que se desplaza a 75 km/h para recorrer una distancia de 25.000 m?
Respuestas: 0,33 hs
¿Qué tiempo empleará un móvil que viaja a 80 km/h para recorrer una distancia de 640 km?
Respuestas: 8 hs
Movimiento Rectilíneo Uniformemente Variado
Es aquel en el que un móvil se desplaza sobre una trayectoria recta
estando sometido a una aceleración constante, como consecuancia
experimenta cambios de velocidades iguales en intervalos de tiempo
iguales. Un ejemplo de este tipo de movimiento es el de caída libre
vertical, en el cual la aceleración interviniente, y considerada
constante, es la que corresponde a la gravedad.
También puede definirse el movimiento como el que realiza una partícula
que partiendo del reposo es acelerada por una fuerza constante.
Por lo tanto podemos escribir:
\[\begin{aligned} \label{mruv_a} a=\frac{\Delta v}{\Delta t}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}} \neq 0 \end{aligned}\]
Despejando \(v_{2}\) de la ecuación [mruv_a] tenemos:
\[\begin{aligned} \label{mruv_v} v_{2}=v_{1}+a \cdot \Delta t \end{aligned}\]
Nuevamente aquí sucede algo similar a lo visto en MRU con la ecuación
del espacio, es decir que \(v_{1}\) es
la ordenada al origen, y la aceleración la pendiente (que puede ser
positiva o negativa).
A la ecuación [mruv_v] la llamaremos la ecuación
de la velocidad. El gráfico de esta ecuación es equivalente a
la ecuación del espacio del MRU ([mru_x]), por lo
que el gráfico de esta ecuación es el siguiente:
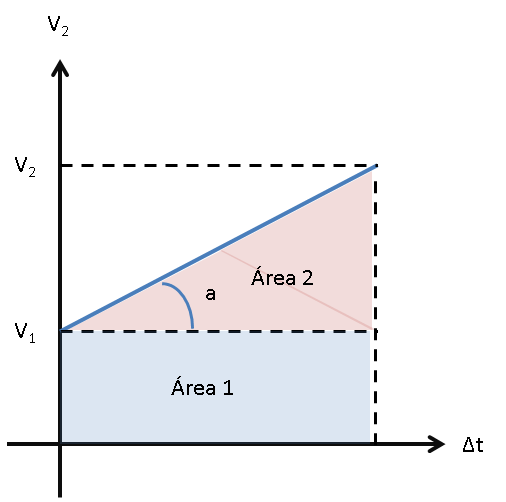 |
Nuevamente, el área del gráfico representa el espacio total recorrido. Calculando las áreas tenemos:
\[\begin{aligned} \textbf{Área 1}&=&\textbf{Base} \cdot \textbf{Altura} \nonumber \\ &=& \Delta t \cdot v_{1} \\ \textbf{Área 2}&=&\frac{\textbf{Base} \cdot \textbf{Altura}}{2} \nonumber \\ &=& \frac{\Delta t \cdot (v_{2}-v_{1})}{2} \\ \textbf{Área}&=&\textbf{Área 1} + \textbf{Área 2} \nonumber \\ &=&\Delta t \cdot v_{1} + \frac{\Delta t \cdot (v_{2}-v_{1})}{2} = \Delta x \end{aligned}\]
Ahora, reemplazando el resultado obtenido en la ecuación [mruv_v] por \(v_{2}\), tenemos:
\[\begin{aligned} \Delta x&=&\Delta t \cdot v_{1} + \frac{\Delta t \cdot (v_{2}-v_{1})}{2} \nonumber \\ &=& \Delta t \cdot v_{1} + \frac{\Delta t \cdot (v_{1}+a \cdot \Delta t-v_{1})}{2} \end{aligned}\]
Simplificando y reescribiendo la ecuación, se obtiene:
\[\begin{aligned} \Delta x= \Delta t \cdot v_{1} + \frac{a \cdot \Delta t^{2}}{2} \end{aligned}\]
Por último, descomponemos \(\Delta x=x_{2}-x_{1}\), por lo que:
\[\begin{aligned} \label{mruv_x1} x_{2}=x_{1}+ v_{1} \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^{2} \end{aligned}\]
La ecuación [mruv_x] es la que llamaremos
ecuación del espacio del MRUV.
Ahora, recordemos cómo era la ecuación de la función cuadrática:
\[\begin{aligned} y=a\cdot x^{2}+b \cdot x+c \end{aligned}\]
Por lo que se puede observar, de la ecuación [mruv_x], \(x_{2}\) es una función cuadrática respecto del tiempo, donde la ordenada al origen (coeficiente \(c\)) viene dado por \(x_{1}\); \(1/2\cdot a\), que se corresponde con el coeficiente \(a\) de la función cuadrática, determina si las parábolas van hacia arriba (aceleración positiva) o hacia abajo (aceleración negativa); y por último, la velocidad inicial \(v_{1}\) es el coeficiente \(b\) de la función.
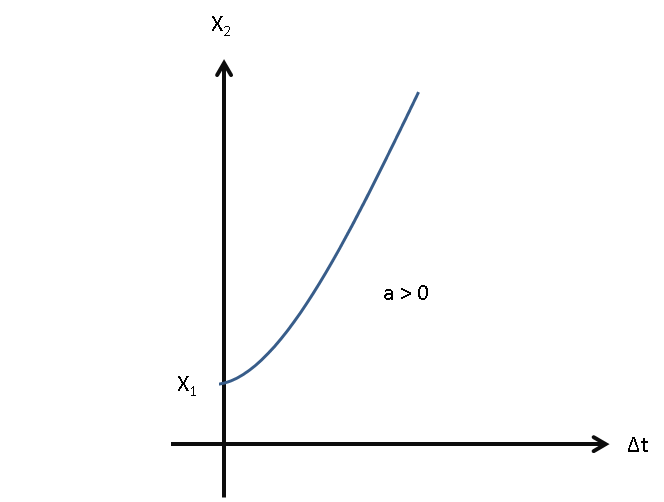 |
Cabe destacar que si la aceleración toma el valor cero, la ecuaciones [mruv_v] y [mruv_x] son las siguientes:
\[\begin{aligned}
\label{mruv_x}
x_{2}&=&x_{1}+ v_{1} \cdot \Delta t \nonumber \\
v_{2}&=&v_{1}
\end{aligned}\] que son efectivamente las ecuaciones
correspondiente al MRU, donde la velocidad es constante (velocidad
inicial y final iguales) y el espacio es lineal respecto del
tiempo.
Existe una relación muy importante y que es muy útil en muchos casos
prácticos que surge de combinar las ecuaciones [mruv_v] y [mruv_x], que relaciona las velocidades con
la aceleración y el espacio:
\[\begin{aligned} \label{mruv_rel} v_{2}^{2}-v_{1}^{2}&=&2 a \Delta x \end{aligned}\]
Ejemplo 1.3. Usted frena su Porsche desde la
velocidad de 85 km/h hasta los 45 km/h en una distancia de 105 m.
Calcular a) la aceleración suponiendo que sea constante durante el
intervalo b) ¿Qué tanto tiempo transcurrió durante el intervalo? c) Si
usted fuera a seguir frenando con la misma aceleración, ¿qué tiempo le
tomará detenerse y qué distancia adicional le tocará recorrer?
Solución
Usando la ecuacion [mruv_rel] y despejando la aceleración tenemos,
\[\begin{aligned} a=\frac{v_{2}^{2}-v_{1}^{2}}{2\cdot \Delta x}=\frac{\left(12,5 m/s\right)^{2}-\left(23,61 m/s\right)^{2}}{2\cdot 105 m}=-1,91 m/s^{2} \end{aligned}\]
Para calcular el tiempo usamos la ecuacion [mruv_v] y despejamos el tiempo,
\[\begin{aligned} \Delta t=\frac{v_{2}-v_{1}}{a}=\frac{12,5m/s-23,61 m/s}{-1,91 m/s^{2}}=5,8s \end{aligned}\]
Si fueramos a seguir frenando, tendríamos que calcular lo siguiente:
\[\begin{aligned} \Delta t=\frac{v_{2}-v_{1}}{a}=\frac{0-12,5 m/s}{-1,91 m/s^{2}}=6,5s \end{aligned}\]
Para calcular el espacio recorrido hasta frenar usamos la ecuación [mruv_x],
\[\begin{aligned} x_{2}&=&x_{1}+ v_{1} \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^{2} \nonumber \\ &=&12,5 m/s \cdot 6,5 s + \frac{1}{2} \left(-1,91 m/s^{2}\right) \cdot \left(6,5 s\right)^{2}=41 m \end{aligned}\]
\(\blacksquare\)
En resumen, podemos escribir las dos variantes del moviemiento rectilíneo en el siguiente cuadro:
| MRU | MRUV | |
|---|---|---|
| Aceleración | 0 | Constante |
| Velocidad | Constante | \(v_{2}=v_{1}+a \cdot \Delta t\) |
| Función lineal respecto al tiempo | ||
| Espacio | \(x_{2}=x_{1}+v \cdot \Delta t\) | \(x_{2}=x_{1}+ v_{1} \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^{2}\) |
| Función lineal respecto al tiempo | Función cuadrática respecto al tiempo |
Ejercicios
Un automóvil que viaja a una velocidad constante de 120 km/h, demora 10 s en detenerse. Calcular:
¿Qué espacio necesitó para detenerse?
¿Con qué velocidad chocaría a otro vehículo ubicado a 30 m del lugar donde aplicó los frenos?
Respuestas: \(x_{2}=166,6 m\) y \(v_{2}=30 m/s\)
Un ciclista que va a 30 km/h, aplica los frenos y logra detener la bicicleta en 4 segundos. Calcular:
¿Qué desaceleración produjeron los frenos?
¿Qué espacio necesito para frenar?
Un avión, cuando toca pista, acciona todos los sistemas de frenado, que le generan una desaceleración de 20 m/s\(^{2}\), necesita 100 metros para detenerse. Calcular:
¿Con qué velocidad toca pista?
¿Qué tiempo demoró en detener el avión?
Un camión viene disminuyendo su velocidad en forma uniforme, de 100 km/h a 50 km/h. Si para esto tuvo que frenar durante 1.500 m. Calcular:
¿Qué desaceleración produjeron los frenos?
¿Cuánto tiempo empleó para el frenado?
La bala de un rifle, cuyo cañón mide 1,4 m, sale con una velocidad de 1.400 m/s. Calcular:
¿Qué aceleración experimenta la bala?
¿Cuánto tarda en salir del rifle?
Una partícula se encuentra en reposo en el instante t=0 s. Si su gráfica \(a-t\) es la que se muestra en la figura, determinar las gráficas \(v-t\) y \(x-t\).
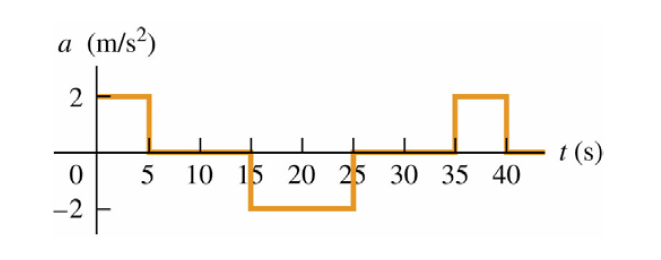
Un móvil que se desplaza con velocidad constante, aplica los frenos durante 25 s, y recorre una distancia de 400 m hasta detenerse. Determinar:
¿Qué velocidad tenía el móvil antes de aplicar los frenos?
¿Qué desaceleración produjeron los frenos?
Un auto marcha a una velocidad de 90 km/h. El conductor aplica los frenos en el instante en que ve el pozo y reduce la velocidad hasta 1/5 de la inicial en los 4 s que tarda en llegar al pozo. Determinar a qué distancia del obstáculo el conductor aplico los frenos, suponiendo que la aceleración fue constante.
Un automóvil parte del reposo con una aceleración constante de 3 m/s\(^{2}\), determinar:
¿Qué velocidad tendrá a los 8 s de haber iniciado el movimiento?
¿Qué distancia habrá recorrido en ese lapso?
A partir del gráfico \(v-t\) mostrado a continuación, calcular la velocidad inicial (\(v_{0}\)) del móvil, si se sabe que la distancia total recorrida es de 102 m (suponer \(T=16 s\)).
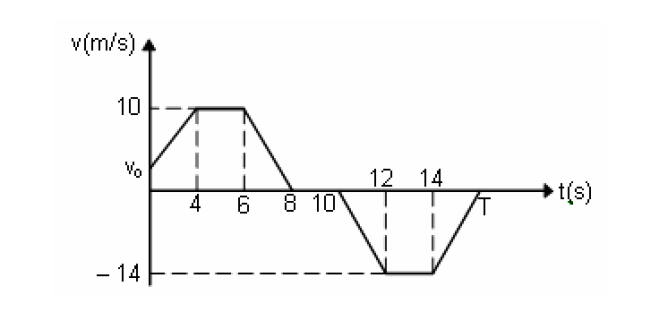
Un móvil que se desplaza con velocidad constante, acelera durante 30 segundos, y recorre una distancia de 350 m hasta alcanzar los 160 km/h. Determinar:
Velocidad inicial
Aceleración
Según el siguiente gráfico \(V-t\), calcular:
Identificar el tipo de movimiento en cada tramo
Espacio total recorrido
Velocidad media para todo el recorrido
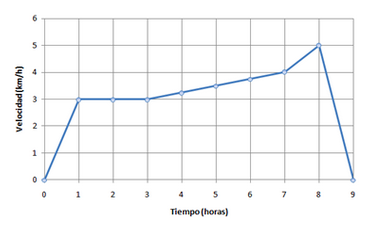
Según el siguiente gráfico \(V-t\), calcular:
Identificar el tipo de movimiento en cada tramo
Espacio total recorrido
Velocidad media para todo el recorrido
Aceleración en cada tramo
Tiro Oblicuo
Un ejemplo de tiro oblicuo es el movimiento de un proyectil, el
movimiento ideal de una pelota de béisbol o el de una pelota de golf. En
nuestro análisis supondremos que se desprecia el rozamiento del aire.
Además, por simplificación, consideraremos sólo el movimiento de caída
del objeto. Entonces, en el eje vertical (lo llamaremos \(y\)) sólo actuará la gravedad, es decir un
movimiento variado, mientras que en el eje horizontal (lo llamaremos
\(x\)) será un movimiento rectilíneo
uniforme.
Por lo que tenemos:
| Eje Vertical (\(y\)) | Eje Horizontal (\(x\)) | |
|---|---|---|
| Espacio | \(x_{2}=x_{1}+ v_{1} \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^{2}\) | \(x_{2}=x_{1}+v \cdot \Delta t\) |
| Velocidad | \(v_{2}=v_{1} + a \cdot \Delta t\) | \(v=\textbf{constante}\) |
Si consideramos la velocidad inicial en \(y\) igual a cero, y teniendo en cuenta que el espacio recorrido en el eje vertical corresponde a la altura desde donde es lanzado el objeto, entonces:
| Eje Vertical (\(y\)) | Eje Horizontal (\(x\)) | |
|---|---|---|
| Espacio | \(h= \frac{1}{2} g \cdot \Delta t^{2}\) | \(x_{2}=v \cdot \Delta t\) |
| Velocidad | \(v_{2}= g \cdot \Delta t\) | \(v=\textbf{constante}\) |
Despejando el tiempo de la ecuación de espacio del eje vertical, podemos calcular el tiempo de caída o de impacto del objeto:
\[\begin{aligned} \label{caida} \Delta t=\sqrt{\frac{2\cdot h}{g}} \end{aligned}\]
Además, la velocidad de impacto o velocidad de caída del eje \(y\) es:
\[\begin{aligned} v_{2}=\sqrt{2\cdot h \cdot g} \end{aligned}\]
Cabe destacar, que el tiempo de caída es el tiempo de alcance del objeto, es decir el tiempo que tarda en recorrer el espacio en el eje \(x\), que es el mismo tiempo que tarda en caer.
Ejemplo 1.4. En un concurso en dejar caer un
paquete sobre un blanco, el aeroplano de unos de los concursantes está
volando a una velocidad constante de 155 km/h y a una altura de 225 m
hacia el punto directamente arriba del plano. ¿Cuál es el tiempo de
caída y a qué distancia se encuentra el blanco?
Solución
Hallaremos el tiempo de caída usando la ecuación [caida],
\[\begin{aligned} \Delta t=\sqrt{\frac{2\cdot h}{g}}=\sqrt{\frac{2\cdot 225 m}{9,8 m/s^{2}}}=6,78s \end{aligned}\]
La distancia horizontal recorrida por el paquete en este tiempo viene dada por:
\[\begin{aligned} x_{2}=v \cdot \Delta t = 43,05 m/s \cdot 6,78 s=291,9m \end{aligned}\]
\(\blacksquare\)
Ejercicios
Un piloto, volando horizontalmente a 500 m de altura y 1080 km/h, lanza una bomba. Calcular:
¿Cuánto tarda en oír la explosión?
¿A qué distancia se encontraba el objetivo?
Un avión que vuela a 2000 m de altura con una velocidad de 800 km/h suelta una bomba cuando se encuentra a 5000 m del objetivo. Determinar:
¿A qué distancia del objetivo cae la bomba?
¿Cuánto tarda la bomba en llegar al suelo?
¿Dónde está el avión al explotar la bomba?
Un proyectil es disparado desde un acantilado de 20 m de altura en dirección paralela al río, éste hace impacto en el agua a 2000 m del lugar del disparo. Determinar:
¿Qué velocidad inicial tenía el proyectil?
¿Cuánto tardó en tocar el agua?
Una pelota está rodando con velocidad constante sobre una mesa de 2 m de altura, a los 0,5 s de haberse caído de la mesa esta a 0,2 m de ella. Calcular:
¿Qué velocidad traía?
¿A qué distancia de la mesa estará al llegar al suelo?
¿Cuál era su distancia al suelo a los 0,5 s?
Un avión vuela horizontalmente con velocidad vA = 900 km/h a una altura de 2000 m, suelta una bomba que debe dar en un barco cuya velocidad es vB = 40 km/h con igual dirección y sentido. Determinar:
¿Qué tiempo tarda la bomba en darle al barco?
¿Con qué velocidad llega la bomba al barco?
¿Qué distancia recorre el barco desde el lanzamiento hasta el impacto?
¿Cuál será la distancia horizontal entre el avión y el barco en el instante del lanzamiento?
¿Cuál será la distancia horizontal entre el avión y el barco en el instante del impacto?
Alcance y Encuentro
En este caso particular, en el momento de encuentro/alcance los cuerpos cumplen con la condición de que el espacio y el tiempo son los mismos. Entonces igualando las ecuaciones de espacio de los cuerpos generalmente se resuelve el problema.
Ejemplo 1.5. Pasa un auto a 72 km/h por un
puesto de control policial. En el mismo instante sale en su persecución
una moto de policia, que parte del reposo, con una aceleración de 3
\(m/s^{2}\). ¿Dónde y cuando lo
alcanzará?
Solución
Para hallar la solución, primero hay que identificar el tipo de movimiento en cada vehículo. La moto, dado que tiene aceleración de 3 \(m/s^{2}\), es un MRUV, y el auto, que se mueve a velocidad constante, es MRU.
Para el auto tenemos que la ecuación de espacio viene dada por:
\[\begin{aligned} \label{auto} x_{2}&=&x_{1}+v \cdot \Delta t \nonumber \\ x_{2}&=&72 km/h \cdot \Delta t \end{aligned}\]
Para la moto tenemos:
\[\begin{aligned} \label{moto} x_{2}&=&x_{1}+ v_{1} \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^{2} \nonumber \\ x_{2}&=& 0 \cdot \Delta t + \frac{1}{2} 3 m/s^{2} \cdot \Delta t^{2} \nonumber \\ e&=& \frac{1}{2} 3 m/s^{2} \cdot \Delta t^{2} \nonumber \\ \end{aligned}\]
Igualando ambas ecuaciones (transformando todo a las mismas unidades), dado que en el momento de ecuentro la moto y el auto han recorrido el mismo espacio, se tiene:
\[\begin{aligned} 20 m/s \cdot \Delta t=\frac{1}{2} 3 m/s^{2} \cdot \Delta t^{2} \end{aligned}\]
Despejando \(\Delta t\), se llega a:
\[\begin{aligned} \Delta t&=&\frac{20 m/s}{0.5 \cdot 3 m/s^{2}} \nonumber \\ \Delta t&=&13,33 s \end{aligned}\]
Una vez calculado el tiempo, se reemplaza en cualquiera de las ecuaciones [auto] o [moto] ese valor para así obtener el espacio recorrido. Por ejemplo usaremos la ecuación del espacio correspondiente al auto ([auto]), entonces:
\[\begin{aligned} x_{2}&=&20 m/s \cdot 13,33 s \nonumber \\ x_{2}&=&266,6 m \end{aligned}\]
La conslusión del problema es que la moto alcanza al auto luego de recorrer 266,6 m en 13,33 s.
\(\blacksquare\)
Ejercicios
En una esquina, una persona ve como un muchacho pasa en su auto a una velocidad de 20 m/s. Diez segundos después, una patrulla de la policía pasa por la misma esquina persiguiéndolo a 30 m/s. Considerando que ambos mantienen su velocidad constante, resolver gráfica y analíticamente:
¿A qué distancia de la esquina, la policía alcanzará al muchacho?
¿En qué instante se produce el encuentro?
En un instante pasa por A un cuerpo con movimiento rectilíneo uniforme de 20 m/s. Cinco segundos después, pasa en su persecución, por el mismo punto A, otro cuerpo animado de movimiento rectilíneo uniforme, de velocidad 30 m/s. ¿Cuándo y dónde lo alcanzará?, resolver gráfica y analíticamente.
Un móvil sale de una localidad A hacia B con una velocidad de 80 km/h, en el mismo instante sale de la localidad B hacia A otro a 60 km/h, A y B se encuentran a 600 km. Calcular:
¿A qué distancia de A se encontraran?
¿En qué instante se encontraran?
Un móvil sale de una localidad A hacia B con una velocidad de 80 km/h, 90 minutos después sale desde el mismo lugar y en su persecución otro móvil a 27,78 m/s. Calcular:
¿A qué distancia de A lo alcanzará?
¿En qué instante lo alcanzará?
Dos móviles pasan simultáneamente, con M.R.U., por dos posiciones A y B distantes entre si 3 km, con velocidades va = 54 km/h y vb = 36 km/h, paralelas al segmento AB y del mismo sentido. Hallar analíticamente y gráficamente:
La posición del encuentro.
El instante del encuentro.
Dos móviles pasan simultáneamente, con M.R.U., por dos posiciones A y B distantes entre si 6 km, con velocidades va = 36 km/h y vb = 72 km/h, paralelas al segmento AB y del sentido opuesto. Hallar analíticamente y gráficamente:
La posición del encuentro.
El instante del encuentro.
Dos puntos A y B están separados por una distancia de 180 m. En un mismo momento pasan dos móviles, uno desde A hacia B y el otro desde B hacia A, con velocidades de 10 m/s y 20 m/s respectivamente. Hallar analíticamente y gráficamente:
¿A qué distancia de A se encontraran?
El instante del encuentro.
En una obra en construcción se tira verticalmente hacia arriba desde los 15 m de altura un martillo con velocidad inicial de 40 m/s, en el mismo momento, a 8 m de altura, sube un montacarga con velocidad constante de 2 m/s, si el martillo no pudo ser atajado, ¿cuánto tiempo después y a qué altura chocará con el montacarga?
Se largan dos ciclistas, uno con velocidad constante de 40 km/h, el otro partiendo del reposo con una aceleración de 1000 km/h\(^{2}\), calcular:
¿Cuándo el primer ciclista será alcanzado por el segundo?
¿A qué distancia de la salida?
¿Qué velocidad tendrá el segundo ciclista en el momento del encuentro?
Un automovilista pasa por un puesto caminero a 120 km/h superando la velocidad permitida, a los 4 s un policía sale a perseguirlo acelerando constantemente, si lo alcanza a los 6000 m, calcular:
¿Cuánto dura la persecución?
¿Qué aceleración llevaba el policía?
¿Qué velocidad tenía el policía en el momento del encuentro?
Un motociclista detenido en una esquina arranca con una aceleración de \(0,003 m/s^{2}\). En el mismo momento un automóvil lo pasa y sigue con una velocidad constante de 70 km/h, calcular:
¿Cuánto tarda el motociclista en alcanzar al automóvil?
¿A qué distancia de la esquina ocurre esto?
El maquinista de un tren que avanza con una velocidad v1 advierte delante de él, a una distancia d, la cola de un tren de carga que se mueve en su mismo sentido, con una velocidad v2 constante, menor que la suya. Frena entonces, con aceleración constante, determinar el mínimo valor del módulo de dicha aceleración, para evitar el choque.
Un jugador de fútbol ejecuta un tiro libre, lanzando la pelota con un ángulo de 30 grados con respecto a la horizontal y con una velocidad de 20 m/s. Un segundo jugador corre para alcanzar la pelota con una velocidad constante, partiendo al mismo tiempo que ella desde 20 m más delante de la posición de disparo. Despreciando el tiempo que necesita para arrancar, calcular con qué velocidad debe correr para alcanzar la pelota cuando ésta llegue al suelo.
En el instante en que un semáforo da luz verde, un automóvil, que había estado detenido en el cruce, arranca recto con una aceleración constante de \(2 m/s^{2}\). Al mismo tiempo una camioneta, con velocidad constante de 10 m/s, le da alcance y lo pasa. Determinar:
¿A qué distancia de su punto de partida el automóvil alcanzará a la camioneta?
¿A qué velocidad lo hará?
Un auto va desde Córdoba hacia Carlos Paz (36 km de distancia), partiendo desde el reposo con una aceleración de 0,1 m/s\(^{2}\). Al mismo tiempo parte un auto desde Carlos Paz hacia Córdoba con una velocidad constante de 80 km/h.
¿A qué distancia de Córdoba se encontraran los autos?
¿Cuanto tiempo tardarán en encontrarse?
¿Cuál es la velocidad de cada auto al momento de encuentro? Realice un gráfico de las ecuaciones del espacio, marcando los puntos principales
Movimiento Circular Uniforme
En física, el movimiento circular uniforme describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.
Aceleraciones y Velocidades en MCU
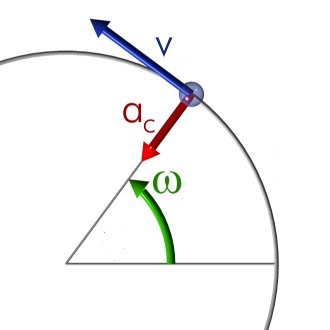
Definición 2.1. Aceleración centrípeta
La aceleración centrípeta es una magnitud relacionada con el cambio de dirección de la velocidad de una partícula en movimiento cuando recorre una trayectoria curvilínea. Cuando una partícula se mueve en una trayectoria curvilínea, aunque se mueva con rapidez constante (por ejemplo el MCU), su velocidad cambia de dirección, ya que es un vector tangente a la trayectoria, y en las curvas dicha tangente no es constante.
\[\begin{aligned} \label{ac} a_{c}=\frac{v^{2}}{R} \end{aligned}\]
Definición 2.2. Velocidad angular
La velocidad angular es la variación del desplazamiento angular por unidad de tiempo:
\[\begin{aligned} \omega=\frac{\Delta\theta}{\Delta t} \end{aligned}\]
 |
Definición 2.3. Frecuencia
La frecuencia mide el número de revoluciones o vueltas completadas por el móvil dividido el tiempo que tarda en realizarlas.
\[\begin{aligned} f=\frac{vueltas}{\Delta t} \end{aligned}\]
Definición 2.4. Período
Tiempo necesario para realizar una vuelta
\[\begin{aligned} f=\frac{1}{T} \end{aligned}\]
Por otra parte, dado que el perímetro de una circunferencia viene dado por \(P=2\pi R\), entonces la distancia total recorrida viene dada por:
\[\begin{aligned} \Delta x= 2\pi R \cdot \textbf{vueltas} \end{aligned}\]
Relación entre velocidad angular y velocidad lineal o tangencial
La velocidad angular y la velocidad lineal se relacionan a través del radio de la circunferencia, es decir:
\[\begin{aligned} v=\omega \cdot R \end{aligned}\]
Esta relación es sumamente útil a la hora de resolver ejercicios en los que, por ejemplo no se conoce el ángulo recorrido.
Ejemplo 2.1. Un moto circula a velocidad
constante por una curva de 150 m de radio. Si la velocidad de la moto es
de 72 km/h, calcular la aceleración centrípeta de la moto.
Solución
Usando la ecuación [ac] tenemos:
\[\begin{aligned} a_{c}=\frac{v^{2}}{R}=\frac{\left( 20 m/s \right)^{2}}{150 m}=2,67 m/s^{2} \end{aligned}\]
\(\blacksquare\)
Ejemplo 2.2. Sobre un carrete que gira a velocidad angular constante \(\omega=7 rad/s\), se enrollan 21 m de hilo, siempre con el mismo radio \(r=0,18\) m. Calcular:
El tiempo que tarda en enrollar los 21 m
El número de vueltas que ha dado el carrete
El ángulo girado en radianes
La velocidad lineal del hilo
La aceleración centrípeta que sufre un punto de la periferia del carrete
Solución
\[\begin{aligned} \Delta t=\frac{\Delta x}{v}=\frac{\Delta x}{\omega R}=\frac{21 m}{7 rad/s \cdot 0,18 m}=16,66s \end{aligned}\]
\[\begin{aligned} P=2\pi R=2\pi 0,18m=1,13 m \end{aligned}\]
Por regla de tres simple se calcula que la cantidad de vueltas es 18,56.
\[\begin{aligned} \theta=\omega t=7rad/s \cdot 16,66 s=116,66 rad \end{aligned}\]
\[\begin{aligned} V=\omega R=7rad/s 0,18m=1,26 m/s \end{aligned}\]
\[\begin{aligned} a_{c}=\frac{V^{2}}{R}=\frac{\left(1,26m/s\right)^{2}}{0,18m}=8,82m/s^{2} \end{aligned}\]
\(\blacksquare\)
Ejercicios
Un disco de 8 cm de diámetro, ha girado 81 vueltas en un tiempo total de 108 s. Suponiendo contante la velocidad angular, calcular:
La distancia recorrida por un punto de la periferia
El ángulo girado en radianes
La velocidad lineal o tangencial de un punto de la periferia
La velocidad angular del disco
La aceleración centrípeta
Respuestas: 2035,75 cm; 508,88 rad; 18,85 cm/s; 4,71 rad/s; 88,74 cm/s\(^{2}\)
Sobre un carrete que gira a velocidad angular constante \(\omega=5 rad/s\), se enrollan 18 m de hilo, siempre con el mismo radio \(r=0,15\) m. Calcular:
El tiempo que tarda en enrollar los 18 m
El número de vueltas que ha dado el carrete
El ángulo girado en radianes
La velocidad lineal del hilo
La aceleración centrípeta que sufre un punto de la periferia del carrete
Respuesta: 24 s; 19,10 vueltas; 120 rad; 0,75 m/s; 3,75 m/s\(^{2}\)
Un auto circula a velocidad constante por una curva de autopista de 1000 m de radio. Si la aceleración centrípeta no debe exceder 1,2 m/s\(^{2}\), calcular:
La máxima velocidad permitida
Respuesta: 34 m/s
Un coche circula por una curva de autopista de 300 m de radio a una velocidad de 90 km/h. Calcular:
Cuánto vale la componente normal (centrípeta) de su aceleración
Respuesta: 2,1 m/s\(^{2}\)
La Luna gira alrededor de la Tierra haciendo una revolución completa en 27,3 días. Suponiendo que la órbita es circular y que tiene un radio de \(3,82 \times 10^{8}\)m. ¿Cuál es la magnitud de la aceleración de la Luna hacia la Tierra?
Calcule la velocidad de un satélite artificial de la Tierra, suponiendo que está viajando a una altitud de 210 km, donde la \(g=9,2\) m/s\(^{2}\). El radio de la Tierra es de 6370 km.
Un tren realiza un viaje entre París y Le Mans, en Francia, donde puede adquirir una velocidad máxima de 310 km/h.
Si el tren toma una curva a esta velocidad, y la aceleración experimentada por los pasajeros no debe superar los 0,05 \(g\) (9,8 m/s\(^{2}\)) ¿cuál es el radio de la vía más pequeña que puede tolerarse?
Si existiese una curva con radio de 0,94 km ¿A qué valor debería disminuir el tren su velocidad?
Un niño hace girar una piedra en un círculo horizontal situado a 1,9 metros sobre el suelo por medio de una cuerda de 1,4 metros de longitud. La cuerda se rompe y la piedra sale disparada horizontalmente, golpeando el suelo a 11 metros de distancia. ¿Cuál fue la aceleración de la piedra mientras estaba en movimiento circular?
Un automóvil, cuyo velocímetro indica en todo instante 72 km/h, recorre el perímetro de una pista circular en un minuto. Calcular:
La velociadd angular
El radio de la circunsferencia
La aceleración centrípeta
Calcular la velocidad angular y la frecuencia con que debe girar una rueda, para que los puntos situados a 50cm de su eje estén sometidos a una aceleración que sea 500 veces la de la gravedad.
Un piloto de avión bien entrenado aguanta aceleraciones de hasta 8 veces la de la gravedad, durante tiempos breves, sin perder el conocimiento.
Para un avión que vuela a 2300 km/h, ¿cuál será el radio de giro mínimo que puede soportar?
¿Que sucede con el piloto, si el radio de giro es de 4800 m a la velocidad calculada en el punto anterior? Justifique su respuesta con el planteo y cálculo correspondiente.
Una bicicleta recorre 40 m en 5 s.
Hallar el período de sus ruedas si el radio es de 50 cm.
Determinar el tiempo que tardará en recorrer 300 m.
Respuestas: 0,4 s ; 37,5 s
Una varilla de 3 m de longitud gira respecto a uno de sus extremos a 20 r.p.m.: Calcular:
El período y el nº de vueltas que dará en 15 s.
La velocidad del otro extremo de la varilla.
La velocidad de un punto de la varilla situado a 1 m del extremo fijo.
La velocidad de un punto de la varilla situado a 2 m del extremo fijo.
Respuestas: 3 s; 5 rev; 2\(\pi\) m/s; 2,1 m/2; 4,2 m/s
Hallar el periodo de la aguja horaria de un reloj.
Respuestas: 43200 s
Una rueda de coche tarda 20 s en recorrer 500 m. Su radio es de 40 cm. Hallar el nº de vueltas que dará al recorrer los 500 m y las r.p.m. con que gira.
Respuestas: 199 rev; 596,8 rpm
La velocidad angular de una rueda es de 2 rad/s y su radio, 60 cm. Hallar la velocidad y la aceleración centrípeta de un punto del extremo de la rueda.
Respuestas: 1,2 m/s; 2,4 m/s\(^{2}\)
Un auto se desplaza a 124 km/h, cuando ve que hay un cartel de curva a 250 metros, por lo que frena hasta la velocidad adecuada para tomar una curva de 252,52 metros de radio, que admite una aceleración centrípeta máxima de 1,1 m/s\(^{2}\). Una vez finalizada la curva, el auto vuelve a acelerar hasta llegar a los 110 km/h en un tiempo de 10 segundos. Calcular:
Tiempo empleado para frenar antes de llegar a la curva
Aceleración durante el frenado
Velocidad lineal durante la curva
Velocidad angular
Espacio recorrido después de la curva
Aceleración alcanzada después de la curva
¿Qué hubiese sucedido si el auto frenaba hasta los 80 km/h antes de llegar a la curva?
Trabajo y Energía
Trabajo
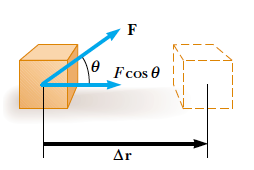
Definición 3.1. Trabajo
En mecánica clásica, el trabajo que realiza una fuerza se define como el producto de ésta por el camino que recorre su punto de aplicación y por el coseno del ángulo que forman el uno con el otro.1 El trabajo es una magnitud física escalar que se representa con la letra (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
\[\begin{aligned} W=F \cdot d \cdot \cos{\alpha} \end{aligned}\]
La unidad del \(W\) es el Joule (\(J=\frac{Kg \cdot m^2}{s^{2}}\))
 |
Definición 3.2. Potencia
Potencia (símbolo P) es la cantidad de trabajo efectuado por unidad de tiempo
\[\begin{aligned} P=\frac{W}{t} \end{aligned}\]
La unidad de la potencia es el Watts (\(W=\frac{J}{s}\))
Energía
Se define como la capacidad para realizar un trabajo. La energía por ser justamente la capacidad de realizar un trabajo, se mide con las mismas unidades que el trabajo (\(J\)).
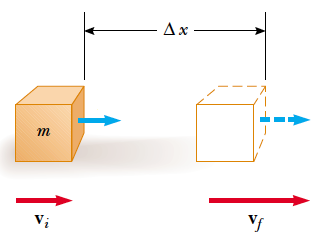
Definición 3.3. Energía Cinética
En un sistema físico, la energía cinética de un cuerpo es energía que surge en el fenómeno del movimiento. Está definida como el trabajo necesario para acelerar un cuerpo de una masa dada desde el reposo hasta la velocidad que posee. Una vez conseguida esta energía durante la aceleración, el cuerpo mantiene su energía cinética salvo que cambie su rapidez o su masa. Para que el cuerpo regrese a su estado de reposo se requiere un trabajo negativo de la misma magnitud que su energía cinética. Suele abreviarse con letra \(E_{c}\).
\[\begin{aligned} E_{c}=\frac{1}{2}m \cdot v^{2} \end{aligned}\]
 |
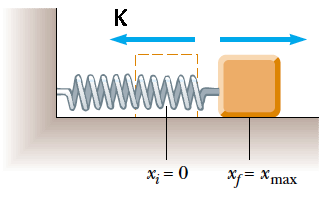
Definición 3.4. Energía Elástica
La energía elástica o energía de deformación es el aumento de energía interna acumulado en el interior de un sólido deformable como resultado del trabajo realizado por las fuerzas que provocan la deformación. Suponiendo que tenemos un resorte con constante elástica \(K\), y con una deformación \(\Delta X\), entonces la energía elástica se define como:
\[\begin{aligned} E_{E}=\frac{1}{2}K \cdot \Delta X^{2} \end{aligned}\]
La unidad con la que se mide \(K\) generalmente será N/m.
 |
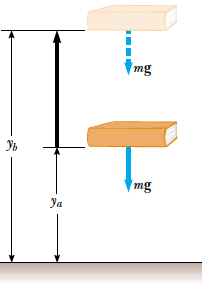
Definición 3.5. Energía Potencial
La energía potencial gravitatoria es la energía asociada con la fuerza gravitatoria. Esta dependerá de la altura relativa de un objeto a algún punto de referencia, la masa, y la fuerza de la gravedad.
\[\begin{aligned} E_{p}=m \cdot g \cdot h \end{aligned}\]
 |
Ley de conservación de la energía
La ley de la conservación de la energía constituye el primer principio de la termodinámica y afirma que la cantidad total de energía en cualquier sistema aislado (sin interacción con ningún otro sistema) permanece invariable con el tiempo, aunque dicha energía puede transformarse en otra forma de energía. En resumen, la ley de la conservación de la energía afirma que la energía no puede crearse ni destruirse, sólo se puede cambiar de una forma a otra, por ejemplo, cuando la energía potencial se transforma en energía cinética en la caída libre de un objeto. Dicho de otra forma :la energía puede transformarse de una forma a otra o transferirse de un cuerpo a otro, pero en su conjunto permanece estable (o constante).
\[\begin{aligned} E_{c1}+E_{p1}+E_{E1}=E_{c2}+E_{p2}+E_{E2} \end{aligned}\]
Ejemplo 3.1. El resorte de un rifle se comprime
3,2 cm desde su estado de relajación, y en el cañón se introduce una
bala de 12 g de masa. ¿A qué velocidad saldrá la bala del cañón al
disparar el arma? La constante del resorte es 7,5 N/cm. Suponga que no
existe fricción y que el cañón del rifle está horizontal.
Solución
Aplicando la ley de conservación de la energía tenemos,
\[\begin{aligned} E_{c1}+E_{p1}+E_{E1}&=&E_{c2}+E_{p2}+E_{E2} \nonumber \\ 0+0+\frac{1}{2}KX^{2}&=&\frac{1}{2}mv^{2}+0+0 \end{aligned}\]
Resolviendo para \(v\) nos da:
\[\begin{aligned} v=X \sqrt{\frac{K}{m}}=0,032m \sqrt{\frac{750 N/m}{12 \times 10^{-3} kg}}=8,0 m/s \end{aligned}\]
\(\blacksquare\)
Ejemplo 3.2. Una montaña rusa eleva lentamente
una carrito lleno de pasajeros a una altura de 25 m, desde donde se deja
caer hacia abajo. Despreciando la fricción en el sistema, ¿a qué
velocidad llegará el carrito al fondo?
Solución
Aplicando la ley de conservación de la energía tenemos,
\[\begin{aligned} E_{c1}+E_{p1}+E_{E1}&=&E_{c2}+E_{p2}+E_{E2} \nonumber \\ 0+m g h+0&=&\frac{1}{2}mv^{2}+0+0 \end{aligned}\]
Resolviendo para \(v\) nos da:
\[\begin{aligned} v=\sqrt{2 g h}=\sqrt{2 \cdot 9,8 m/s^{2} 25 m}=22 m/s \end{aligned}\]
\(\blacksquare\)
Ejemplo 3.3. Una persona le gusta realizar el deporte extremo de caída libre. Si la persona pesa 70 kg, y sabiendo que la altura a la que se larga del avión es a 4000 metros sobre el nivel del suelo, calcular
¿Qué velocidad tendrá la persona cuando esta a 1500 m de altura?
Si la velocidad máxima a la cuál se debe abrir el paracaídas es a los 250 km/h, ¿a qué altura deberá abrir el paracaídas?
Solución
Aca se usa la ley de conservación de la energía para resolver el problema.
\[\begin{aligned} E_{c1}+E_{p1}+E_{E1}&=&E_{c2}+E_{p2}+E_{E2} \nonumber \\ 0+m\cdot g\cdot h_{1}+0&=&\frac{1}{2}mv^{2}+m\cdot g\cdot h_{2}+0 \nonumber \\ 0+ g\cdot h_{1}+0&=&\frac{1}{2}v^{2}+ g\cdot h_{2}+0 \nonumber \\ v&=&\sqrt{2g\left(h_{1}-h_{2}\right)} \nonumber \\ v&=&\sqrt{2\cdot9,8 m/s^{2}\left(4000m-1500m\right)}=221,39 m/s \end{aligned}\]
Exáctamente igual, pero ahora tenemos que calcular la altura a la cuál llegará a los 250 km/h.
\[\begin{aligned} E_{c1}+E_{p1}+E_{E1}&=&E_{c2}+E_{p2}+E_{E2} \nonumber \\ 0+m\cdot g\cdot h_{1}+0&=&\frac{1}{2}mv^{2}+m\cdot g\cdot h_{2}+0 \nonumber \\ 0+ g\cdot h_{1}+0&=&\frac{1}{2}v^{2}+ g\cdot h_{2}+0 \nonumber \\ h_{2}&=&\frac{g\cdot h_{1}-\frac{1}{2}v^{2}}{g} \nonumber \\ h_{2}&=&\frac{9,8m/s^{2}\cdot 4000m-\frac{1}{2}69,44 m/s}{9,8m/s^{2}}=3753,98m \end{aligned}\]
\(\blacksquare\)
Ejemplo 3.4. Sobre la cascada de un río se
coloca una turbina para generar energía eléctrica. Si la cascada tiene
una altura de 30 metros, y sabiendo que caen 250000 m\(^{3}\) por minuto, calcular la potencia que
entrega la turbina suponiendo que transforma el 53% de la energía
potencial en eléctrica.
Ayuda: recordar que la densidad del agua es 1000 kg/m\(^{3}\) y que se define como \(\rho=m/Vol\)
Solución
Acá hay que tener en cuenta que la energía es el trabajo realizado para calcular la potencia. Además debemos calcular la masa usando la densidad del agua.
\[\begin{aligned} P&=&\frac{E_{electrica}}{t} \nonumber \\ P&=&\frac{0,53 E_{p}}{t} \nonumber \\ P&=&\frac{0,53 \cdot mgh}{t} \nonumber \\ P&=&\frac{0,53 \cdot 250000000 kg \cdot 9,8m/s^{2}30m}{60s}=649250000 W =649,25 MW \\ \end{aligned}\]
\(\blacksquare\)
Ejercicios
Se dispara horizontalmente una bala de 55 g a corta distancia hacia adentro de un montículo de arena. La bala ingresa con una rapidez de 350 m/s y alcanza el reposo en la arena después de recorrer 18 cm. Determinar:
¿Cuál es la energía cinética inicial de la bala?
¿Qué fuerza promedio ejerce la arena sobre la bala?
Respuestas: 3369 J; -18715,28 N
Un cuerpo de masa 1 kg en caída libre tiene una velocidad de 10 m/s cuando esta a 80 m de altura.
¿Qué velocidad tendrá cuando esta a 20 m de altura?
¿Desde qué altura cayó suponiendo que la velocidad inicial es igual a cero?
Respuestas: 36 m/s; 85 m
Un cubo de hielo muy pequeño cae desprendido desde el borde de una cubetera semiesférica sin fircción y cuyo radio es de 23,6 cm. ¿A qué velocidad se mueve el cubo en el fondo de la cubetera?
Respuesta: 2,15 m/s
Una bola de 112 g es arrojada desde una ventana a una velocidad de 8,16 m/s y un ángulo de 34,0 grados sobre la horizontal. Usando la conservación de la energía determinar:
energía cinética de la bola en la parte más alta de su vuelo
su velocidad cuando está a 2,87m debajo de la ventana.
Despreciar la fuerza de arrastre del aire.
Respuesta: 2,56 J; 11,1 m/s
Una varilla delgada de longitud 2,13 m y de masa despreciable, está pivotada en un extremo de modo que pueda girar en circulo vertical. La varilla se separa en un ángulo de 35,0 grados y luego se suelta. ¿A qué velocidad se mueve la bola de plomo que está en el extremo de la varilla en su punto más bajo?
Respuesta: 2,75 m/s
Una piedra de 7,94 kg descansa sobre un resorte. El resorte se comprime 10,2 cm por la piedra.
Calcule la constante de fuerza del resorte
La piedra es empujada hacia abajo 28,6 cm más y luego se suelta. ¿Cuánta energía potencial hay almacenada en el resorte en el momento antes de que sea soltada la piedra?
¿A qué altura se elevará la piedra sobre esta nueva posición (la más baja)?
Por las cataratas del Niágara caen aproximadamente cada minuto 3,3\(\times 10^{5}\) m\(^{3}\) de agua, desde una altura de 50 m.
¿Cuál sería la salida de potencia de una planta generadora de electricidad que pudiera convertir el 48% de la energía potencial del agua en energía eléctrica?
Respuesta: 1300 MW
Un bloque de 1,93 kg se coloca contra un resorte comprimido sobre un plano inclinado de 27,0 grados son fricción. El resorte, cuya constante de fuerza es de 20,8 N/cm, se comprime 18,7 cm, después de lo cual el bloque se suelta. ¿Qué tanto subirá el bloque antes de alcanzar el reposo?
Respuesta: 4,24 m
Un bloque de 2,14 kg se deja caer desde una altura de 43,6 cm contra un resorte de constante de fuerza de 18,6 N/cm. Hallar la distancia máxima de compresión del resorte.
Respuesta: 9,9 cm
Una pequeña bola de acero de 1 kg está amarrada al extremo de un alambre de 1 m de longitud. El alambre se lo hace girar desde el otro extremo a una velocidad angular constante de 120 rad/s en circulos horizontales a 2,2 metros de altura
Calcular la energía cinética en el momento que la bola de acero está girando
Calcular la energía potencial que posee la bola cuando está girando
Si el alambre se corta, ¿con qué velocidad caerá la bola al piso? (Considerar unicamente la velocidad del eje vertical \(y\))
Calcular el trabajo efectuado por un hombre que arrastra un saco de harina de 65 kg por 10 m a lo largo del piso con una fuerza de 250 N y que luego lo levanta hasta un camión cuya plataforma está a 75 cm de altura. ¿Cuál es la potencia promedio desarrollada si el proceso entero tomó 2 minutos?
Ayuda: Tener en cuenta que para calcular la potencia hay que considerar el trabajo realizado por el hombre para arrastrar el saco y para luego levantarlo.
Impulso - Cantidad de Movimiento - Colisiones
Impulso y Cantidad de Movimiento
Definición 4.1. Impulso
Es el producto de la fuerza por el intervalo de tiempo que se aplica esa fuerza sobre el cuerpo.
\[\begin{aligned} I=F \cdot \Delta t \end{aligned}\]
Definición 4.2. Cantidad de Movimiento
Se define como el producto de la masa del cuerpo y su velocidad en un instante determinado.
\[\begin{aligned} CM=m \cdot \Delta v \end{aligned}\]
Ley de conservación de la cantidad de movimiento
Si tenemos un sistema de muchos cuerpos (por ejemplo dos), la cantidad de movimiento, en ausencia de fuerzas externas, se conserva.
\[\begin{aligned} m_{a} \cdot \Delta v_{a}+m_{b} \cdot \Delta v_{b}&=&0 \nonumber \\ m_{a} \cdot v_{a 1}+m_{b} \cdot v_{b 1}&=&m_{a} \cdot v_{a 2}+m_{b} \cdot v_{b 2} \end{aligned}\] donde el subíndice indica la partícula y el segundo subíndice distintos momentos del tiempo.
Ejemplo 4.1. Un cañón cuya masa es de 1300 kg
dispara una bala de 72 kg en dirección horizontal con una velocidad de
salida de 55 m/s. El cañón está montado de modo que pueda recular
libremente. ¿Cuál es la velocidad del cañón al recular con la salida de
la bala?
Solución
Usando la ley de conservación de la cantidad de movimiento tenemos,
\[\begin{aligned} m_{a} \cdot \Delta v_{a}+m_{b} \cdot \Delta v_{b}&=&0 \nonumber \\ m_{a} \cdot v_{a 1}+m_{b} \cdot v_{b 1}&=&m_{a} \cdot v_{a 2}+m_{b} \cdot v_{b 2} \nonumber \\ 0 + 0 &=& 1300 kg \cdot v + 72 kg \cdot 55 m/s \end{aligned}\]
Despejando \(v\),
\[\begin{aligned} v=-\frac{72 kg \cdot 55 m/s}{1300 kg}=-3,05 m/s \end{aligned}\]
\(\blacksquare\)
Colisiones
En una colisión, una fuerza relativamente grande actúa sobre cada
partícula que interviene en el choque durante un tiempo relativamente
corto. La idea básica de la colisión consiste en que el movimiento de
las partículas que colisionan (o al menos una de ellas), cambia de forma
brusca, y que podemos hacer una separación relativamente clara del
momento antes y después de la colisión.
En toda colisión siempre existe conservación del ímpetu o cantidad de
movimiento.
Colisiones elásticas
En una colisión elástica, además de la conservación de la cantidad de movimiento, también se conserva la energía cinética antes y después del choque. Es decir, en el caso de dos partículas tenemos:
\[\begin{aligned} \label{conservacion} m_{a} \cdot v_{a 1}+m_{b} \cdot v_{b 1}=m_{a} \cdot v_{a 2}+m_{b} \cdot v_{b 2} \end{aligned}\]
\[\begin{aligned} \label{cinetica_col} \frac{1}{2} m_{a} \cdot v_{a 1}^{2}+\frac{1}{2} m_{b} \cdot v_{b 1}^{2}=\frac{1}{2} m_{a} \cdot v_{a 2}^{2}+\frac{1}{2} m_{b} \cdot v_{b 2}^{2} \end{aligned}\]
Reescribiendo las ecuaciones [conservacion] y [cinetica_col] de la siguiente forma:
\[\begin{aligned} \label{conservacion2} m_{a} \cdot (v_{a 1}-v_{a 2})=m_{b} \cdot (v_{b 2}-v_{b 1}) \end{aligned}\]
\[\begin{aligned} \label{cinetica_col2} m_{a} \cdot (v_{a 1}^{2}-v_{a 2}^{2})=m_{b} \cdot (v_{b 2}^{2}-v_{b 1}^{2}) \end{aligned}\]
Descomponiendo la diferencia de cuadrados de la ecuación [cinetica_col2] tenemos:
\[\begin{aligned} \label{cinetica_col3} m_{a} \cdot (v_{a 1}-v_{a 2}) \cdot (v_{a 1}+v_{a 2})=m_{b} \cdot (v_{b 2}-v_{b 1}) \cdot (v_{b 2}+v_{b 1}) \end{aligned}\]
Ahora, dividiendo la ecuación [cinetica_col3] por la ecuación [conservacion2] tenemos:
\[\begin{aligned} \label{conservacion3} \frac{m_{a} \cdot (v_{a 1}-v_{a 2}) \cdot (v_{a 1}+v_{a 2})}{m_{a} \cdot (v_{a 1}-v_{a 2})}&=&\frac{m_{b} \cdot (v_{b 2}-v_{b 1}) \cdot (v_{b 2}+v_{b 1})}{m_{b} \cdot (v_{b 2}-v_{b 1})} \nonumber \\ v_{a 1}+v_{a 2}&=&v_{b 2}+v_{b 1} \end{aligned}\]
Entonces, si conoces las masas y las velocidades iniciales, podemos calcular las velocidades finales o velocidades después de la colisión.
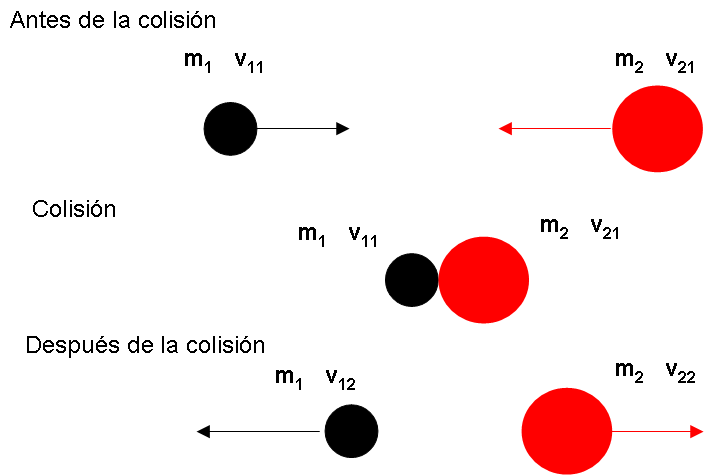 |
Combinando las ecuaciones [conservacion] y [conservacion3] y despejando para calcular las velocidades después del choque, se tiene que:
\[\begin{aligned} \label{ec_1} v_{a 2}=\frac{m_{a}-m_{b}}{m_{a}+m_{b}}\cdot v_{a 1}+\frac{2 m_{b}}{m_{a}+m_{b}}\cdot v_{b1} \end{aligned}\]
\[\begin{aligned} \label{ec_2} v_{b 2}=\frac{2 m_{a}}{m_{a}+m_{b}}\cdot v_{a1}+\frac{m_{b}-m_{a}}{m_{a}+m_{b}}\cdot v_{b1} \end{aligned}\]
Existen algunos casos particulares en los que se pueden aproximar las velocidades después del choque (ecuaciones [ec_1] y [ec_2]), siempre que se cumplan las condiciones planteadas (se omitirán las demostraciones):
Masas Iguales (\(m_{a}=m_{b}\)): En este caso las velocidades después del choque vienen dadas por:
\[\begin{aligned} v_{a2}&=&v_{b1} \\ v_{b2}&=&v_{a1} \end{aligned}\]
Partícula Blanco en Reposo (\(v_{b1}=0\)): La partícula blanco, a la cuál se impactará, la consideraremos a la segunda masa. Las velocidades finales para este caso son:
\[\begin{aligned} v_{a2}&=&\left(\frac{m_{a}-m_{b}}{m_{a}+m_{b}}\right)v_{a1} \\ v_{b2}&=&\left(\frac{2m_{a}}{m_{a}+m_{b}}\right)v_{a1} \end{aligned}\]
Blanco de masa muy grande (\(m_{b}\gg m_{a}\)): En este caso, la masa del blanco (\(m_{b}\)) es mucho más grande que la del proyectil (\(m_{a}\)), entonces las velocidades son:
\[\begin{aligned} v_{a2}&=&-v_{a1}+2v_{b1} \\ v_{b2}&=&v_{b1} \end{aligned}\]
Observar que en este caso la velocidad del blanco no cambia.
Proyectil de masa muy grande (\(m_{a}\gg m_{b}\)): En este caso, la masa del proyectíl (\(m_{a}\)) es mucho más grande que la del blanco (\(m_{b}\)), entonces las velocidades son:
\[\begin{aligned} v_{a2}&=&v_{a1} \\ v_{b2}&=&2v_{a1}-v_{b1} \end{aligned}\]
Observar que en este caso la velocidad del proyectil no cambia.
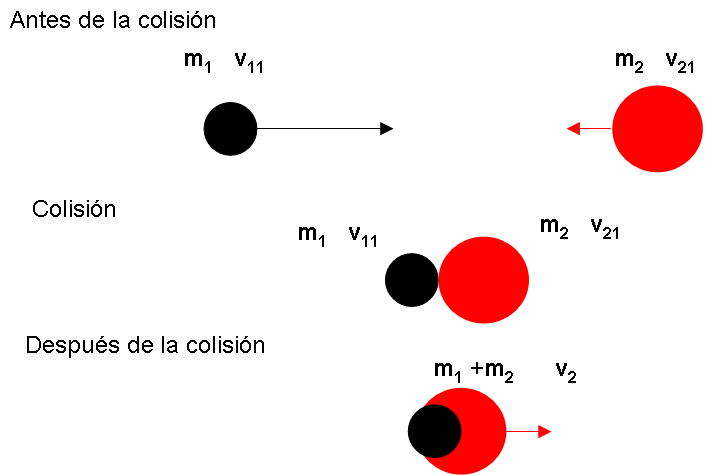
Colisiones inelásticas
En este caso, las partículas permanecen “pegadas” después de la
colisión, por ejemplo la colisión de una bala sobre un bloque de madera.
La conservación total de la energía se cumple, pero se añaden otras
energías distintas a la cinética, por lo que la ecuación [cinetica_col] no se cumple en este
tipo de choque.
En el caso especial de que el choque sea inelástico puro, entonces la
velocidad finales de las dos partículas es la misma, por lo que existe
una sola incógnita y la ecuación [conservacion] se transforma en:
\[\begin{aligned} m_{a} \cdot v_{a 1}+m_{b} \cdot v_{b 1}=\left( m_{a} +m_{b} \right) \cdot v_{2} \end{aligned}\]
 |
Ejemplo 4.2. Una bala de 3,8 g, se dispara
horizontalmente con una velocidad de 1100 m/s contra un gran bloque de
madera de masa igual a 12 kg que inicialmente está en reposo sobre una
mesa horizontal. Si el bloque puede deslizarse sin fricción por la mesa,
¿qué velocidad adquirirá después de que se le ha incrustado la
bala?
Solución
Usando la ley de conservación de la cantidad de movimiento y teniendo en cuenta que es un choque inelástico tenemos,
\[\begin{aligned} m_{a} \cdot v_{a 1}+m_{b} \cdot v_{b 1}&=&m_{a} \cdot v_{a 2}+m_{b} \cdot v_{b 2} \nonumber \\ 0 + 0,0038 kg \cdot 1100 m/s &=& 12 kg \cdot v + 0,0038 kg \cdot v \nonumber \\ 0 + 0,0038 kg \cdot 1100 m/s &=& \left( 12 kg + 0,0038 kg \right) v \end{aligned}\]
Despejando \(v\),
\[\begin{aligned} v=\frac{0,0038 kg \cdot 1100 m/s}{12 kg + 0,0038 kg}=0,35 m/s \end{aligned}\]
\(\blacksquare\)
Ejercicios
Dos bloques de 1,6 kg y otro 2,4 kg, se deslizan sin fricción con unas velocidades de 5,5 m/s y 2,5m/s en la misma dirección y sentido. Luego de la colisión, la velocidad del bloque mayor es de 4,9 m/s ¿Cuál es la velocidad del bloque de 1,6 kg después de la colisión? ¿Es una colisión elástica?
Respuesta: 1,9 m/s a la derecha
Un elefante furioso embiste a razón de 2,1 m/s contra una mosca que revolotea. Suponiendo que la colisión sea elástica, ¿a que velocidad rebota la mosca?
Respuesta: 4,2 m/s
Un carrito de 342g de masa se dirige sin fricción a una velocidad de 1,24 m/s contra otro carrito de masa desconocidad, que se encuentra en reposo, con el cuál colisiona. El choque entre los carritos es elástico. Después de la colisión, el primer carrito continúa con una velocidad de 0,636 m/s. ¿Cuál es la masa y la velocidad después del impacto del segundo carrito?
Se cree que el Meteor Crater, en Arizona, se formó por el impacto de un meteorito con la Tierra hace unos 20.000 años. La masa del meteorito se calcula que fue de \(5\times 10^{10}\) kg y su velocidad en 7,2 km/s. ¿Qué velocidad impartiría a la Tierra tal meteorito en una colisión frontal?
Un objeto de 2,0 kg de masa choca elásticamente contra otro objeto en reposo y continúa moviéndose en la dirección original pero a un cuarto de su velocidad inicial. ¿Cuál es la masa del objeto golpeado?
Respuesta: 1,2 kg
La cabeza de un palo de golf que se mueve a 45,0 m/s, golpea una pelota de golf (masa igual a 46,0 g) que descansa sobre el tee (punto donde se coloca la pelota). La masa efectiva de la cabeza del palo es de 230 g.
¿A qué velocidad deja el tee la bola?
¿A qué velocidad dejaría el tee si se duplicara la masa de la cabeza del palo?
¿Y si se triplicara?
¿Qué conclusiones puede sacarse de los palos pesados?
Supongase que las colisiones son perfectamente elásticas y que el golfista puede manejar los palos más pesados a igual velocidad en el impacto.
Respuesta: 74,4 ms; 81,8 m/s y 84,1 m/s
Un carro de carga del ferrocarril que pesa 35,0 toneladas (1000 kg) choca contra un furgón que está estacionado. Se acoplan entre sí y el 27% de la energía cinética inicial se disipa como calor, sonido y vibraciones. Halle el peso del furgón.
Solución
Planteando las ecuaciones de la cantidad de movimeinto para una colisión inelástica y la conservación de la energía cinética (teniendo en cuenta la pérdida de energía cinética como consecuencia del calor, sonido y vibraciones), tenemos:
\[\begin{aligned} m_{a} v_{a1} &=& \left(m_{a}+m_{b}\right) v_{2} \\ \frac{1}{2} \left(m_{a}+m_{b} \right) v_{2}^{2} &=& 0.73 \frac{1}{2}m_{a} v_{a1}^{2} \end{aligned}\]
Combinando ambas ecuaciones, se puede llegar a:
\[\begin{aligned} \frac{m_{a}}{m_{a}+m_{b}}&=&0,73 \\ m_{b}&=&12,9 \textbf{tn} \end{aligned}\]
\(\blacksquare\)
Un cañón de 3000 kg descansa sobre un estanque congelado. Se carga el cañón con una bala de 30 kg y se dispara de manera horizontal. Si el cañón retrocede hacia la derecha con una velocidad de 1,8 m/s. ¿Cuál es la velocidad de la bala del cañón inmediatamente después que es disparada?
Respuesta: -180 m/s
Un auto de masa 1800 kg se encuentra en reposo frente a un semáforo, en el momento que es colisionado por otro vehículo de masa 900 kg. Los autos quedan enredados después del choque. Se pide:
Si el segundo auto se mueve a 20 m/s antes del choque, ¿cuál será la velocidad de ambos autos después de la colisión?
¿Cuánta energía cinética se pierde en el choque?
Respuestas:‘6,67 m/s; 1,20\(\times 10^{5}\) J
Un objeto de 0,30 kg viaja con una velocidad de rapidez 2,0 m/s en la dirección positiva del eje \(x\) y tiene una colisión frontal elástica con otro cuerpo en reposo de masa 0,70 kg localizado en \(x=0\). ¿Cuál es la distancia que separa los cuerpos colisionados 25 s después del encuentro?
Respuesta: 50 m
Dinámica
Introducción
Hay tres conceptos que se usan todo el tiempo en dinámica. Estos conceptos son los de fuerza, masa y aceleración.
Definición 5.1 (Fuerza). En dinámica, vamos a considerar a la fuerza como un vector que hace que algo que está quieto se empiece a mover.
Cuando la fuerza empieza a actuar, el cuerpo que estaba quieto se
empieza a mover. Si uno no deja que el cuerpo se mueva, la fuerza
empieza deformarlo o romperlo.
Cuanto más masa tiene un cuerpo, más difícil es comenzar moverlo, y si
el cuerpo viene moviéndose, más difícil va a ser frenarlo. Entonces:
Definición 5.2 (Masa). La masa se define como una medida de la tendencia de los cuerpos al cambio de movimiento o inercia del cuerpo
De manera que la masa es una cantidad que me da una idea de qué tan difícil es acelerar o frenar a un cuerpo.
Definición 5.3 (Aceleración). La aceleración es una cantidad que me dice qué tan rápido está aumentando o disminuyendo la velocidad de un cuerpo.
Esto ya se sabe de cinemática. Digamos que si un objeto tiene una aceleración de \(10 m/s^{2}\), eso querrá decir que su velocidad aumenta en \(10 m/s\) por cada segundo que pasa. Si al principio su velocidad es cero, después de un segundo será de \(10 m/s\), después de 2 seg será de \(20 m/s\), etc.
Las unidades con la que se miden la Fuerza, la Masa y la Aceleración.
A la aceleración la vamos a medir en \(m/s^{2}\). (obviamente, igual que en cinemática). A la unidad \(m/s^{2}\) no se le da ningún nombre especial.
A la masa la medimos en Kilogramos. Recordemos que un kilogramo equivale a 1000 gramos.
A la fuerza la vamos a medir en dos unidades distintas: el Newton y el Kilogramo fuerza (kgf)
Un objeto que tiene un kilogramo de masa, ejerce un peso de un kilogramo fuerza. Un por el contrario, si un objeto tiene un kilogramo fuerza de peso, entonces tiene una masa de un kilogramo.
Masa y peso NO son la misma cosa, pero en La Tierra, una masa de 3 Kg pesa 3 Kgf La otra unidad de fuerza que se usa es el Newton. Un Newton es una fuerza tal que si uno se la aplica a un cuerpo que tenga una masa de 1 Kg, su aceleración será de 1 m/s\(^{2}\).
\(1 N = 1 Kg \times 1 m/s^{2}\) Por otra parte, la equivalencia entre \(Kgf\) y \(N\) viene dada por:
\(1 Kgf = 9,8 N\)
Leyes de Newton
Todo cuerpo permanece en su estado de reposo o de movimiento rectilíneo uniforme a menos que otros cuerpos actúen sobre él.
La sumatoria de las fuerzas que actúan sobre un cuerpo es directamente proporcional a su aceleración.
\[\begin{aligned} \sum{F}=m\cdot a \end{aligned}\]
Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza igual y de sentido opuesto.
Peso de un cuerpo
La fuerza con que La Tierra atrae a las cosas se llama Peso. Haciendo uso de la segunda ley de Newton se tiene:
\[\begin{aligned} F=m \cdot a \end{aligned}\]
Ahora, a la fuerza \(F\) la vamos a llamar Peso \(P\) y a la aceleración la denotaremos con \(g\), por ser la aceleración de la gravedad (\(9,8 m/s^2\)), entonces:
\[\begin{aligned} P=m \cdot g \end{aligned}\]
Por lo que podemos definir al peso como:
Definición 5.4 (Peso). El peso es la fuerza con la que la Tierra atrae a un objeto.
Aplicaciones
Los problemas se dinámica no son todos iguales. Pero en gran cantidad de ellos se pide calcular la tensión de la cuerda y la aceleración del sistema. Para ese tipo de problema hay una serie de pasos que conviene seguir
Hacer el diagrama de cuerpo libre para cada uno de los cuerpos que intervienen en el problema. Si hay un solo cuerpo, habrá un solo diagrama. Si hay 2 cuerpos habrá 2 diagramas, etc.
Un diagrama de cuerpo libre es un diagrama vectorial que describe todas las fuerzas que actúan sobre un cuerpo u objeto en particular. Consiste en colocar la partícula en el origen de un plano de coordenadas, y representar a las fuerzas que actúan sobre ella por medio de los vectores correspondientes, todos concurrentes en el origen.
La mayor aplicación de los diagramas de cuerpo libre es visualizar mejor el sistema de fuerzas que actúan sobre un cuerpo; además, se identifican mejor las fuerzas pares, como la de acción - reacción y las componentes de las fuerzas.
Si en un sistema existen dos o más cuerpos de interés, éstos se deben separar y cada uno tiene un diagrama propio con sus respectivas fuerzas actuando.
De acuerdo al diagrama de cuerpo libre, planteo la 2ª ley de Newton:
\[\begin{aligned} \sum{F}=m\cdot a \end{aligned}\]
Para cada diagrama de cuerpo libre voy a tener una ecuación. De la ecuación (o sistema de ecuaciones) se calcula la incógnita en cuestión.
Este método para resolver problemas de dinámica sirve para cualquier tipo de problema, sea con rozamiento, sin rozamiento, plano horizontal, plano inclinado, etc.
Fuerzas de Fricción o Rozamiento
Si lanzamos un bloque de masa \(m\)
a una velocidad inicial \(v_{0}\) a lo
largo de una mesa horizontal larga, al final llegará al reposo. Esto
significa que mientras se está moviendo experimenta una aceleración
promedio que apunta en dirección contraria al movimiento. En este caso
afirmamos que la mesa ejerce una fuerza de fricción sobre el bloque,
cuyo valor viene dado por la segunda ley de Newton.
La fuerza de fricción es directamente opuesta al movimiento relativo del
objeto.
Por otra parte, las fuerzas de fricción que actúan sobre superficies
estáticas, se llaman fuerzas de fricción estáticas. Una
vez que se ha iniciado el movimiento, las fuerzas de fricción que actúan
sobre las superficies de los cuerpos generalmente disminuyen, de manera
que sólo es necesario una fuerza más pequeña para mantener un movimiento
uniforme (velocidad constante). Las fuerzas que actúan sobre superficies
en movimiento, se llaman fuerzas de fricción
dinámica.
La fuerza de fricción es proporcional a la fuerza normal que ejerce el
cuerpo sobre la superficie y es aproximadamente independiente del área
de contacto.
Si \(f_{e}\) representa la magnitud de
la fuerza de fricción estática, podemos escribir:
\[\begin{aligned} f_{e}=\mu_{e} N \end{aligned}\] donde \(\mu_{e}\) es el coeficiente de fricción estático y \(N\) es la magnitud de la fuerza normal.
La fuerza de fricción dinámica \(f_{d}\) entre superficies secas no lubricadas, sigue las mismas leyes que la fuerza de fricción estática. Si \(f_{d}\) representa la magnitud de la fuerza de fricción dinámica, podemos escribir:
\[\begin{aligned}
f_{d}=\mu_{d} N
\end{aligned}\] donde \(\mu_{d}\) es el coeficiente de fricción
dinámica.
Tanto \(\mu_{e}\) como \(\mu_{d}\) son constantes sin dimensión,
cuyos valores dependen de la naturaleza de los cuerpos. Siempre se
cumple que \(\mu_{e}>\mu_{d}\).
Ejemplo 5.1. Un cuerpo de masa 5 kg se mueve con
velocidad 10 m/s por una zona con rozamiento. Suponiendo que el \(\mu_{d}=0,3\), calcular la aceleración que
hace frenar al cuerpo.
Solución
El diagrama de cuerpo libre en este caso va a ser:
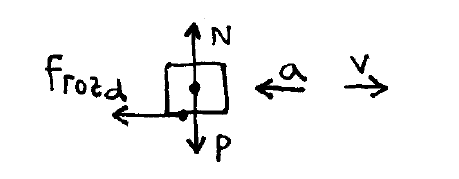 |
Planteando que la segunda ley de Newton sobre el eje \(x\) tenemos que:
\[\begin{aligned} \sum{F}_{x}&=&m\cdot a \nonumber \\ f_{c}&=& m\cdot a \nonumber \\ \mu_{d} N&=& m\cdot a \end{aligned}\]
Teniendo en cuenta que en este caso la magnitud de la fuerza normal coincide con el peso, y sabiendo que \(P=m\cdot g\), podemos escribir:
\[\begin{aligned} \mu_{d} P&=& m\cdot a \nonumber \\ \mu_{d} m \cdot g&=& m\cdot a \nonumber \\ \mu_{d} g&=& a \nonumber \\ a&=&9,8 m/s^{2} \cdot 0,3 \nonumber \\ a&=&2,94 m/s^{2} \end{aligned}\]
\(\blacksquare\)
Plano Inclinado
Supongamos que tenemos un cuerpo que está apoyado en un plano que está inclinado un ángulo \(\alpha\). Entonces, la fuerza peso apunta para abajo de esta manera:
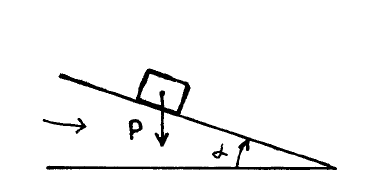 |
Para resolver este tipo de problema, hay que descomponer el peso en las direcciones de los ejes cartesianos, que en este caso hay que orientar la dirección del eje \(x\) paralela al plano inclinado, y el eje \(y\) perpendicular a éste. Gráficamente,
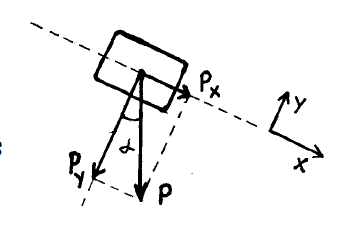 |
donde se puede verificar por simple trigonométría que el ángulo \(\alpha\) es el mismo ángulo que tiene ek plano inclinado. Por lo que, la descomposición de las fuerzas que intervienen en el diagrama de cuerpo libre, utilizando los ejes cartesianos propuestos, toma la forma:
\[\begin{aligned} \sum{F_{x}}&=&m \cdot a_{x} \nonumber \\ P_{x}=&=&m \cdot a_{x} \nonumber \\ P \cdot \sin{\alpha}=&=&m \cdot a_{x} \\ \sum{F_{y}}&=&m \cdot a_{y} \nonumber \\ N-P_{y}=&=&m \cdot a_{y} \nonumber \\ N-P \cdot \cos{\alpha}=&=&m \cdot a_{y} \end{aligned}\]
En el caso de existir rozamiento entre el cuerpo y el plano inclinado, esta fuerza estará en la dirección del eje \(x\) y tendrá un sentido opuesto al movimiento del cuerpo, por lo qe las ecuaciones tomarán la siguiente forma:
\[\begin{aligned} P \cdot \sin{\alpha}-f_{d}=&=&m \cdot a_{x} \\ N-P \cdot \cos{\alpha}=&=&m \cdot a_{y} \end{aligned}\]
En el caso de que el cuerpo no se encuentre en movimiento, es decir esté en reposo, las ecuaciones se pueden sintetizar de la siguiente manera:
\[\begin{aligned} P \cdot \sin{\alpha}-f_{e}=&=&0 \\ N-P \cdot \cos{\alpha}=&=&0 \end{aligned}\] dado que las aceleraciones en ambos ejes son nulas.
Ejemplo 5.2. Un bloque está en reposo sobre un
plano inclinado que forma un ángulo \(\alpha\) con la horizontal. Cuando el
ángulo se eleva por encima de los 15º empieza el desplazamiento.
Calcular el coeficiente de fricción estático.
Solución
Teniendo en cuenta que el cuerpo se encuentra en reposo, por lo que la segunda ley de Newton es igualada a cero, es decir \(\sum{F}=0\), y resolviendo las fuerzas que actúan en las componentes \(x\) e \(y\) (a lo largo del plano inclinado y normal al plano, respectivamente), obtenemos:
\[\begin{aligned} \sum{F_{x}}&=&P \cdot \sin{\alpha}-f_{d}=0 \\ \sum{F_{y}}&=&N-P \cdot \cos{\alpha}=0 \end{aligned}\]
Suponiendo que el ángulo \(\alpha\) corresponde al ángulo justo antes de que el bloque comience su desplazamiento, y reordenando las ecuaciones, tenemos que:
\[\begin{aligned} P \cdot \sin{\alpha}&=&f_{d} \\ P \cdot \cos{\alpha}&=&N \end{aligned}\]
Dividiendo ambas ecuaciones, se puede llegar a:
\[\begin{aligned} \frac{P \cdot \sin{\alpha}}{P \cdot \cos{\alpha}}&=&\frac{f_{d}}{N} \end{aligned}\]
Pero como \(f_{d}=\mu_{d} N\), entonces:
\[\begin{aligned} \mu_{d}=\tan{\alpha}=\tan{15º}=0,27 \end{aligned}\]
Como conclusión, la medición del ángulo de un plano inclinado puede ser usado como un experimento para medir el coeficiente de fricción estático entre dos superficies. Por otra parte, cabe destacar que el coeficiente de fricción no depende del peso del cuerpo.
\(\blacksquare\)
Ejemplo 5.3. Consideremos un auto que se
desplaza a lo largo de una ruta recta horizontal con una velocidad
inicial de 72 km/h. Suponiendo que el coeficiente de fricción dinámico
entre las llantas y el pavimento es de 0,23, calcular la distancia más
corta en que puede ser detenido el auto sin utilizar los frenos.
Solución
Sabiendo que es un movimiento rectilíneo uniformemente variado, y haciendo uso de la relación [mruv_rel]
\[\begin{aligned} v_{2}^{2}-v_{1}^{2}&=&2 a \Delta x \end{aligned}\]
Eligiendo una posición inicial \(x_{1}=0\) y suponiendo que el auto se detuvo (\(v_{2}=0\)), entonces se puede llegar a:
\[\begin{aligned} \label{din1} x_{2}&=&-\frac{v_{1}^{2}}{2a} \end{aligned}\]
Para determinar el valor de \(a\) usaremos la segunda ley de Newton, donde:
\[\begin{aligned} \sum{F_{x}}&=&-f_{d}=m \cdot a_{x} \\ \sum{F_{y}}&=&N-P \cdot \cos{\alpha}=0 \Rightarrow N=mg \end{aligned}\]
Haciendo uso de la definición de la fuerza de fricción, tenemos que:
\[\begin{aligned} f_{d}=\mu_{d} N = \mu_{d} m \cdot g \end{aligned}\] por lo que reemplazando en la ecuación del eje \(x\) y despejando \(a\), se tiene:
\[\begin{aligned} a=-\mu_{d} g \end{aligned}\]
Sustituyendo en el valor de la aceleración en la ecuación [din1], se llega a:
\[\begin{aligned} x_{2}&=&-\frac{v_{1}^{2}}{2a}=\frac{v_{1}^{2}}{2\mu_{d} g}=\frac{(20m/s)^{2}}{2\cdot 0,23 \cdot 9,8m/s^{2}}=88,7 m \end{aligned}\]
Cabe destacar que:
Cuanto mayor es la velocidad inicial, mayor será la distancia requerida para frenar. Más aún, esta distancia varía con el cuadrado de la velocidad.
Cuanto más grande sea el coeficiente de fricción, menor será la distancia requerida para frenar el auto.
\(\blacksquare\)
Ejercicios
A un cuerpo de masa m=10Kg se le aplica una fuerza horizontal F=40 N si el coeficiente de rozamiento es \(\mu_{d}=0,1\) calcular
La acelaración
Espacio recorrido a los 5 segundos.
Se arrastra un cuerpo de masa m=25 Kg por una mesa horizontal , con una fuerza F=80 N que forma un angulo de 60 grados y coeficiente de rozamineto \(\mu_{d}=0,1\) calcular :
La acelaración
Velocidad a los 3 segundos.
Un cuerpo de masa m=80 kg que se mueve a una velocidad de 20 m/s se para después de recorrer 50 m en un plano horizontal con rozamiento. Calcula \(\mu_{d}\).
Calcular la aceleración del sistema de la figura y la tensión en la cuerda, suponiendo que \(m_{A}=10 kg\), \(m_{B}=5kg\) y \(\mu_{d}=0,2\).
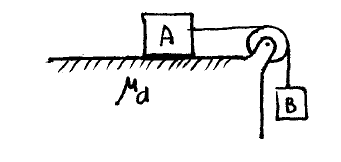
Una grúa eleva una masa m=800 kg mediante un cable q soporta una tensión de 12000 N
¿Cuál es la máxima aceleración con que se puede elevar?
Si se eleva con una a=2 \(m/s^{2}\) ¿que tensión soporta el cable?
Sobre una superficie horizontal se desliza un cuerpo de masa m=12Kg mediante una cuerda que pasa por una polea fija y lleva colgado del otro extremo una masa m= 8 Kg . Si \(\mu_{d}=0,1\). Calcular:
Aceleración del sistema
Tensión de la cuerda
Se quiere subir un cuerpo de masa m= 5 kg por un plano inclinado de ángulo de inclinación 30º y con un coeficiente de rozamiento dinámico de 0,2 mediante la aplicación de una fuerza paralela al plano inclinado F=45 N. Calcular la aceleración del cuerpo.
Si el coeficiente de rozamiento estático entre la masa y el plano inclinado es 0,4. ¿Cuál será ángulo de inclinación del plano?
Calcular la masa de un cuerpo que al recibir una fuerza de 20 N adquiere una aceleración de \(5 m/s^{2}\).
Un cuerpo de 15 kg se encuentra sobre una superficie horizontal. Calcula los coeficientes de rozamiento estático y dinámico si hay que aplicar paralelamente a dicho plano una fuerza de 51,45 N para que comience a deslizarse y otra de 36,75 N para que mantenga un MRU.
A lo largo de una rampa inclinada 30º sobre la horizontal se sube una carretilla de 10 kg de masa aplicándole una fuerza de 100 N paralela a la rampa. Si el coeficiente dinámico de rozamiento es de \(\mu_{d}= 0,5\), hacer un esquema detallando las fuerzas que actúan y calcula:
La fuerza normal que ejerce la superficie.
La fuerza de rozamiento.
Calcula la aceleración con la que sube la carretilla.
Fluidos
Sin entrar en demasiado detalle, vamos a distinguir entre un fluido y
un sólido con la siguiente característica:
El sólido conserva su forma, pero el fluido fluye para adoptar la
forma del recipiente
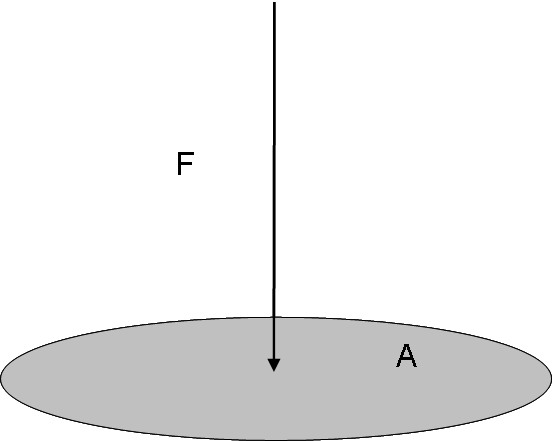
Definición 6.1. Presión
La magnitud de la fuerza normal por unidad de área superficial se llama presión, es decir:
\[\begin{aligned} P=\frac{F}{A} \end{aligned}\]
La unidad con la que se mide la presión es el Pascal y equivale a N/m\(^{2}\).
 |
Ejemplo 6.1. Supongamos un cuerpo C que ejerce,
sobre la superficie que ocupa, una fuerza vertical igual a 500 N que es
en este caso, su peso. Si la superficie de la base es 33 cm\(^{2}\), el peso se repartirá en toda ella.
¿Cuál será la presión que se ejerce?
Solución
\[\begin{aligned} P=\frac{F}{A}=\frac{500 N}{0,0033 m^{2}}=151515,1 Pa \end{aligned}\]
\(\blacksquare\)
Definición 6.2. Densidad
La densidad se define como la masa de un elemento divido por el volumen que dicho elemento ocupa.
\[\begin{aligned} \rho=\frac{m}{V} \end{aligned}\]
Presión de un Fluido en Reposo
Consideremos un fluido que está en equilibrio, entonces la relación que nos dice como varía la presión con la elevación sobre cierto nivel de referencia viene dado por:
\[\begin{aligned} P_{2}-P_{1}=\rho g \left( h_{2}-h_{1} \right) \end{aligned}\]
Si el fluido tiene una superficie libre, entonces la presión \(P_{1}\) es ejercida por la atmósfera de la Tierra, por lo que se puede escribir:
\[\begin{aligned} P=P_{0}+\rho g h \end{aligned}\]
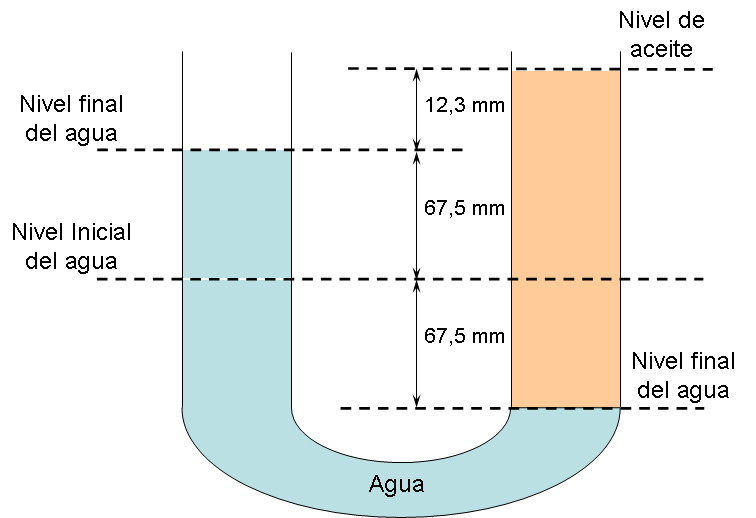
Ejemplo 6.2. Un tubo en U, en el cual ambos
extremos están abiertos a la atmósfera, contiene cierta cantidad de
agua. En el otro lado se vierte aceite, sustancia que no se mezcla con
el agua, hasta llegar a una distancia de \(d=12,3 mm\) sobre el nivel del agua, del
otro lado, nivel que se ha elevado mientras tanto a una distancia de
\(a=67,5 mm\) desde su nivel original.
Hallar la densidad del aceite en el punto mas bajo del agua (unión de
aceite y agua).
 |
Solución
Igualando las presiones de cada uno de los lados del tubo en forma de U, tenemos que:
\[\begin{aligned} P_{0}+\rho_{agua} \cdot 2a&=&P_{0}+\rho_{aceite} \cdot \left(2a+d\right) \nonumber \\ \rho_{aceite}&=&1000 kg/m^{3} \frac{2\left(67,5 mm\right)}{2\left(67,5 mm\right)+12,3 mm} \end{aligned}\]
\(\blacksquare\)
Principio de Pascal
La presión aplicada a un fluido confinado se transmite
íntegramente a todas las partes del fluido y a las paredes del
recipiente que lo contiene.
Es decir, si aumentamos la presión en alguna parte del fluido, cualquier
otra parte del fluido experimenta el mismo aumento de presión.
\[\begin{aligned} \frac{F_{1}}{A_{1}}=\frac{F_{2}}{A_{2}} \end{aligned}\]
Ejemplo 6.3. Gato hidráulico empleado para
elevar un auto. Se emplea una bomba de mano, con la cuál se aplica una
fuerza al émbolo menor de 2,2 cm de diámetro. La masa combinada del auto
que va a ser elevado con la plataforma de elevación es de 1980 kg, y el
émbolo grande tiene 16,4 cm de diámetro. Calcular la fuerza necesaria
para elevar el auto.
Solución
Usando el principio de Pascal,
\[\begin{aligned} \frac{F_{1}}{A_{1}}&=&\frac{F_{2}}{A_{2}} \nonumber\\ F_{1}&=&m \cdot g \frac{A_{1}}{A_{2}} \nonumber\\ F_{1}&=&1980 kg \cdot 9,8 m/s^{2} \frac{\pi \left( 1,1 cm \right)^{2}}{\pi \left( 8,2 cm \right)^{2}} \nonumber\\ F_{1}&=&349 N \end{aligned}\]
\(\blacksquare\)
Principio de Arquímides
Todo cuerpo total o parcialmente sumergido en un fluido sufre un empuje de abajo hacia arriba por una fuerza de magnitud igual al peso del fluido que desaloja.
Ejemplo 6.4. ¿Que fracción del volumen total de
un iceberg queda expuesta?
Solución
El peso del iceberg es:
\[\begin{aligned} W=\rho_{i} V_{i} g \end{aligned}\] donde \(V_{i}\) es el volumen del iceberg. El peso del volumen del agua desalojada es la fuerza de flotación, es decir:
\[\begin{aligned} F_{b}=\rho_{agua} V_{d} g \end{aligned}\]
Pero \(F_{b}\) es igual a \(W\) porque el iceberg está en equilibrio, por lo que:
\[\begin{aligned} \rho_{i} V_{i} g=\rho_{agua} V_{d} g \end{aligned}\]
Usando las densidades del agua de mar (1024 kg/m\(^{3}\)) y del hielo (917 kg/m\(^{3}\)),
\[\begin{aligned} \frac{V_{d}}{V_{i}}=\frac{\rho_{i}}{\rho_{agua}}=\frac{917 kg/m^{3}}{1024 kg/m^{3}}=0,896=89,6\% \end{aligned}\]
\(\blacksquare\)
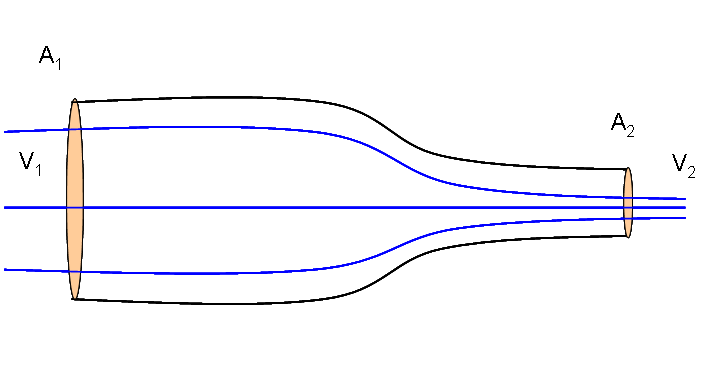
Ecuación de Continuidad
Supongamos un fluido entra en un tubo por uno de los lados con mayor diámetro y sale por el otro lado, el cual tiene menor diámetro. Además, se supone que entre los dos extremos del tubo no puede ni entrar ni salar fluido, y que el fluido tiene densidad constante. Entonces,
\[\begin{aligned}
A_{1}v_{1}=A_{2}v_{2}
\end{aligned}\] donde \(A\) es
el área de cada uno de los extremos del tubo y \(v\) es la velocidad del fluido al pasar por
cada uno de los extremos respectivamente. El producto del área por la
velocidad también es llamado razón de flujo volumétrico.
 |
La razón de flujo volumétrico también puede ser escrita como:
\[\begin{aligned} R=A\cdot v=\frac{Volumen}{t} \end{aligned}\]
Ejemplo 6.5. Un grifo cuya corriente de agua se
angosta desde un área de 1,2 cm\(^{2}\)
hasta los 0.35 cm\(^{2}\). Los dos
niveles donde se miden las áreas están separados 45 mm. ¿En qué cantidad
fluye el agua de la llave?
Solución
\[\begin{aligned} A_{1}v_{1}=A_{2}v_{2} \end{aligned}\]
Teniendo en cuenta la ecuación [mru_v], se puede escribir:
\[\begin{aligned} v_{2}^{2}=v_{1}^{2}+2 \cdot gh \end{aligned}\]
Eliminando la \(v_{2}\) y resolviendo para \(v_{1}\), se tiene:
\[\begin{aligned} v_{1}&=&\sqrt{\frac{2ghA_{2}^{2}}{A_{1}^{2}-A_{2}^{2}}} \nonumber \\ &=&28,6 cm/s \end{aligned}\]
Luego, la razón de flujo volumétrico viene definida como:
\[\begin{aligned} R=A_{1}v_{1}=1,2 cm^{2} \cdot 28,6 cm/s=34 cm^{3}/s \end{aligned}\]
\(\blacksquare\)
Ecuación de Bernoulli
La ecuación de Bernoulli es una relación fundamental en la mecánica de los fluidos y se deriva de las leyes de la mecánica de Newton. Omitiendo la demostración de como se deriva la ecuación, tenemos:
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho g y_{1}=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho g y_{2} \end{aligned}\]
Ejemplo 6.6. Un tanque elevado de altura \(h=32\) m y diámetro \(D=3,0\) m, abastece de agua una casa. Una
tubería horizontal en la base del tanque tiene un diámetro de \(d=2,54\) cm. Para satisfacer las
necesidades del hogar, la tubería de abastecimiento debe ser capaz de
sustituir agua a razón de \(R=0,0025\)
m\(^{3}\)/s. Si el agua estuviese
fluyendo a la cantidad máxima, ¿cuál sería la presión en la tubería
horizontal?
Solución
Aplicando la ecuación de Bernoulli, tenemos:
\[\begin{aligned} P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho g y_{1}=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho g y_{2} \end{aligned}\]
En \(1\), la presión es la atmosférica (parte superior del tanque). Con \(y_{1}=h\) y \(y_{2}=0\), obtenemos:
\[\begin{aligned} P_{atm}+\frac{1}{2}\rho v_{1}^{2}+\rho g h&=&P_{2}+\frac{1}{2}\rho v_{2}^{2} \nonumber \\ P_{2}&=&P_{atm}+\frac{1}{2}\rho \left(v_{1}^{2}-v_{2}^{2}\right)+\rho g h \end{aligned}\]
Por otro lado, podemos hallar las velocidades a partir de la igualdad del flujo volumétrico, es decir:
\[\begin{aligned} R&=&A_{1}v_{1}=A_{2}v_{2} \nonumber \\ v_{1}&=&\frac{R}{A_{1}}=3,5 \times 10^{-4} m/s \nonumber \\ v_{2}&=&\frac{R}{A_{2}}=4,9 m/s \end{aligned}\]
Entonces,
\[\begin{aligned} P_{2}&=&P_{atm}+\frac{1}{2}\rho \left(v_{1}^{2}-v_{2}^{2}\right)+\rho g h\\ &=& 101325 Pa+\frac{1}{2} 1000 kg/m^{3} \left(1,16 \times 10^{-7} m^{2}/s^{2}-24,01 m^{2}/s^{2}\right)+\\ & &+1000 kg/m^{3} 9,8 m/s^{2} 32m\\ &=&4,03 \times 10^{5} Pa \end{aligned}\]
\(\blacksquare\)
Ejercicios
Supongamos que tenemos una cama de agua que mide 2 m de lado y 30 cm de profundidad, teniendo en cuenta que la densidad del agua es igual a 1000 kg/m\(^{3}\). ¿Cuál será el peso de la cama de agua? Exprese el resultando en Newton.
Respuesta: 11760 N
El tubo de entrada que suministra aire a presión para que funcione un elevador hidráulico tiene 5 cm de diámetro. El émbolo de salida tiene un diámetro de 44 cm. ¿Cuál será la presión que debe utilizarse para elevar un automóvil que pesa 2300 kg?
Respuesta:
Se desea construir un elevador hidráulico para ejercer fuerzas de 12000 N. ¿Cuál debería ser el área del pistón grande, si sobre el menor, que es de 20 cm\(^{2}\) de área, se aplica una fuerza de 80 N?
Respuesta:
Por un conducto recto, circula agua a una velocidad de 25 m/seg. Si la sección del tubo es de 8 cm\(^{2}\). ¿Cuál es el caudal circulante de la corriente de agua?
Respuesta:
Por un conducto que tiene 15 cm\(^{2}\) de sección, circula agua a razón de 50 cm/s. ¿Cuál será el volumen de agua que pasó en 55 segundos?
Respuesta:
Un tubo de 34,5 cm de diámetro conduce agua que circula a razón de 2,62 m/s. ¿Cuánto tiempo le tomará descargar 1600 m\(^{3}\) de agua?
Respuesta: 49 min
A veces se prueban modelos de torpedos en un tubo horizontal por el que fluye agua, muy similar al túnel de viento que se emplea para probar modelos de aeroplanos. Considere un tubo circular de 25,5 cm de diámetro interno y un modelo de torpedo alineado a lo largo del eje del tubo, con un diámetro de 4,80 cm. El torpedo va a ser probado con el agua que circula a razón de 2,76 m/s. Calcular:
¿A qué velocidad deberá fluir el agua en la parte no reducida del tubo?
Hallar la diferencia de presión entre la parte no reducida y la reducida del tubo.
Respuesta: 2,66 m/s; 271 Pa
Las ventanas de un edificio de oficina tienen 4,26 m por 5,26 m. En un día tempestuoso, el aire sopla a razón de 28,0 m/s al pasar por una ventana en el piso 53. Calcule la fuerza neta sobre la ventana. La densidad del aire es de 1,23 kg/m\(^{3}\)
Respuesta: 10800 N
Termodinámica
Temperatura
Definición 7.1. Temperatura
Existe una cantidad escalar, llamada temperaturam, que es una propiedad de todos los sitemas termodinámicos en equilibrio. Dos sistemas están en equilibrio térmico sí y sólo si sus temperaturas son iguales
Medición de la Temperatura
La temperatura y una de las siete unidades básicas (las otras
unidades son longitud, tiempo, masa, intensidad de corriente eléctrica,
cantidad de sustancia e intensidad luminosa).
Las escalas Celsius y Fahrenheit
En casi todos los países del mundo se emplea la escala Celsius. La
escala Celsius se basó originalmente en dos puntos de calibración, el
punto de cengelación del agua que se definió en cero grado, y el punto
de ebullición del agua, que se definió en 100 grados. Estos dos puntos
se emplearon para calibrar termómetros, y luego se dedujeron las demás
temperaturas por interpolación y extrapolación.
La escala Fahrenheit, originalmente también se basó en dos puntos: el
punto de congelación de una mezcla de agua y sal, y la temperatura media
del cuerpo humano. En esta escala, los puntos de congelamiento y
ebullición del agua son 32ºF y 212ºF respectivamente.
\[\begin{aligned} T_{F}=\frac{9}{5}T_{C}+32 \end{aligned}\]
Escala Kelvin
Para la calibración de esta escala, se escogió el punto triple del
agua, que es la temperatura en la que coexisten el gua, el hielo y
el vapor, el cuál es muy cercano al punto de congelación del agua.
\[\begin{aligned} T_{C}=T-273,15 \end{aligned}\]
Capacidad Calorífica en los Sólidos
Definición 7.2. Calor
El calor es energía que fluye entre un sistema y su entorno en virtud de
una diferencia de temperatura entre ellos.
Ya que el calor es una forma de energía, sus unidades son las de la energía. La unidad que se suele usar para medir el calor es la caloría, donde:
\[\begin{aligned} 1 \quad \textbf{cal}=4,186 J \end{aligned}\]
La cantidad de calor que se transmite por cada grado de temperatura que se aumenta, se puede calcular como:
\[\begin{aligned} Q=m C_{e}\left(T_{f}-T_{i}\right) \end{aligned}\] donde \(C_{e}\) es el calor específico una característica propia de cada material o sustancia que compone el cuerpo, \(m\) la masa del cuerpo, y \(T_{i}\) y \(T_{f}\) son las temperaturas iniciales y finales respectivamente. Las unidades que se mide generalmente el calor específico son \(\textbf{cal}/g ºC\).
Definición 7.3. Capacidad
Calorífica
Es el calor específico multiplicado por la masa del cuerpo, es
decir:
\[\begin{aligned} C= C_{e}m \end{aligned}\]
La capacidad calorífica es característica de un objeto en particular, a diferencia del calor específico que carecteriza a la sustancia.
Principio Cero de la Termodinámica
| En un sistema aislado, la cantidad de calor es igual a cero. Es decir, si un objeto cede |
| calor (negativo), el otro objeto lo absorve (positivo). En otras palabras, |
| \(Q_{absorvido}=Q_{cedido}\quad\) ó bien \(\quad \sum Q=0\) |
Ejemplo 7.1. Una muestra de cobre, cuya masa es
de 75g se calienta en una estufa de laboratorio a una temperatura de
312ºC. El cobre se deja luego caer en un vaso que contiene agua (masa de
220g) a una temperatura de 12ºC. ¿Cuál es la temperatura final del cobre
y del agua luego de que llegan al equilibrio?
Solución
Partiendo que la energía que sale de un objeto en un sistema aislado es absorvida por otro objeto, entonces tenemos que:
\[\begin{aligned} & &\sum Q=0 \nonumber \\ & &Q_{agua}+Q_{cobre}=0 \nonumber \\ & &m_{agua} C_{e}^{agua} \left(T_{f}-T_{i}^{agua}\right)+m_{cobre} C_{e}^{cobre} \left(T_{f}-T_{i}^{cobre}\right)=0 \nonumber \\ & &220g\cdot 1 \textbf{cal}/g ºC \left(T_{f}- 12ºC\right)+75g\cdot 0,092 \textbf{cal}/g ºC \left(T_{f}- 312ºC\right)=0 \end{aligned}\]
Despejando \(T_{f}\) tenemos:
\[\begin{aligned} T_{f}=\frac{220g\cdot 1 \textbf{cal}/g ºC \cdot 12ºC+75g\cdot 0,092 \textbf{cal}/g ºC \cdot 312ºC}{220g\cdot 1 \textbf{cal}/g ºC+75g\cdot 0,092 \textbf{cal}/g ºC}=21,12°C \end{aligned}\]
\(\blacksquare\)
Calores de Transformación
Cuando entra calor a un sólido o líquido, la temperatura de la
muestra no se eleva necesariamente. En cambio, la muestra puede cambiar
de una fase o estado (sólido, líquido o gaseoso) a otro. Por lo tanto,
el hielo se funde, y el agua hierve, absorviendo calor en cada caso sin
un cambio de temperatura. En los precesos inversos (el agua se congela y
el valor se condensa), la muestra libera calor a una temperatura
constante.
La cantidad de calor por unidad de masa transferido durante un cambio de
fase, se llama calor de transformación, y se
calcula como:
\[\begin{aligned} Q=L \cdot m \end{aligned}\] donde \(m\) es la masa de la muestra en cada fase y \(L\) es un valor que depende de la sustancia y de la fase. A continuación se presenta una tabla con algunos valores de \(L\) para distintas sustancias:
| Sustancia | Punto de fusión | Calor de fusión | Punto de ebullición | Calor de vaporización |
| (K) | (kJ/kg) | (K) | (kJ/kg | |
| Hidrógeno | 14,0 | 58,6 | 20,3 | 452,0 |
| Oxígeno | 54,8 | 13,8 | 90,2 | 213,0 |
| Mercurio | 234,0 | 11,3 | 630 | 296,0 |
| Agua | 273,0 | 333,0 | 373,0 | 2256,0 |
| Plomo | 601,0 | 24,7 | 2013,0 | 858,0 |
| Plata | 1235,0 | 105,0 | 2485,0 | 2336,0 |
| Cobre | 1356,0 | 205,0 | 2840,0 | 4730,0 |
Ejemplo 7.2. Una persona prepara una cantidad de
té helado mezclando 520 g de té caliente (esencialmente agua) con una
masa igual de hielo a 0ºC. ¿Cuáles son la temperatura final y la masa de
hielo restante si el té caliente está inicialmente a una temperatura de
a) 70ºC y b) 90ºC?
Solución
Vamos a suponer que el hielo se derrite completamente y calcularemos la temperatura de equilibrio del sistema, entonces podemos escribir:
\[\begin{aligned} \label{ej_calor} & &\sum Q=0 \nonumber \\ & &Q_{agua}+Q_{\textbf{fusión del hielo}}+Q_{agua derretida}=0 \nonumber \\ & &m_{agua}\cdot C_{e}\left(T_{f}-T_{i}^{agua}\right)+m_{hielo}\cdot L+m_{hielo} \cdot C_{e}\left(T_{f}-T_{i}^{hielo}\right)=0\nonumber \\ & &0,52kg \cdot 4,186 kJ/kg ºC \cdot \left(T_{f}-70ºC\right)+0,52 kg \cdot 333 kJ/kg+\nonumber \\ & &+0,52kg \cdot 4,186 kJ/kg ºC \cdot \left(T_{f}-0ºC\right)=0 \end{aligned}\]
Despejando \(T_{f}\) tenemos:
\[\begin{aligned} T_{f}=\frac{-0,52 kg \cdot 333 kJ/kg+0,52kg \cdot 4,186 kJ/kg ºC\cdot 70ºC}{0,52kg \cdot 4,186 kJ/kg ºC+0,52kg \cdot 4,186 kJ/kg ºC}=-4,77ºC \end{aligned}\]
Este resultado no es lógico físicamente hablando. Es decir, un
sistema aislado no puede tener una temperatura de equilibrio que fue
menor a la menor de las temperaturas, ni mayor a la mayor de las
temperaturas de las sustancias que componen el sistema. En este caso
particular, la temperatura de equilibrio está por debajo de cero grado.
Como conclusión, no se derrite todo el hielo, teniendo que calcular la
cantidad de hielo que se derrite, y la temperatura de equilibrio será
cero grados.
Entonces, ahora podemos escribir:
\[\begin{aligned} & &\sum Q=0 \nonumber \\ & &Q_{agua}+Q_{\textbf{fusión del hielo}}=0 \nonumber \\ & &m_{agua}\cdot C_{e}\left(T_{f}-T_{i}^{agua}\right)+m_{hielo}\cdot L=0\nonumber \\ & &0,52kg \cdot 4,186 kJ/kg ºC \cdot \left(0ºC-70ºC\right)+m \cdot 333 kJ/kg=0 \end{aligned}\]
Despejando \(m\) de la ecuación anterior, tenemos:
\[\begin{aligned} \label{ej_masa} m&=&\frac{0,52kg \cdot 4,186 kJ/kg ºC \cdot \left(0ºC-70ºC\right)}{333 kJ/kg} \nonumber \\ m&=&0,4576 kg \end{aligned}\]
Como la masa de hielo es de 520 g, entonces nos queda sin
derretir \(m=520g-457,6g=62,4
g\).
Ahora analizaremos el caso en el que el té caliente esté inicialmente a
90ºC. Supondremos inicialmente que se derrite todo el hielo, entonces
usando la ecuación [ej_calor] tenemos:
\[\begin{aligned} T_{f}=\frac{-0,52 kg \cdot 333 kJ/kg+0,52kg \cdot 4,186 kJ/kg ºC\cdot 90ºC}{0,52kg \cdot 4,186 kJ/kg ºC+0,52kg \cdot 4,186 kJ/kg ºC}=5,22ºC \end{aligned}\]
Si hubiésemos planteado el problema suponiendo que la masa de hielo no se derrite completamente, entonces usando la ecuación [ej_masa] para una temperatura inicial del té de 90ºC, tenemos:
\[\begin{aligned} m&=&\frac{0,52kg \cdot 4,186 kJ/kg ºC \cdot \left(0ºC-90ºC\right)}{333 kJ/kg} \nonumber \\ m&=&0,588 kg \end{aligned}\]
Si analizamos un poco este resultado, vemos que es contradictorio al supuesto que no se derrite toda la masa de hielo. Además, la masa de hielo que se derrite es mayor que la inicial (520 g), algo ilógico. Como conclusión, el sistema está en equilibrio a los \(5,22ºC\) y se derrite todo el hielo.
\(\blacksquare\)
Ecuación de Estado - Ley de los Gases Ideales
La ecuación de estado de un sistema da una relación fundamental entre las cantidades termodinámicas macroscópicas. Esta ecuación viene dada por:
\[\begin{aligned}
\label{ec_estado}
pV=nRT
\end{aligned}\] donde \(R=8,3145 \quad
J/mol \cdot K\) y es llamada la contante universal de los gases.
Esta constante es idéntica para todos los gases.
Cuando la cantidad \(n\) es constante,
podemos escribir a la ecuación [ec_estado]
como:
\[\begin{aligned} \label{ec_estado_t} \frac{pV}{T}=\textbf{constante} \end{aligned}\]
Ejemplo 7.3. Un cilindro aislado equipado con un
émbolo, contiene oxígeno a una temperatura de 20ºC y una presión de 15
atm en un volumen de 22 litros. Al descender el émbolo, disminuye el
volumen del gas a 16 litros y simultáneamente la temperatura se eleva a
25ºC. Suponiendo que el oxígeno se comporta como un gas ideal bajo estas
condiciones, ¿cuál es la presión final del gas?
Solución
Partiendo de la ecuación [ec_estado_t], dado que la cantidad de gas permanece sin cambio, tenemos que:
\[\begin{aligned} \frac{p_{i}V_{i}}{T_{i}}&=&\frac{p_{f}V_{f}}{T_{f}} \nonumber \\ p_{f}&=&\frac{p_{i}\cdot V_{i} \cdot T_{f}}{T_{i}\cdot V_{f}} \nonumber \\ p_{f}&=&\frac{15 \textbf{atm} \cdot 22 l \cdot 20ºC}{25ºC \cdot 16 l}=21 \textbf{atm} \end{aligned}\]
\(\blacksquare\)
Trabajo efectuado sobre un gas ideal
Definición 7.4. Gas Ideal
Un gas ideal es un gas teórico compuesto de un conjunto de
partículas puntuales con desplazamiento aleatorio que no interactúan
entre sí. El concepto de gas ideal es útil porque el mismo se comporta
según la ley de los gases ideales.
Un mol de un gas ideal ocupa 22,4 litros a 0ºC de temperatura y 1
atmósfera de presión.
Consideremos, por ejemplo, un gas dentro de un cilindro. Las
moléculas del gas chocan contra las paredes cambiando la dirección de su
velocidad. El efecto del gran número de colisiones que tienen lugar en
la unidad de tiempo, se puede representar por una fuerza \(F\) que actúa sobre toda la superficie de
la pared.
Si una de las paredes es un émbolo móvil de área \(A\) y éste se desplaza una cantidad \(\Delta x\), el intercambio de energía del
sistema con el exterior puede expresarse como el trabajo realizado por
la fuerza \(F\) a lo largo del
desplazamiento \(\Delta x\) (ver
Capítulo 3). Por lo tanto, se puede escribir el
trabajo como:
\[\begin{aligned} W=F \cdot \Delta x \end{aligned}\] teniendo en cuenta que la presión es fuerza por unidad de área, y que el volumen es área por distancia (en nuestro caso \(\Delta x\)), entonces se puede reescribir el trabajo como:
\[\begin{aligned} W=F \cdot \Delta x = - \int p dV \end{aligned}\]
El signo negativo de la fuerza entra porque la fuerza está en
dirección opuesta al desplazamiento.
Trabajo efectuado a volumen constante
El trabajo efectuado es cero en cualquier proceso que el volumen
permanesca constante.
\[\begin{aligned} W=0 \end{aligned}\]
Trabajo efectuado a presión constante
Cuando la presión es constante se puede demostrar que el trabajo
realizado es el siguiente:
\[\begin{aligned} W=-p \left( V_{f} - V_{i} \right) \end{aligned}\]
Trabajo efectuado a temperatura constante
En el caso de que la temperatura sea constante, el trabajo realizado
será:
\[\begin{aligned} W=-nRT \ln{\frac{V_{f}}{V_{i}}} \end{aligned}\]
Capacidad Calorífica de un gas ideal
Introduzcamos cierta energía como calor \(Q\) en un gas que está confinado dentro de
un cilindro equipado con un émbolo. El gas puede entonces (1) almacenar
la energía en forma de energía cinética al azar en sus moléclas, o bien
(2) usar la energía para hacer un trabajo sobre el émbolo.
Capacidad Calorífica a volumen constante
Consideremos primero el caso en el que el émbolo está fijo, de modo que
el volumen del gas permanece constante y no se efectúa ningún trabajo
externo. En este caso, la energía térmica \(Q\) se transforma en energía cinética (o
también llamada energía interna), es decir:
\[\begin{aligned} Q=\Delta E_{int} \end{aligned}\]
Llamemos \(C_{v}\) a la capacidad calorífica a volumen constante, y llamemos \(n\) a la cantidad de moles que contiene el gas, entonces:
\[\begin{aligned} C_{v}=\frac{Q}{n\Delta T}=\frac{\Delta E_{int}}{n\Delta T} \end{aligned}\]
El valor que toma la capacidad calorífica dependerá de la cantidad de átomos que forman la molécula, por lo que se puede demostrar:
| Tipo de átomo | Valor de \(C_{v}\) |
|---|---|
| Monoatómico | \(3/2\cdot R\) |
| Diatómico | \(5/2\cdot R\) |
| Poliatómico | \(3\cdot R\) |
Capacidad Calorífica a presión constante
Cuando mantenemos constante la presión, existen dos tipo de
contribuciones al cambio de energía interna, (1) el calor transferido al
gas, (2) el trabajo \(W\) realizado
sobre el gas. Es decir:
\[\begin{aligned} Q=\Delta E_{int}-W \end{aligned}\]
Acá estamos considerando que el calor transferido desde el entorno es
positivo y tiende a incrementar la energía interna. Si el volumen
disminuye (manteniendo la presión constante), el trabajo efectuado sobre
el gas por el entorno es positivo y tiende a incrementar la energía
interna. Si el volumen aumenta, el gas efectúa un trabajo sobre el
entorno, lo cuál tiende a disminuir la energía interna del gas.
El calor trasnferido en un proceso a presión constante puede escribirse
como:
\[\begin{aligned} Q=n C_{p}\Delta T \end{aligned}\] donde \(C_{p}\) es la capacidad calorífica a presión constante. Puede demostrarse la siguiente igualdad:
\[\begin{aligned} C_{p}=C_{v}+R \end{aligned}\]
| Tipo de átomo | Valor de \(C_{p}\) |
|---|---|
| Monoatómico | \(5/2\cdot R\) |
| Diatómico | \(7/2\cdot R\) |
| Poliatómico | \(4\cdot R\) |
Ejemplo 7.4. Una familia entra en una cabaña de
vacaciones de invierno que no ha sido calentada en un tiempo tan largo
que la temperatura del interior es la misma que la temperatura del
exterior (0ºC). La cabaña cuenta con una sala de 6 m por 4 m en la
superficie y una altura de 3 m. La sala contiene un calefactor eléctrico
de 2 kW. Suponiendo que la sala sea perfectamente hermética y que todo
el calor del calefactor es absorbido por el aire, no escapando nada a
través de las paredes o absorvido por el mobiliario, ¿cuánto tiempo
después de que haya sido encendido el calefactor se alcanzará la
temperatura de 21ºC? Suponer que el aire se comporta como un gas
diatómico ideal.
Solución
Primero calculamos el volumen de la sala:
\[\begin{aligned} V=6m \cdot 4m \cdot 3m=72 m^{3}=72000 l \end{aligned}\]
Sabiendo que un mol de un gas ideal ocupa 22,4 litros a 0ºC y 1 atm, entonces, el número de moles es:
\[\begin{aligned} n=\frac{72000 l}{22,4l}=3214 mol \end{aligned}\]
Dado que estamos considerando que la sala es hermética, entonces el volumen es constante, por lo que la absorción de calor es a volumen constante (recordando que el valor de \(C_{v}=5/2\cdot R=20,8J/mol\cdot K\)), entonces:
\[\begin{aligned} Q&=&n C_{v}\Delta T=3214 mol \cdot 20,8 J/mol\cdot K 21 K \nonumber \\ Q&=&1,4 \times 10^{6} J \end{aligned}\]
Como el calefactor entrega una potencia de 2 kW, entonces:
\[\begin{aligned} P=\frac{Q}{t} \end{aligned}\]
Despejando \(t\),
\[\begin{aligned} t=\frac{Q}{P}=\frac{1,4 \times 10^{6} J}{2000 W}=700 s \end{aligned}\]
\(\blacksquare\)
Ejercicios
En cierta casa con energía solar, se almacena energía del sol en barriles de agua. En un lapso de cinco días nublados de invierno, se necesitaron 5,22 GJ para mantener el interior de la casa a 22ºC. Suponiendo que el agua de los barriles estuiera a 50ºC, ¿qué volumen de agua se necesitó?
Respuesta: 44,5 \(m^{3}\)
Si la masa del cuerpo es de 300 g, y el calor específico del Cobre es de 0.092 cal/g°C. Considerando que el cuerpo en principio se encontraba a 55 °C y luego se estabilizó a 30°C ¿Cuál será la cantidad de calor cedida por el cuerpo?
Respuesta: -690 cal
Se colocan 250g de un material a 165ºC en 500g de agua a 20ºC que se encuentra en un recipiente. La temperatura final a la que llega todo el sistema es de 40ºC. ¿Cuál es el calor específico del material?
Respuesta: 0,32 cal/gºC - Carbón Mineral
Suponga que un cuerpo se encuentra a 120ºF. Calcular la temperatura en grados Celsius y grados Kelvin.
En un recipiente aislado, se agregan 250 g de hielo a 0ºC a 600 g de agua a 18ºC. Calcular la temperatura final del sistema y la cantidad de hielo que queda sin derretirse.
Respuesta: Quedan 135 g y el sistema está a 0ºC
Electricidad
Introducción
Los fenómenos electrostáticos, como escuchar chasquidos al sacarnos
una prenda de vestir, peinar varias veces nuestro cabello seco y luego
acercarlo a pequeños trozos de papel, por ejemplo, se producen por la
interacción de la carga eléctrica de un cuerpo con la de otro. La
palabra electricidad proviene del término élektron, palabra con que los
griegos llamaban al ámbar.
Cuando un átomo, o un cuerpo, tiene la misma cantidad de cargas
positivas (protones) y negativas (electrones) se dice que está
eléctricamente neutro. Si se produce un desequilibrio entre la cantidad
de electrones y protones, se dice que está electrizado. El cuerpo que
pierde electrones queda con carga positiva y el que recibe electrones
queda con carga negativa. Se llama carga eléctrica (\(q\)) al exceso o déficit de electrones que
posee un cuerpo respecto al estado neutro. La carga neta corresponde a
la suma algebraica de todas las cargas que posee un cuerpo.
La carga eléctrica permite cuantificar el estado de electrización de los
cuerpos siendo su unidad mínima la carga del electrón. Esto significa
que la carga eléctrica \(q\) de un
cuerpo está cuantizada y se puede expresar como \(nq\), en que \(n\) es un número entero (incluyendo el
cero); sin embargo, como la carga del electrón es muy pequeña, se
utiliza un múltiplo de ella: el coulomb (\(C\)), que es la carga obtenida al reunir
\(6,24 \times 10^{18}\) electrones.
También se usan con mayor frecuencia los submúltiplos del coulomb: el
microcoulomb (\(\mu C\)) que equivale a
\(10^{-6} C\).
Definición 8.1 (Carga eléctrica). La carga eléctrica es una propiedad física intrínseca de algunas partículas subatómicas que se manifiesta mediante fuerzas de atracción y repulsión entre ellas. La materia cargada eléctricamente es influida por los campos electromagnéticos, siendo a su vez, generadora de ellos. La denominada interacción electromagnética entre carga y campo eléctrico es una de las cuatro interacciones fundamentales de la física. Las cargas del mismo signo se repelen y las de signo contrario se atraen.
Formas para electrizar un cuerpo
Al observar lo que sucede cuando frotamos con nuestra ropa una regla
plástica y la acercamos a las hojas de un cuaderno o al ?hilo? de agua
que cae por una llave de agua, o cuando notamos una chispa al tocar a
una persona luego de caminar por una alfombra en un día de verano, entre
otros ejemplos, podemos inferir que la materia se puede
electrizar.
Un cuerpo eléctricamente neutro se electriza cuando gana o pierde
electrones.
Existen tres formas básicas de modificar la carga neta de un cuerpo:
electrización por frotamiento, contacto e inducción. En todos estos
mecanismos siempre está presente el principio de conservación de la
carga, que nos dice que la carga eléctrica no se crea ni se destruye,
solamente se transfiere de un cuerpo a otro.
Frotamiento. En la electrización por fricción, el cuerpo menos conductor saca electrones de las capas exteriores de los átomos del otro cuerpo quedando cargado negativamente y el que pierde electrones queda cargado positivamente.
Contacto. En la electrización por contacto, el que tiene exceso de electrones (carga -) traspasa carga negativa al otro, o el que tiene carencia de ellos (carga +) atrae electrones del otro cuerpo. Ambos quedan con igual tipo de carga.
Inducción. Al acercar un cuerpo cargado al conductor neutro, las cargas eléctricas se mueven de tal manera que las de signo igual a las del cuerpo cargado se alejan en el conductor y las de signo contrario se aproximan al cuerpo cargado, quedando el conductor polarizado. Si se hace contacto con tierra en uno de los extremos polarizados, el cuerpo adquiere carga del signo opuesto.
Fuerza Eléctrica
Dos cargas eléctricas del mismo signo se repelen, mientras que si son de signos contrarios se atraen. Esta fuerza eléctrica de atracción o repulsión, depende de las cargas eléctricas y de la distancia entre ellas.
Ley de Coulomb
Las primeras experiencias que permitieron cuantificar la fuerza
eléctrica entre dos cargas se deben al francés Charles Coulomb, en el
año 1785. A partir de sus resultados, Coulomb enunció una ley que
describe esta fuerza, de atracción o de repulsión, la que es conocida
como ley de Coulomb, y que es un principio fundamental de la
electrostática.
Los experimentos de Coulomb y de sus contemporáneos demostraron que la
fuerza eléctrica ejercida por un cuerpo cargado sobre otro depende
directamente del producto de sus magnitudes e inversamente del cuadrado
de su separación. En otras palabras,
\[\begin{aligned}
\label{coulomb}
F=K\cdot \frac{ q_{1} q_{2}}{r^{2}}
\end{aligned}\] donde \(K=8.99 \times
10^{9} N m^{2} /C^{2}\). Nosotros nos detendremos en los casos
unidimensionales.
Debemos tener en cuenta que el signo de las cargas nos indicará si la
fuerza es de atracción (cargas con distinto signo) o de repulsión
(cargas con igual signo). El sentido y dirección de la fuerza neta se
infiere a partir del diagrama de fuerzas
Ejemplo 8.1. Suponga que hay tres cargas \(q_{1}=-1,2 \mu C\), \(q_{2}=3,7 \mu C\) y \(q_{3}=-2,3 \mu C\). Si \(q_{2}\) se encuentra a la derecha de \(q_{1}\) a una distancia de \(15 cm\) y un ángulo de cero grado, y \(q_{3}\) a la izquierda de \(q_{1}\) a \(10
cm\) de distancia y un ángulo de 32 grados respecto a la
vertical. Calcular la fuerza eléctrica actuante sobre \(q_{1}\).
 |
Solución
Comencemos calculando la fuerza que ejerce \(q_{2}\) sobre \(q_{1}\), es decir:
\[\begin{aligned} F_{12}&=&\frac{K q_{1} q_{2}}{r_{12}^{2}}=\frac{8,99 \times 10^{9}Nm^{2}/C^{2} \cdot 1,2 \times 10^{-6} C \cdot 3,7 \times 10^{-6} C}{(0,15m)^{2}} \nonumber \\ F_{12}&=&1,77 N \end{aligned}\]
Estas dos cargas tienen signos opuestos, por lo que la fuerza es atractiva. Ahora, calculando la fuerza que ejerce \(q_{3}\) sobre \(q_{1}\), tenemos:
\[\begin{aligned} F_{13}&=&\frac{K q_{1} q_{3}}{r^{2}}=\frac{8,99 \times 10^{9}Nm^{2}/C^{2} \cdot 1,2 \times 10^{-6} C \cdot 2,3 \times 10^{-6} C}{(0,10m)^{2}} \nonumber \\ F_{13}&=&2,48 N \end{aligned}\]
Teniendo en cuenta que las cargas tienen los mismos signos, entonces la fuerza es repulsiva.
Por otra parte, descomponiendo las fuerzas sobre los ejes cartesianos, tenemos:
\[\begin{aligned} F_{1x}&=&F_{12x}+F_{13x}=F_{12}+F_{13}\sen{\theta} \nonumber \\ &=&1,77 N + 2,48 N \sen{32º}=3,08 N \end{aligned}\]
En el eje \(y\) se tiene:
\[\begin{aligned} F_{1y}&=&F_{12y}+F_{13y}=0+F_{13}\cos{\theta} \nonumber \\ &=&0 - 2,48 N \cos{32º}=-2,10 N \end{aligned}\]
Luego, sumando vectorialmente los resultados de ambas componentes, utilizando el teorema de Pitágoras:
\[\begin{aligned} F_{1}=\sqrt{F_{1x}^{2}+F_{1y}^{2}}=\sqrt{(3,08N)^{2}+(-2,10N)^{2}}=3,73 N \end{aligned}\]
Por otro lado, se puede calcular, usando trigonometría, el ángulo de la fuerza \(F_{1}\):
\[\begin{aligned} \tan{\alpha}=\frac{F_{1x}}{F_{1y}}=\frac{3,08 N}{-2,10 N}=-1,466 \end{aligned}\] donde sacando el arcotangente de \(-1,466\) se obtiene un ángulo de \(-56º\).
\(\blacksquare\)
Campo Eléctrico
Las cargas eléctricas generan en torno a ellas, un campo eléctrico de
carácter vectorial que disminuye con la distancia. Este campo produce
una fuerza eléctrica sobre una carga que se ubique en algún punto de
él.
Fue Michael Faraday (1791-1867) quien introdujo la noción de campo en la
Física para poder explicar la interacción a distancia (interactuar sin
tocarse) que ocurre entre cuerpos, como sucede por ejemplo al aproximar
dos imanes, y que Newton no pudo aclarar. En Física, el concepto de
campo señala un sector del espacio en el que a cada punto de él, se le
puede asociar un vector o una cantidad escalar.
Por ejemplo, la Tierra genera un campo gravitatorio en el espacio que la
circunda ejerciendo una fuerza (el peso, que es un vector) sobre los
cuerpos situados en sus cercanías. Del mismo modo, una partícula cargada
Q, llamada carga generadora, produce un campo eléctrico a su alrededor.
Este campo se puede detectar si colocamos una pequeña carga de prueba
\(+q_{0}\) puesta en el punto del
espacio donde se desea medir. En ese punto, la intensidad del campo
eléctrico \(\overline{E}\) es igual a
la fuerza eléctrica que experimenta la carga de prueba y tiene la misma
dirección que la fuerza, si \(q_{0}\)
es positiva; por tanto:
\[\begin{aligned} \label{campo_elec} E=K\frac{Q}{r^{2}} \end{aligned}\]
El campo generado por una carga puntual \(Q\) disminuye con el cuadrado de la
distancia desde la carga. Cualquier campo eléctrico que varíe con la
distancia se denomina campo eléctrico variable y su intensidad solo
depende de la carga generadora y de la distancia entre la carga y el
punto del espacio donde se calcula, independiente de que haya o no una
carga de prueba en ese punto.
Por otra parte, combinando la Ley de Coulomb ([coulomb]) y la
ecuación ([campo_elec]), se puede escribir que el
campo eléctrico es igual a:
\[\begin{aligned} E=\frac{F}{q} \end{aligned}\]
La dirección del campo eléctrico, e incluso su magnitud, puede
representarse mediante las denominadas líneas de fuerza o de
campo.
Las líneas de campo se representan según las siguientes reglas:
Siempre se dibujan desde las cargas positivas (o desde el infinito) hacia las negativas (o hacia el infinito).
La dirección del campo eléctrico en un punto nos la indica la tangente de la línea de campo en ese punto.
El número de líneas es proporcional a la carga.
La densidad de líneas en un punto nos indica la magnitud del campo eléctrico en dicho punto.
Las líneas de campo nunca se cruzan.
A grandes distancias de un sistema de cargas, las líneas son radiales con el mismo espaciado, como si procedieran de una sola carga puntual igual a la carga neta.
Debido a que el campo eléctrico es inversamente proporcional al cuadrado de la distancia a la carga, a medida que nos alejamos de la carga, el campo eléctrico se debilita y las líneas se separan (el espaciado de las líneas de campo está relacionado con la intensidad del campo eléctrico).
 |
 |
Energía potencial eléctrica
Para levantar un objeto desde el suelo hasta cierta altura es
necesario efectuar un trabajo sobre él para vencer la fuerza de gravedad
debida al campo gravitacional terrestre. El objeto en esa posición,
adquiere energía potencial gravitatoria. Si levantamos un cuerpo del
doble de masa, la energía potencial será también el doble, si la masa es
el triple, la energía requerida será también el triple, y así
sucesivamente.
Lo mismo ocurre en el caso de las cargas eléctricas. Si se quiere mover
una carga de prueba \(q\) desde el
infinito (región alejada donde el potencial eléctrico de la carga
generadora es prácticamente nulo) hasta cierto punto dentro de un campo
eléctrico generado por una carga \(Q\),
es necesario ejercer una fuerza por un agente externo, y por tanto
realizar un trabajo contra las fuerzas eléctricas, por lo que la carga
de prueba adquiere una cierta energía potencial eléctrica (\(U\)).
El trabajo \(W\) realizado para mover
la carga de prueba corresponde al cambio de la energía potencial
eléctrica, experimentado por dicha carga. De hecho, si soltamos la carga
\(q\), acelerará alejándose de \(Q\) y transformando la energía potencial
ganada en cinética.
Si definimos que en el infinito \(U =
0\), tenemos que la energía potencial eléctrica que adquiere una
carga puntual \(q\) a una distancia
\(r\) de una carga generadora \(Q\) es:
\[\begin{aligned} U=K\frac{Qq}{r} \end{aligned}\]
Como toda forma de energía, la unidad de la energía potencial eléctrica en el SI es el joule (\(J\)) y será positiva cuando la fuerza sea repulsiva.
Potencial Eléctrico
Si una carga eléctrica \(q\) situada en un punto de un campo eléctrico se duplica, triplica o aumenta n veces, la energía potencial eléctrica aumentará en la misma cantidad, respectivamente; sin embargo, es más frecuente considerar, en dicho punto, el potencial eléctrico (\(V\)), que corresponde a la energía potencial eléctrica por unidad de carga ya que este valor será el mismo, independiente de la cantidad de cargas, o incluso si no hay cargas (es una propiedad del espacio). Por lo tanto:
\[\begin{aligned} V=\frac{U}{q}=K\frac{Q}{r} \end{aligned}\]
El potencial eléctrico es una cantidad escalar, cuya unidad de medida es el volt, en honor del físico italiano Alessandro Volta (creador de la pila eléctrica) que corresponde a \(J/C\). Por ejemplo, un potencial de \(220 V\) significa que en ese punto una carga de \(1 C\) adquiere una energía de \(220 J\).
Ejemplo 8.2. Una placa conductora cargada positivamente crea en sus proximidades un campo eléctrico uniforme \(E = 1000 N/C\), tal y como se muestra en la figura. Desde un punto de la placa se lanza un electrón con velocidad \(10^{7} m/s\) formando un ángulo de 60º con dicha placa, de forma que el electrón describirá una trayectoria como la indicada en la figura. (Datos: \(e = -1,6\times 10^{-19} C\), \(m_{e} = 9,1\times 10^{-31} kg\))
En el punto A, el más alejado de la placa, ¿con qué velocidad se mueve el electrón? Respecto al punto inicial, ¿cuánto ha variado su energía potencial electrostática? Calcula la distancia d entre el punto A y la placa.
Determina la velocidad (módulo y orientación) del electrón cuando choca con la placa (punto B).
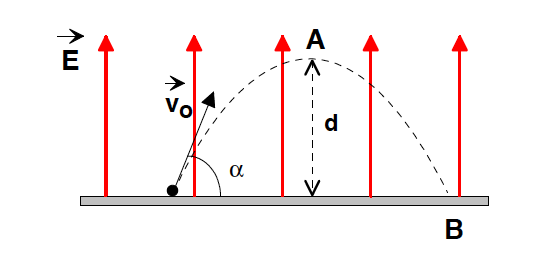 |
Solución
Sobre el electrón está actuando una fuerza, vertical y hacia abajo, de módulo \(F=eE\), siendo \(e\) el valor de la carga del electrón. Usando la segunda ley de Newton, la aceleración, también vertical y hacia abajo, del electrón vale:
\[\begin{aligned} a_{y}=\frac{eE}{m_{e}} \end{aligned}\]
Si se toma como origen de coordenadas la posición inicial del electrón; entonces, la posición del electrón, en cualquier instante, está dada por
\[\begin{aligned} x&=&v_{0x}t=v_{0} \cos{\alpha} \cdot t \\ y&=&v_{0y}t-\frac{1}{2}a_{y}t^{2}=v_{0} \sin{\alpha} \cdot t + \frac{1}{2} \frac{eE}{m_{e}}t^{2} \end{aligned}\]
Esto es debido a que en el eje \(x\) se desarrolla un movimiento del tipo MRU y en el eje \(y\) MRUV, donde sólo actúa la aceleración debida al campo eléctrico \(E\). Las componentes de la velocidad instantánea vienen dadas por:
\[\begin{aligned} v_{x}&=&v_{0x}=v_{0} \cos{\alpha} \\ v_{y}&=&v_{0y}-a_{y}t=v_{0} \sin{\alpha} + \frac{eE}{m_{e}}t \end{aligned}\]
En el punto A, la componente \(y\) de la velocidad (\(v_{y}\)) es nula, por lo tanto
\[\begin{aligned} v_{x}=v_{0x}=v_{0} \cos{\alpha} =5 \times 10^{6} m/s \end{aligned}\]
Para calcular la energía potencial electrostática tenemos que:
\[\begin{aligned} \Delta U=K\frac{Q q}{r}=\Delta V q \end{aligned}\] donde:
\[\begin{aligned} \Delta V=E r \end{aligned}\]
En este caso \(r=d\), por lo que habría que calcular primero la distancia \(d\). Para ello se debe usar la siguiente condición \(v_{y}=0\), es decir:
\[\begin{aligned} v_{y}&=&v_{0} \sin{\alpha} + \frac{eE}{m_{e}}t=0 \end{aligned}\]
De esta ecuación despejamos el tiempo \(t\) y lo reemplazamos en la ecuación \(y\), es decir:
\[\begin{aligned} t&=&\frac{-v_{0} \sin{\alpha}\cdot m_{e}}{e E}=\frac{-10^{7} m/s \cdot \sin{60º}\cdot 9,1\times 10^{-31} kg}{-1,6\times 10^{-19} C \cdot 1000N/C}=4,9 \times 10^{-7} s \nonumber \\ y&=&v_{0} \sin{\alpha} \cdot t + \frac{1}{2} \frac{eE}{m_{e}}t^{2} = 21,3 m \end{aligned}\]
Luego, volviendo a la ecuación de la energía potencial electrostática:
\[\begin{aligned} \Delta U=E\cdot d \cdot e=- 3,4 \times 10^{-15} J \end{aligned}\]
Para calcular la velocidad del electrón cuando llega a la placa, debemos primero calcular el tiempo que tarda el electrón en volver a la placa; por lo que se debe cumplir que \(y=0\), es decir:
\[\begin{aligned} y&=&v_{0} \sin{\alpha}\cdot t + \frac{1}{2} \frac{eE}{m_{e}}t^{2}=0 \end{aligned}\]
Despejando de esta ecuación \(t\), se obtiene:
\[\begin{aligned} t&=&0 \\ t&=&\frac{2 m_{e}v_{0} \sin{\alpha}}{e E}=9,9 \times 10^{-7} s \end{aligned}\]
Las componentes de la velocidad en ese instante son:
\[\begin{aligned} v_{x}&=&v_{0} \cos{\alpha} =5 \times 10^{6} m/s \\ v_{y}&=&v_{0} \sin{\alpha} + \frac{eE}{m_{e}} \cdot t = -8,7 \times 10^{6} m/s \end{aligned}\]
Luego, con las componentes de cada eje se calcula el valor del modulo de la velocidad,
\[\begin{aligned} v=\sqrt{v_{x}^{2}+v_{y}^{2}}=10^{7} m/s \end{aligned}\]
Este valor coincide con el de la velocidad inicial, esto es debido a que la energía mecánica se conserva. Por último, el ángulo de la velocidad viene dado por:
\[\begin{aligned} \beta=\arctan{\frac{v_{y}}{v_{x}}}=-60º \end{aligned}\]
\(\blacksquare\)
Ejemplo 8.3. Un electrón se deja en reposo en el origen de coordenadas donde actúa un campo eléctrico uniforme de intensidad: E = 400 N/C. Determina la diferencia de potencial entre el origen de coordenadas y el punto A(5,0) cm. Calcula la velocidad del electrón cuando pasa por el citado punto A.
 |
Solución
Al realizar un desplazamiento desde el origen de coordenadas hasta el punto A, el vector campo eléctrico y el desplazamiento forman un ángulo de 180º. Aplicando la relación entre el potencial y el campo, se tiene:
\[\begin{aligned} E \cos{\alpha}&=&-\frac{\Delta V}{\Delta r} \nonumber \\ \Delta V&=&400 N/C \cdot \cos{180º} \cdot 0,05 m=20 V \end{aligned}\]
El punto A está a mayor potencial que el punto O, ya que el campo
eléctrico tiene el sentido del potencial decreciente. Si al origen de
coordenadas se le asigna un potencial eléctrico igual a cero voltios, el
punto A está a un potencial de \(20V\).
Para calcular la velocidad del electrón, se hace uso de la ley de la
conservación de la energía mecánica,
\[\begin{aligned} U_{O}+E_{cO}&=&U_{A}+E_{cA} \nonumber \\ 0+0&=&q_{e} V_{A}+\frac{1}{2}m_{e}v_{A}^{2} \nonumber \\ v_{A}&=&\sqrt{\frac{-2q_{e} V_{A}}{m_{e}}}=2,65 \times 10^{6} m/s \end{aligned}\]
\(\blacksquare\)
Ejemplo 8.4. Dos pequeñas bolas, de 10 g de masa cada una de ellas, están suspendidas del mismo punto mediante dos hilos de 1 m de longitud cada uno. Si al cargar las bolitas con la misma carga eléctrica, los hilos se separan formando un ángulo de 10º, determina el valor de la carga eléctrica.
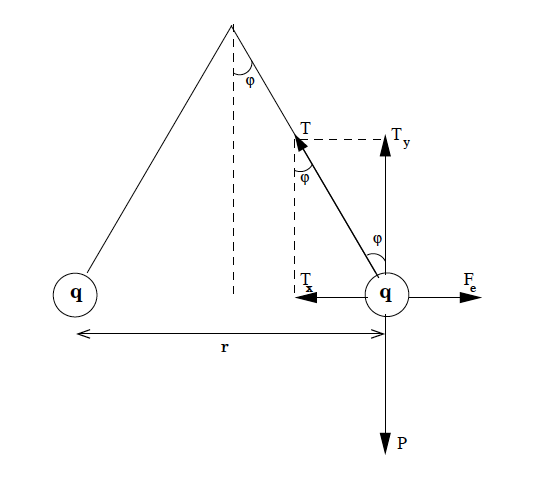 |
Solución
Sobre cada bola actúan su peso, la tensión del hilo y la fuerza eléctrica. Aplicando la condición de equilibrio, se tiene que:
\[\begin{aligned} \sum{F_{x}}&=&0 \Rightarrow T_{x}-F_{e}=0 \Rightarrow T \sin{\varphi}=\frac{Kq^{2}}{r^{2}} \\ \sum{F_{y}}&=&0 \Rightarrow T_{y}-P=0 \Rightarrow T \cos{\varphi}=m g \end{aligned}\]
Dividiendo ambas ecuaciones:
\[\begin{aligned} \tan{\varphi}&=&\frac{Kq^{2}}{m g r^{2}} \Rightarrow q=\sqrt{\frac{m g r^{2} \tan{\varphi}}{K}} \end{aligned}\]
Si la longitud del hilo es igual a d y como cada bola se separa de la vertical un ángulo \(\varphi = 5º\), la distancia entre ellas es: \(r = 2 d \cdot sin 5º\). Sustituyendo en la ecuación anterior:
\[\begin{aligned} q=\sqrt{\frac{m g (2 d \cdot sin 5º)^{2} \tan{\varphi}}{K}}=1,7 \times 10^{-7} C \end{aligned}\]
\(\blacksquare\)
Ejercicios
Dos cargas puntuales de \(5\mu C\) y \(-2\mu C\) se encuentran separadas a una distancia de 15 cm. Haz un diagrama vectorial de fuerzas y calcula el módulo de la fuerza indicando si la fuerza es atractiva o repulsiva.
Dos cargas puntuales se separan a una distancia tres veces mayor que la que tenían inicialmente. ¿Cómo cambia el módulo de la fuerza eléctrica entre ellas? Explica.
Determina el punto entre dos cargas puntuales de \(+2 mC\) y \(+5 mC\) en que el campo eléctrico es nulo. Ambas cargas se encuentran a 1 m de distancia.
¿Cuál debe ser la distancia entre dos cargas puntuales de \(q_{1}=26,3 \mu C\) y otra de \(q_{2}=-47,1 \mu C\) para que la fuerza eléctrica sea de \(5,66 N\)?
Una carga puntual de \(3,12 \times 10^{-6} C\) se encuentra a una distancia de \(12,3 cm\) de una segunda carga puntual de \(-1,48 \times 10^{-6} C\). Calcular la magnitud de la fuerza entre las cargas.
Determinar la intensidad de la fuerza eléctrica que actúa sobre \(q_{1}\), suponiendo que \(q_{1}=q_{2}=21,3 \mu C\) y \(d=1,52 m\). Ahora suponga que se introduce una tercera carga \(q_{3}=21,3 \mu C\) y se coloca a una distancia de \(1,52 m\) de \(q_{1}\) y \(q_{2}\) formando un triángulo equilátero. Calcular la nueva fuerza que se ejerce sobre \(q_{1}\).
Suponga que hay cuatro cargas que se distribuyen en los vértices de un cuadrado de \(15,2 cm\) de lado. Los vértices del lado izquierdo tienen una carga \(+q\) y \(+2q\), y los vértices del lado derecho \(-q\) y \(-2q\), empezando por arriba en ambos casos. Suponiendo que \(q=1,13 \mu C\), calcular la fuerza eléctrica resultante que opera sobre el ángulo inferior izquierdo.
La masa de un protón es \(1,67 \times 10^{-27} kg\) y su carga eléctrica \(1,6 \times 10^{-19} C\). Compara la fuerza de repulsión eléctrica entre dos protones situados en el vacío con la fuerza de atracción gravitatoria que actúa entre ellos.
Un electrón que lleva una velocidad de \(5 \times 10^{6} m/s\) accede perpendicularmente a un campo eléctrico uniforme de intensidad E = 3000 N/C. Deduce la ecuación de la trayectoria que describe el electrón. ¿Qué distancia recorre verticalmente el electrón después de trasladarse horizontalmente 12 cm?
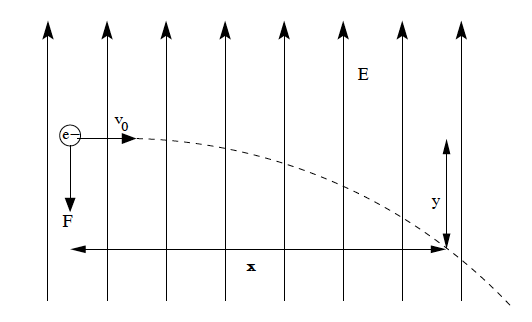
Una partícula cargada negativamente, con masa \(m=8 \times 10^{-20} kg\) y carga \(q=-2\times 10^{-18} C\), describe órbitas circulares alrededor de otra partícula mucho mayor, de masa \(M=4 \times 10^{-12} kg\) y carga positiva \(Q=3\times 10^{-10} C\), a la que supondremos inmóvil. La partícula pequeña emplea un tiempo \(t = 7,65\times 10^{-10} s\) en dar una vuelta completa. No tendremos en cuenta la atracción gravitatoria entre ambas partículas.
Calcula el radio de la órbita que describe la partícula pequeña.
Al no haber tenido en cuenta la fuerza gravitatoria, se puede pensar que estamos cometiendo cierto error. ¿Piensas que dicho error es despreciable? Razona numéricamente tu respuesta.
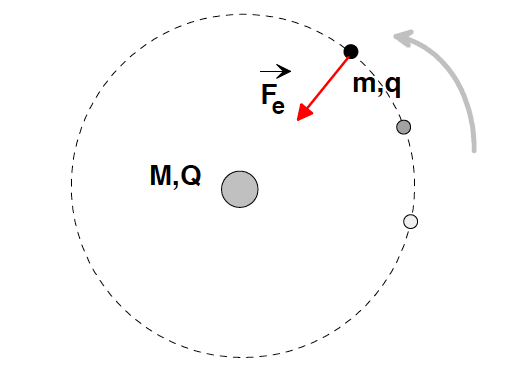
Magnetismo
Introducción
El magnetismo es un fenómeno físico por el que los objetos ejercen
fuerzas de atracción o repulsión sobre otros materiales. Hay materiales
que presentan propiedades magnéticas detectables fácilmente, como el
níquel, el hierro o el cobalto, que pueden llegar a convertirse en un
imán.
Cada electrón es, por su naturaleza, un pequeño imán. Ordinariamente,
innumerables electrones de un material están orientados aleatoriamente
en diferentes direcciones, pero en un imán casi todos los electrones
tienden a orientarse en la misma dirección, creando una fuerza magnética
grande o pequeña dependiendo del número de electrones que estén
orientados.
Además del campo magnético intrínseco del electrón, algunas veces hay
que contar también con el campo magnético debido al movimiento orbital
del electrón alrededor del núcleo. Este efecto es análogo al campo
generado por una corriente eléctrica que circula por una bobina. De
nuevo, en general el movimiento de los electrones no da lugar a un campo
magnético en el material, pero en ciertas condiciones los movimientos
pueden alinearse y producir un campo magnético total medible.
Fuerza Magnética
Toda carga que se mueve en un campo magnético de inducción sufre la acción de una fuerza cuyo módulo viene dado por la expresión:
\[\begin{aligned}
\overrightarrow{F}=q \cdot \overrightarrow{v} \times \overrightarrow{B}
\end{aligned}\] o bien: \[\begin{aligned}
F=q \cdot v \cdot B \sin{\phi}
\end{aligned}\] donde \(q\) es
la carga que se mueve en el campo magnético de inducción (\(B\)) con una velocidad que forma un ángulo
\(\phi\) con el vector inducción
magnética. La dirección viene dada por la regla de la mano derecha (9.2).
Sobre ella actúa una fuerza.
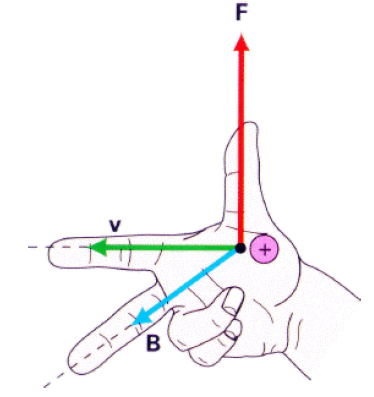 |
Como se puede observar esa fuerza existe si la partícula en movimiento:
Está en el seno de un campo magnético (vector inducción magnética) \(B\)
Tiene carga \(q \neq 0\), sea positiva o negativa.
Está en movimiento y su velocidad no tiene la misma dirección que el vector inducción magnética.
Por otra parte la fuerza que se ejerce sobre esa carga en movimiento:
Es proporcional a la carga.
Es perpendicular a la velocidad y al vector inducción magnética.
Su módulo depende además del ángulo que forman el vector inducción magnética y el vector velocidad.
Ley de Lorentz
Según se ve en el tema de electricidad, la fuerza eléctrica sobre una carga puntual en reposo viene dada por:
\[\begin{aligned} \overrightarrow{F}=q\cdot \overrightarrow{E} \end{aligned}\]
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza es la que llamamos fuerza magnética. Por lo tanto, la fuerza total sobre una carga puntual en movimiento es entonces:
\[\begin{aligned} \overrightarrow{F}=q\cdot (\overrightarrow{E}+\overrightarrow{v} \times \overrightarrow{B}) \end{aligned}\]
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
Campo Magnético
Se trata de un campo que ejerce fuerzas (denominadas magnéticas)
sobre los materiales. Al igual que el campo eléctrico también es un
campo vectorial, pero que no produce ningún efecto sobre cargas en
reposo (como sí lo hace el campo eléctrico en dónde las acelera a través
de la fuerza eléctrica). Sin embargo el campo magnético tiene influencia
sobre cargas eléctricas en movimiento.
Si una carga en movimiento atraviesa un campo magnético, la misma sufre
la acción de una fuerza (denominada fuerza magnética). Esta fuerza no
modifica el módulo de la velocidad pero sí la trayectoria. Sobre un
conductor por el cual circula electricidad y que se encuentra en un
campo también aparece una fuerza magnética.
El campo magnético está presente en los imanes; pero por otro lado, una
corriente eléctrica también genera un campo magnético. El campo
magnético se denomina con la letra \(B\) y se mide en Tesla
(\((N \cdot s)/(C \cdot m)\).
La fuerza magnética y el campo magnético son consecuencia de la
existencia de los polos magnéticos (polos Norte y Sur).
Al igual que en el campo eléctrico, existen lo que se llaman las líneas
de campo magnético, que permiten estimar en forma aproximada el campo
magnético existente en un punto dado, tomando en cuenta las siguientes
características:
Las líneas de campo magnéticos son siempre lazos cerrados que van de norte a sur por fuera del imán y de sur a norte por dentro del imán
Las líneas magnéticos nunca se entrecruzan .
Las líneas magnéticas de imanes diferentes se atraen y se repelen entre sí: las líneas del mismo sentido se atraen y las de sentido opuesto se repelen
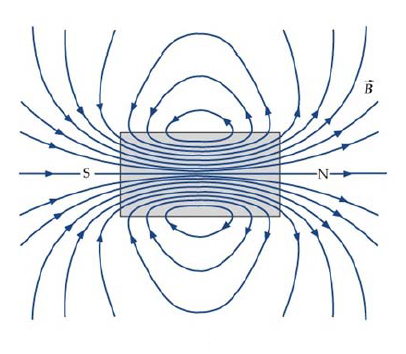 |
Propiedades de los polos magnéticos.
Algunas propiedades son semejantes a las de las cargas eléctricas.
Así:
Polos de distinto signo se atraen entre sí, y polos del mismo signo se repelen.
La fuerza con que los polos interaccionan es inversamente proporcional al cuadrado de la distancia que los separa.
Sin embargo, existe una diferencia fundamental y es que, mientras que una carga eléctrica positiva o negativa puede ser aislada, no pueden aislarse monopolos magnéticos. Al dividir un imán por la mitad, cada una de las dos mitades se convierte en un nuevo imán, con sus polos norte y sur correspondientes.
El campo magnético terrestre
La Tierra posee un poderoso campo magnético, como si el planeta
tuviera un enorme imán en su interior cuyo polo sur estuviera cerca del
polo norte geográfico y viceversa. Aunque los polos magnéticos
terrestres reciben el nombre de polo norte magnético (próximo al polo
norte geográfico) y polo sur magnético (próximo al polo sur geográfico),
su magnetismo real es el opuesto al que indican sus nombres.
Las posiciones de los polos magnéticos no son constantes y muestran
notables cambios de año en año. Cada 960 años, las variaciones en el
campo magnético de la Tierra incluyen el cambio en la dirección del
campo provocado por el desplazamiento de los polos. El campo magnético
de la Tierra tiene tendencia a trasladarse hacia el Oeste a razón de 19
a 24 km por año.
 |
Flujo Magnético
El recorrido de las líneas de fuerza recibe el nombre de circuito magnético, y el número de líneas de fuerza existentes en un circuito magnético se le conoce como flujo magnético. Estas líneas nos dan una idea de:
Dirección que tendrá el campo magnético. Las líneas de campo van desde el polo sur al polo norte en el interior del imán y desde el polo norte hasta el polo sur por el exterior.
La intensidad del campo magnético, es inversamente proporcional al espacio entre las líneas (a menos espacio más intensidad).
En un campo magnético uniforme, la densidad de flujo de campo magnético que atraviesa una superficie plana y perpendicular a las líneas de fuerza valdrá:
\[\begin{aligned}
B=\frac{\Phi}{S}
\end{aligned}\] donde la letra griega \(\Phi\) es el flujo magnético y su unidad es
el Weber (\(Wb=T/m^{2}\)).
En el caso de que la superficie atravesada por el flujo magnético no sea
perpendicular a la dirección de este tendremos que:
\[\begin{aligned} \Phi=B \cdot S \cos{\alpha} \end{aligned}\] donde \(\alpha\) es el ángulo que forma la superficie que atraviesa el flujo y el campo magnético.
Diferencias entre el campo eléctrico y magnético
Podemos mencionar algunas diferencias entre los campos magnéticos y eléctricos y resumirlas en:
La fuerza eléctrica siempre está en la dirección del campo eléctrico, mientras que la fuerza magnética es perpendicular al campo magnético.
La fuerza eléctrica actúa sobre una partícula cargada independientemente de la velocidad de la partícula, mientras que la fuerza magnética actúa solo cuando la partícula cargada se encuentra en movimiento.
La fuerza eléctrica realiza trabajo al desplazar una partícula cargada, mientras que la fuerza magnética asociada a un campo magnético estacionario no realiza trabajo cuando una partícula se desplaza.
Cuando una carga se mueve con una velocidad \(v\), el campo magnético aplicado solo puede alterar la dirección del vector velocidad, pero no puede cambiar la rapidez de la partícula.
Las lineas del campo magnético son cerradas, mientras que lineas del campo eléctrico son abiertas.
Partículas que inciden perpendicularmente al campo magnético
Sobre la partícula aparece una fuerza de valor constante y que es
perpendicular a la velocidad y al campo magnético. Al ser perpendicular
a la velocidad, se constituye una fuerza centrípeta que originará una
variación en la dirección de la velocidad pero no de su módulo. Por lo
tanto, la partícula describirá una movimiento circular uniforme.
Las cargas positivas giran en un sentido y las negativas en el sentido
contrario. El radio de la trayectoria circular que experimentan surge de
igualar la segunda Ley de Newton y la fuerza magnética, es decir:
\[\begin{aligned} F&=& m\cdot a \nonumber \\ F&=& q \cdot B \cdot v \sin{\phi} \nonumber \end{aligned}\]
Sabiendo que \(\phi=90º\), y que la aceleración es igual a la aceleración centrípeta del movimiento circular uniforme, entonces::
\[\begin{aligned} \label{ec_ej_mag1} m\cdot \frac{v^{2}}{R} &=& q \cdot B \cdot v \nonumber \\ R&=&\frac{m\cdot v}{q \cdot B} \end{aligned}\]
Ejemplo 9.1. Un electrón, de energía cinética \(25 kev\) (\(1eV=1,6\times 10^{-19} J\)), se mueve en una órbita circular en el interior de un campo magnético, de \(0,2 T\). Calcular:
La velocidad del electrón
El radio de la órbita
El periodo del movimiento
Datos: \(m_{e} = 9,1\times 10^{-31}
kg\) , \(e = 1,6\times 10^{-19}
C\)
Solución
Teniendo en cuenta que la energía cinética es la única energía presente, y recordando que se define como:
\[\begin{aligned} E_{c}&=&\frac{1}{2}m v^{2} \nonumber \end{aligned}\]
Entonces, despejando la velocidad, tenemos:
\[\begin{aligned} v&=&\sqrt{\frac{2E_{c}}{m}} \nonumber \\ v&=&\sqrt{\frac{2\cdot 25000 \cdot 1,6\times 10^{-19} J}{9,1\times 10^{-31} kg}} \nonumber \\ v&=&9,37\times 10^{7} m/s \end{aligned}\]
Para calcular el radio de la órbita, tenemos que igualar la segunda Ley de Newton y la fuerza magnética, por lo que tenemos:
\[\begin{aligned} F&=& m\cdot a \nonumber \\ F&=& q \cdot B \cdot v \sin{\phi} \nonumber \end{aligned}\]
Teniendo en cuenta que \(\phi=90º\), y que la aceleración es igual a la aceleración centrípeta (\(v^{2}/R\)) del movimiento circular uniforme, entonces se puede escribir:
\[\begin{aligned} \label{ec_ej_mag2} m\cdot \frac{v^{2}}{R} &=& q \cdot B \cdot v \end{aligned}\]
Entonces, despejando \(R\), tenemos:
\[\begin{aligned} R&=&\frac{m\cdot v}{q \cdot B} \nonumber \\ R&=&\frac{9,1\times 10^{-31} kg \cdot 9,37\times 10^{7} m/s}{1,6\times 10^{-19} C \cdot 0,2 T} \nonumber \\ R&=&2,66 \times 10^{-3}m \end{aligned}\]
Para calcular el período partimos de la ecuación ([ec_ej_mag1]), y teniendo en cuenta que la velocidad en el movimiento circular puede ser escrita como:
\[\begin{aligned} v=\frac{2\pi R}{T} \end{aligned}\] y reemplazando en la ecuación ([ec_ej_mag1]) para luego despejar \(T\), tenemos:
\[\begin{aligned} T&=&\frac{2\pi m}{q B} \nonumber \\ T&=&\frac{2\pi 9,1\times 10^{-31} kg}{1,6\times 10^{-19} C \cdot 0,2 T} \nonumber \\ T&=&1,78 \times 10^{-10} s \end{aligned}\]
\(\blacksquare\)
Ejercicios
Una partícula de masa \(m\), carga positiva \(q\) y dotada de velocidad horizontal, penetra en una \(v_{0}\) región del espacio donde hay un campo eléctrico y \(E\) un campo magnético \(B\). Ambos campos son mutuamente perpendiculares y a su vez perpendiculares a la velocidad de la partícula. El campo magnético es perpendicular al papel, dirigido hacia adentro y representado en la figura por ?x?, mientras que el campo eléctrico es paralelo al papel y representado por líneas rectas. Observamos que la partícula no experimenta ninguna desviación. Sin considerar efectos gravitatorios, calcula la expresión de la velocidad de la partícula.
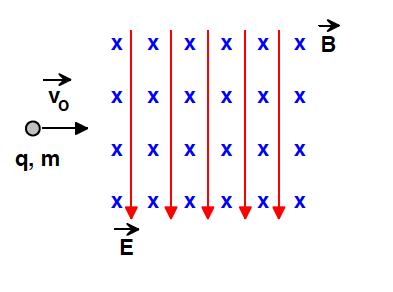
Dos isótopos de un elemento químico, cargados con una sola carga positiva y con masas de \(19,91 \times 10^{-27} kg\) y \(21,59\times 10^{?27} kg\), respectivamente, se aceleran hasta una velocidad de 6,7 · 105 m/s. Seguidamente, entran en una región en la que existe un campo magnético uniforme de 0,85 T y perpendicular a la velocidad de los iones. Determina la relación entre los radios de las trayectorias que describen las partículas y la separación de los puntos de incidencia de los isótopos cuando han recorrido una semicircunferencia.
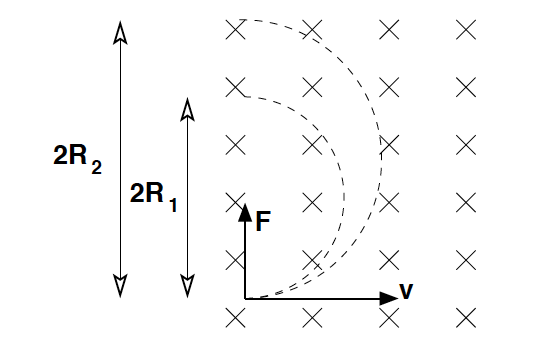
Respuestas: \(R_{1}/R_{2}=0,922\); Separación\(=0,0166 m\)
Un chorro de iones es acelerado por una diferencia de potencial de \(10000 V\), antes de penetrar en un campo magnético de \(1 T\). Si los iones describen una trayectoria circular de \(5 cm\) de radio, determina su relación carga-masa.
Respuestas: \(q/m=8 \times 10^{6} C/kg\)
Una partícula de carga q=- C y masa m= Kg entra con una velocidad \(V=V_{i}\) en una región del espacio en la que existe un campo magnético uniforme \(B=-0,5 T\). El radio de la trayectoria circular que describe es \(R=0,3m\).
Dibujar la fuerza que ejerce el campo sobre la partícula en el instante inicial y la trayectoria que sigue esta. Calcular la velocidad V con la que entro a partir de la segunda ley de Newton en el eje normal.
Calcular el periodo del movimiento y la frecuencia angular ¿Cómo varían el radio de la trayectoria y el periodo del movimiento si se duplica la velocidad de entrada?
Respuestas: \(V=1,4\times 10^{7} m/s\) y \(T=1,34\times 10^{-7}s\)
Un electrón se acelera por la acción de una diferencia de potencial de \(100 V\) y, posteriormente, penetra en una región en la que existe un campo magnético uniforme de \(2 T\), perpendicular a la trayectoria del electrón. Calcula la velocidad del electrón a la entrada del campo magnético. Halla el radio de la trayectoria que recorre el electrón en el interior del campo magnético y el periodo del movimiento.
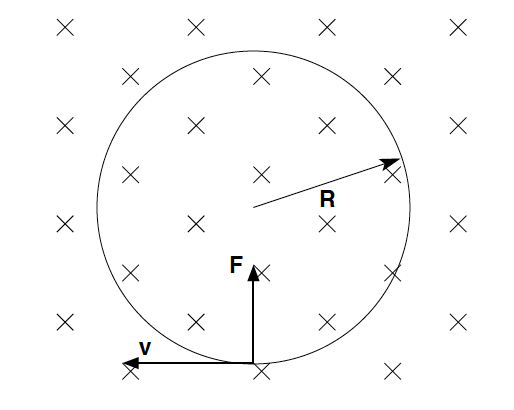
Respuestas: \(V=6\times 10^{6} m/s\); \(R=1,8\times 10^{-5}m\) y \(T=1,8\times 10^{-11}s\)
Un protón tras ser acelerado por una diferencia de potencial de \(25000 V\), penetra perpendicularmente en un campo magnético y describe una trayectoria circular de \(40 cm\) de radio. Determinar:
La inducción magnética.
el radio de la trayectoria para un valor doble de la inducción magnética.
Datos: \(e = +1,6\times 10^{-19} C\) , \(m_{p} = 1,67\times 10^{-27} kg\)
Respuestas: \(B=5688,43T\) y \(R=0,2 m\)En un campo magnético uniforme de valor \(12 T\), que penetra perpendicularmente al plano del papel, entra un electrón con velocidad \(v_{0}= 4\times 10^{6} m/s\) perpendicular a \(B\). Calcular:
La aceleración que adquiere el electrón.
El radio de la trayectoria que describe.
Respuestas: \(a=8,43 \times 10^{18} m/s^{2}\) y \(R=1,89\times 10^{-6} m\)
Astronomía
Historio del Calendario
El primer año de la era romana, denominado el Año de Rómulo,
consistía en diez o doce meses, según la bibliografía que se cite. El
principio del año romano no era enero, como es en la actualidad; era en
marzo, y llegaba hasta diciembre.
Más tarde, se instauró el año de Numa, con doce meses y 355 días. Este
año fue creado alrededor del 700 a. C. Aún de esta manera el año quedaba
corto once días respecto al año solar (estacionario), por lo que Numa
Pompilio ordenó que se le añadiera un mes cada dos años de 22 días en el
segundo y sexto años, y de 23 días en el cuatro y octavo, haciendo un
ciclo de ocho años.
En 45 a. C. Julio César encargó al astrónomo alejandrino Sosígenes la
elaboración de su calendario. Este fijó la duración del año en 365 días
y seis horas, cálculo asombrosamente exacto dados los rudimentarios
instrumentos de la época, ya que su margen de error fue sólo de 11
minutos y 9 segundos al año, es decir, menos de un segundo por día, pero
con el fin de evitar complicaciones, se tomó de 365 días de duración,
añadiendo diez días al año de 355 días.
Julio César añadió un día a julio, mes de su nacimiento. Augusto hizo lo
mismo con agosto. Ambos días fueron retirados de febrero, que pasó a
tener 28. Ante la disminución de este mes con respecto a los otros, el
día añadido de los años bisiestos se le concedió a él.
Julio César estableció que el año comenzara el 1 de enero, día en el que
los funcionarios del emperador asumían su cargo La imperfección del
Calendario Juliano dio pie para que en el año 1582 el Papa Gregorio XIII
encargara a Luis Lilio y al jesuita alemán Christopher Clavius la
reforma por la cual se creó el Calendario Gregoriano.
Esta reforma tuvo dos aspectos principales. Por una parte, dado que el
equinoccio de primavera se había adelantado 10 días, se suprimieron
estos para ajustar el ciclo de las estaciones. Este ajuste se llevó a
cabo el jueves 4 de octubre de 1582, por lo que el siguiente día se
consideró viernes 15 de octubre. Además para conseguir que este
resultado pudiera mantenerse en el futuro, se acordó que los años
bisiestos cuyas dos últimas cifras fueran ceros no serían bisiestos,
excepto si sus dos primeras son divisibles por cuatro. Así pues de los
años 1600, 1700, 1800, 1900 y 2000, que en el calendario juliano son
bisiestos, en el gregoriano lo son sólo el 1600 y el 2000, de modo que
cada cuatro siglos quedan suprimidos tres días.
Leyes de Kepler
Las leyes de Kepler fueron enunciadas por Johannes Kepler para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol. Las tres leyes pueden ser enunciadas de la siguiente manera:
Los planetas giran en órbitas elípticas, ocupando el Sol uno de los focos de la elipse.
Los vectores de posición de los planetas barren áreas iguales en tiempos iguales. La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). Matemáticamente:
\[\begin{aligned} r_{1}\cdot v_{1}=r_{2}\cdot v_{2} \end{aligned}\] donde \(r\) es la distancia al Sol y \(v\) es la velocidad del cuerpo.
Los cuadrados de los periodos orbitales de los planetas son proporcionales al cubo de los semiejes mayores de sus órbitas.
\[\begin{aligned} \frac{T_{1}^{2}}{a_{1}^{3}}=\frac{T_{2}^{2}}{a_{2}^{3}} \end{aligned}\] donde \(T\) son los períodos orbitales y \(a\) es el valor del semieje mayor de la órbita.
Los elementos que comprenden una elipse son los siguientes:
Focos
Eje mayor (semieje mayor)
Eje menor (semieje menor)
Perihelio: punto de la elipse que se encuentra sobre el eje mayor y que se encuentra a la menor distancia del foco que ocupa el cuerpo (Sol).
Afelio: punto de la elipse que se encuentra sobre el eje mayor y que se encuentra a la mayor distancia del foco que ocupa el cuerpo (Sol).
 |
Dado que el eje de rotación de la Tierra se encuentra inclinado respecto al eje de la órbita alrededor del Sol (23,47º aproximadamente), hace que los rayos solares tengan distinto ángulo de incidencia sobre la superficie de la Tierra, provocando las diferentes estaciones del año. En el siguiente gráfico se presenta un esquema que explica éste fenómeno.
 |
Ley de Gravitación Universal
Para empezar, vamos a suponer que las masas son puntuales, es decir que están concentradas en un solo punto y que no tienen volumen alguno (punto material).
La leyenda dice que Newton descubrió el principio de gravitación
universal reflexionando después de ver caer una manzana. La realidad es
que Newton estudió concienzudamente los trabajos de Galileo sobre la
caída de los cuerpos y de Copérnico y Kepler sobre el movimiento
planetario antes de extraer sus propias conclusiones.
Copérnico había establecido el modelo heliocéntrico que Galileo había
demostrado. Los planetas giran alrededor del Sol en órbitas elípticas,
muchas veces casi circulares.
Para que este movimiento se produzca hace falta una fuerza
centrípeta:
\[\begin{aligned} F=m\cdot a \end{aligned}\]
Pero la aceleración centrípeta se puede escribir como:
\[\begin{aligned} a_{c}=\frac{v^{2}}{R} \end{aligned}\]
Entonces:
\[\begin{aligned}
F=\frac{m\cdot v^{2}}{R}
\end{aligned}\] donde \(m\) es
la masa del objeto, \(v\) es su
velocidad y \(R\) el radio de la
trayectoria.
De las leyes de Kepler, Newton dedujo las condiciones matemáticas que
debía cumplir la fuerza gravitatoria. La tercera ley establecía una
relación concreta entre los periodos y los semiejes mayores de las
órbitas que la fuerza gravitatoria debía cumplir.
Finalmente, la Ley de Gravitación de Newton es:
\[\begin{aligned} F=G\frac{m \cdot M}{R^{2}} \end{aligned}\] donde \(G=6,67 \times 10^{-11} N m^{2} kg^{-2}\) es la constante de gravitación universal
Variación de la intensidad de la gravedad
Sabemos que el peso de un cuerpo es \(P=mg\) donde \(m\) es la masa del cuerpo y \(g\) es la intensidad de la gravedad, es decir la fuerza con que la Tierra atrae a un kilogramo de masa. En caída libre en el vacío esta intensidad es idéntica a la aceleración del movimiento. Para Galileo, que estudiaba caídas a pequeñas alturas, \(g\) es una constante Si en la expresión de la fuerza que un cuerpo de masa \(M\) ejerce sobre otro de masa \(m\), calculamos la fuerza por unidad de masa, obtenemos:
\[\begin{aligned} g=\frac{F}{m}=\frac{G\frac{M\cdot m}{R^{2}}}{m}=G\frac{M}{R^{2}} \end{aligned}\]
Donde vemos que \(g\) ya no es una constante, sino que depende de la distancia al centro del planeta.
La masa de los planetas
Las nuevas leyes en la Física no sólo explican hechos observados sino
que muchas veces pueden aplicarse para obtener nuevos conocimientos no
previstos al principio.
El principio de gravitación, por ejemplo, nos permite calcular la masa
de un astro si sabemos los efectos que produce sobre otro.
Por ejemplo, podemos calcular la masa de un planeta sabiendo la
intensidad de la gravedad en la superficie y su radio.
\[\begin{aligned} F=\frac{m\cdot v^{2}}{R}=G\frac{M\cdot m}{R^{2}} \end{aligned}\]
Suponiendo que la órbita de los planetas es circular, entonces la velocidad \(v=2\pi R /T\), entonces se puede escribir:
\[\begin{aligned} M=\frac{4\pi^{2} R^{3}}{G T^{2}} \end{aligned}\]
Movimiento de los satélites
Cuando lanzamos al cielo un satélite artificial, su comportamiento en órbita es similar al de los planetas respecto al Sol. Partiendo de la siguiente ecuación:
\[\begin{aligned} \frac{m\cdot v^{2}}{R}=G\frac{M\cdot m}{R^{2}} \end{aligned}\] y luego simplificando y despejando \(v\) tenemos
\[\begin{aligned} v_{orbital}=\sqrt{G\frac{M}{R}} \end{aligned}\]
Esta velocidad es llamada la velocidad orbital. Por otra parte, se puede demostrar que para que un satélite escape de su órbita la velocidad orbital debe ser igual o superior a la siguiente velocidad:
\[\begin{aligned} v_{escape}=\sqrt{2G\frac{M}{R}} \end{aligned}\]
Distancias en Astronomía
Vamos a empezar definiendo el concepto de paralaje. La distancia
entre nuestro Sol y las estrellas se determina por medio de un efecto
que se denomina paralaje. Supongamos que en una época del año, por
ejemplo en diciembre, observamos una estrella cercana. Respecto de las
estrellas lejanas, que podemos considerar como fijas, vamos a observar
la posición de esa estrella, proyectada en la dirección A. Seis meses
después, en junio, al encontrarse la Tierra en el otro extremo, si se
observa la misma estrella la vamos a ver proyectada sobre el fondo de
estrellas, en la posición B. en esta configuración tenemos un triángulo
rectángulo, con vértices en el Sol, La Tierra y la estrella. El ángulo
se denomina paralaje.
 |
Hay distintas unidades de medida que se usan en astronomía. Estas dependen fundamentalmente de la distancia a la cuál se encuentran los astros en el universo. Vamos a mencionar algunas de las principales unidades:
Unidad Astronómica: equivale a la distancia entre el Sol y la Tierra, unos 150 millones de km. Es muy usada en el Sistema Solar, o para distancias algo mayores al Sistema Solar.
Año Luz: 10 billones de kilómetros. El año-luz es equivalente a la distancia recorrida por la luz en un año a 300 mil km./s o sea 86400 s (día) x 365 x 300.000 km/seg. = casi 10 billones km.
Parsec: 3,26 a.l. (3,26 años luz, algo más de 32 billones de kilómetros). Equivale a la distancia de un objeto que tiene una paralaje de 1 segundo de arco.
Magnitudes
Cuando miramos al cielo en una noche clara vemos estrellas. Vistas
desde la Tierra, unas parecen brillantes y otras muy débiles. Algunas de
estas estrellas débiles son intrínsecamente muy brillantes, pero están
muy lejos. Algunas de las estrellas más brillantes del cielo son
estrellas muy débiles que simplemente se encuentran muy próximas a
nosotros. Cuando observamos, estamos forzamos a hacerlo desde la Tierra
o en sus proximidades, y podemos sólo medir la intensidad de la luz que
nos llega.
Desafortunadamente esto no nos dice de manera directa nada acerca de las
propiedades internas de una estrella. Si queremos saber más acerca de la
estrella, su tamaño o su brillo interno/ físico, por ejemplo,
necesitamos conocer su distancia a la Tierra.
Históricamente, las estrellas visibles a simple vista fueron ordenadas
en seis clases diferentes de brillo, llamadas magnitudes. Este sistema
fue originariamente concebido por el astrónomo griego Hiparco en torno
al año 120 AC y está aún en uso hoy en día en una forma ligeramente
revisada. Hiparco decidió que las estrellas más brillantes tendrían
magnitud 1, y las más débiles magnitud 6.
Sin embargo, incluso los astrónomos de hoy en día usan aún una forma
ligeramente revisada del sistema de magnitudes de Hiparco llamado de
magnitudes aparentes. La definición moderna de magnitud fue elegida de
manera que las medidas de las magnitudes ya en uso no tuvieran que ser
cambiadas. Los astrónomos usan dos tipos diferentes de magnitudes:
magnitudes aparentes y magnitudes absolutas.
Magnitud Aparente
La magnitud aparente, \(m\), de una
estrella mide el brillo de una estrella observado desde la Tierra o
cerca de ella. En lugar de definir la magnitud aparente a partir del
número de fotones de luz que observamos, se define respecto a la
magnitud e intensidad de una estrella de referencia. Esto significa que
un astrónomo puede medir las magnitudes de las estrellas comparando las
medidas con ciertas estrellas estándar que ya han sido medidas de forma
absoluta (en contraposición a las medidas relativas).
La magnitud aparente, \(m\), viene dada
por:
\[\begin{aligned}
m = m_{ref} - 2,5\log_{10} (I/I_{ref})
\end{aligned}\] donde \(m_{ref}\) es la magnitud aparente de la
estrella de referencia, \(I\) es la
intensidad medida procedente de la estrella y \(I_{ref}\) es la intensidad de la luz
procedente de la estrella de referencia. El factor de escala 2,5 nos
equipara la definición moderna con las magnitudes aparentes más antiguas
y más subjetivas.
Para comparar, la magnitud aparente de la Luna llena es aproximadamente
-12,7, la magnitud de Venus puede ser tan alta como -4 y el Sol tiene
una magnitud de aproximadamente -26,5.
Magnitud Absoluta
Ahora tenemos una definición apropiada para la magnitud aparente. Es
una herramienta útil para los astrónomos, pero no nos dice nada acerca
de las propiedades intrínsecas de una estrella. Necesitamos establecer
una propiedad común que podamos usar para comparar diferentes estrellas
y para realizar análisis estadísticos. Esta propiedad es la magnitud
absoluta.
La magnitud absoluta, \(M\), se define
como la magnitud relativa que tendría una estrella si fuera colocada a
10 parsecs del Sol (para más información sobre parsecs ver la sección
Herramientas Matemáticas) del Sol.
Ya que hay muy pocas estrellas que estén exactamente a 10 parsecs,
podemos usar una ecuación que nos permitirá calcular la magnitud
absoluta para estrellas a diferentes distancias: la ecuación de
distancia. La ecuación, naturalmente, también funciona en sentido
contrario ? puede calcularse la distancia dada la magnitud absoluta.
\[\begin{aligned} M = m+5-5\log_{10} (D) \end{aligned}\]
Esta ecuación establece la conexión entre la magnitud aparente, \(m\), la magnitud absoluta, \(M\) y la distancia, \(D\), medida en parsec.
Universo, Galaxias y Estrellas
En 1928 Hubble comprobó algo asombroso, salvo las galaxias de nuestro
grupo local, todas presentan un claro efecto Doppler de desplazamiento
al rojo proporcional a la distancia de cada galaxia hasta la
nuestra.
Descomponiendo la luz blanca con un prisma o una red de difracción se
observa el arco iris. Se ha dispersado la luz según su frecuencia: mayor
en el color azul y menor en el rojo.
Si dispersamos de esta forma la luz de una estrella o de una galaxia, se
observan unas líneas negras en el espectro. Corresponden a la absorción
de energía luminosa por sustancias que rodean la fuente luminosa. Estas
rayas son características de los diversos elementos y moléculas y nos
han permitido identificar los componentes de los astros.
En las galaxias distantes Hubble observó claramente el desplazamiento al
rojo que indica que se alejan de nosotros. Más aún, la cuantía del
desplazamiento al rojo es aproximadamente proporcional a la distancia a
que se encuentra la galaxia, que es tanto como decir que la velocidad
con que se alejan de nosotros es proporcional a esa distancia.
Este fenómeno dio pie a la idea de un Universo en expansión a partir de
un estado primitivo de tamaño puntual, densidad infinita y temperatura
extremada. El descubrimiento posterior de una radiación de fondo,
procedente de esa era inicial y las fotos obtenidas desde satélites
espaciales que muestran un Universo más denso, confirman el modelo del
Big Bang.
En el último decenio los astrofísicos han encontrado huellas de una
nueva fuerza fundamental de repulsión entre cuerpos que actuaría a
grandes distancias y sería responsable de que la expansión universal se
esté acelerando.
Galaxias
Una galaxia es un sistema conformado por materia visible en forma de estrellas, gas y polvo interestelar, rodeadas por lo que se conoce como halo de materia oscura. Podemos enunciar así una definición de estos conjuntos y analizar cada frase:
Las galaxias son los agregados de materia gravitacionalmente reunida más grandes del Universo.
materia: estrellas, gas, polvo, agujeros negros, materia oscura,
gravitacionalmente reunida: conforman un conjunto definido de materia en cierto volumen del Universo
más grandes del Universo: tamaños entre 10000 y 200000 años luz con una masa de 1000 a 500000 millones de masas solares en forma de materia visible y otra cantidad mayor de materia oscura.
De acuerdo a su morfología, las galaxias se clasifican en:
Elípticas
Espirales
Irregulares
Estrellas
Las estrellas se forman a partir del colapso gravitatorio de las
nubes moleculares distribuidas en la galaxia que forma parte, las cuales
están formadas principalmente por gas y polvo. Al contraerse, aumenta su
temperatura, hasta que está lo suficientemente elevada como para que
comiencen a tener lugar algunas reacciones termonucleares; como
consecuencia la proto-estrella comienza a irradiar.
La evolución de una estrella pasa por distintas etapas. Suponiendo que
se dan las condiciones necesarias para que comience la etapa de vida de
una estrella, entonces:
Etapa de Pre-Secuencia Principal: Las estrellas se forman a partir del colapso gravitatorio de las nubes moleculares distribuidas en la galaxia que forma parte, las cuales están formadas principalmente por gas y polvo. Al contraerse, aumenta su temperatura, hasta que está lo suficientemente elevada como para que comiencen a tener lugar algunas reacciones termonucleares; como consecuencia la proto-estrella comienza a irradiar. Cuando la presión de radiación logra contrarrestar la contracción gravitatoria (peso de las capas superiores), la estrella llega a la secuencia principal.
Etapa de Secuencia Principal: En esta etapa la estrella pasa la mayor parte de su vida, transformando núcleos de átomos de H en núcleos de He en la zona central de la misma a través de las reacciones termonucleares. Solo el 0,7% del H quemado se convierte en energía nuclear, por lo cual la estrella prácticamente no altera su masa durante mucho tiempo. Sin embargo, en su región central la composición química comienza gradualmente a modificarse a medida que el He se va acumulando en el centro de la estrella.
Etapa de Gigante o Supergigante Roja: Cuando la estrella ha consumido el 10% de su masa de H, se produce una crisis provocada por la acumulación de núcleos de He en el núcleo. La combustión del H continúa en un área brillante que rodea al núcleo. La estrella crece en tamaño y aumenta su brillo, pero la temperatura de las capas externas cada vez más alejadas del núcleo disminuye. La estrella se enfría, enrojece y envejece. Esta fase recibe el nombre de gigante o supergigante roja, según el tamaño de la misma. Cuando la estrella ha consumido aproximadamente el 40% de su masa de H se produce una nueva crisis. El núcleo estelar compuesto de He se contrae por efecto de la gravedad produciendo un aumento de la temperatura en esa región; en esta circunstancia el He comienza a fusionarse, produciendo carbono y oxigeno mediante el proceso llamado “triple alfa”. A medida que la temperatura nuclear crece se producen distintos elementos químicos. Las estrellas de baja masa producen elementos pesados hasta formar un núcleo de Carbono. Las de alta masa continúan produciendo elementos más pesados hasta formar un núcleo de Fe. Las etapas finales de las estrellas van a depender de la masa de estos núcleos.
Etapas finales: Hacen falta valores grandes de densidades para llegar a los llamados “estados de degeneración” de la materia. Para la degeneración de electrones se requerirá de una densidad aproximada de 106 \(g/cm^{3}\) (1000 \(kg/cm^{3}\)) mientras que para la de los neutrones hará falta mucha más aún, aproximadamente 1014 \(g/cm^{3}\) 100.000 Toneladas/cm\(^{3}\). Estos valores, que parecen increíbles, se alcanzan en los núcleos de las estrellas. El límite de Chandrasekhar establece el valor de la masa más allá de la cual la presión del gas electrónico degenerado no es capaz de contrarrestar la fuerza de gravedad, que ocurre principalmente a zona central de la estrellas en evolución. Dicha masa límite es aproximadamente 1,4 veces la masa del Sol (\(M = 1,4 M_{Sol}\)).
Si la estrella llega a la fase en la que se agota su energía nuclear con una masa mayor que \(1,4 M_{Sol}\), la presión del gas de electrones no podrá sostener el colapso. Éste generará una onda de choque y las capas exteriores se expanden. También se eyectan elementos pesados al medio interestelar. El fenómeno conjunto de la explosión y la eyección de material estelar se denomina supernova.
Si luego de la fase de gigante roja el objeto central tenía una masa M tal que \(1,4 M_{Sol} < M < 4,3 M_{Sol}\) finalizará como una estrella de neutrones. En cambio, si su masa \(M > 4.3 M_{Sol}\) lo hará como Agujero Negro. En cambio, si luego de la etapa gigante roja el núcleo de la estrella se encuentra dentro del límite de Chandrasekhar, el objeto final resultante será una enana blanca. Éste será la etapa final de nuestro Sol.
Etapas de la evolución estelar.
Ejercicios
Mercurio tiene una velocidad de 60 km/s cuando pasa por el perihelio a 46 millones de kilómetros del Sol. Debemos calcular:
Velocidad en el afelio, a 70 millones de kilómetros del Sol.
Semieje mayor de su órbita.
El semieje mayor de la órbita de Marte es de 225 millones de km y su periodo es de 1,9 años. Sabiendo que la órbita de Júpiter es casi circular, ¿cuánto valdrá su radio si el periodo es de 11,9 años?
Un satélite geoestacionario (siempre sobre el mismo punto del planeta) está a 36000 km sobre la superficie de la Tierra. ¿Qué periodo tiene otro situado a 3600 km de altura? Radio aproximado de la Tierra: 6400 km.
Calcula la masa del Sol, considerando que la Tierra describe una órbita circular de 150 millones de kilómetros de radio.
La Luna tiene aproximadamente 1/80 de la masa terrestre, mientras que el Sol es aproximadamente 330.000 veces más masivo que nuestro planeta. Por otro lado, la Luna está a unos 380.000 km de la Tierra y el Sol a 150 millones de km Comparemos la fuerza que estos dos astros ejercen sobre nuestro planeta.
Sabiendo que el radio de la Tierra es de unos 6400 km y que la gravedad superficial es de 9,8 m/s\(^{2}\), debemos calcular a qué altura sobre la superficie la gravedad será g= 8,2 m/s\(^{2}\)
Io es un satélite de Júpiter que gira alrededor del planeta en órbitas casi circulares de 422.000 km de radio con un periodo de 42,5 horas. Determinar la masa de Júpiter.
En la película Gravity, ganadora de siete Óscar en 2014, dos astronautas (Sandra Bullock y George Clooney) reparan el telescopio espacial Hubble, que se mueve en una órbita a 593 km sobre el nivel del mar. Para evitar el impacto con los desechos de un satélite, los astronautas se propulsan hacia la Estación Espacial Internacional, que órbita a una altura de 415 km sobre el nivel del mar. Aunque en la realidad no es así, suponemos que las dos órbitas están en el mismo plano, según muestra la ficción de la película. Calcular:
El valor de la gravedad terrestre en el telescopio Hubble.
Los periodos orbitales (en minutos) del telescopio Hubble y de la Estación Espacial.
Un avión de pasajeros vuela a 8 km de altura a una velocidad de 900 km/h. La masa total del avión, contando combustible, equipaje y pasajeros, es de 300000 kg. Calcular:
El valor de la gravedad terrestre en el avión.
La fuerza gravitatoria que ejerce el avión sobre la Tierra
El radio del Sol es de 696000 km y su masa vale \(1,99 \times 10^{30}\) kg.
Calcular:
El valor de la gravedad en la superficie solar.
Si el radio de la órbita de Neptuno alrededor del Sol es 30 veces mayor que el de la órbita terrestre, ¿cuál es el período orbital de Neptuno, en años?
El Sol gira alrededor del centro de la galaxia, situado a 30.000 años-luz en unos 200 millones de años. Los científicos han demostrado que ese movimiento depende tan solo de la masa de la galaxia más cercana al centro que el propio Sol. Intentemos calcular esa masa galáctica.
Un satélite de comunicaciones está en órbita circular geoestacionaria. Debemos calcular su altura sobre la superficie terrestre, recordando que el radio de la Tierra es unos 6400 km y la masa del planeta es aproximadamente \(6\times 10^{24}\) kg
La velocidad de escape de la superficie de la Tierra es 11,3 km/s ¿Cuál será la velocidad de escape de la superficie del planeta Júpiter , cuya masa es unas 300 veces la terrestre y un radio 11 veces mayor que el de la Tierra?
Un agujero negro es un cuerpo tan denso que la velocidad de escape es mayor que la de la luz (\(300000 km/s\)). Para estudiarlos es precisa la teoría de la Relatividad; no obstante, calculemos que diámetro tendría desde el punto de vista clásico un agujero negro con la masa del Sol (\(2\times 10^{30}\) kg). ¿Y con la masa de la Tierra (\(5,98\times 10^{24}\) kg)?
La estrella \(\alpha\)-Orionis (Betelgeuse) tiene una magnitud aparente de m = 0,45 y una magnitud absoluta M = -5,14. Encuentra la distancia a Betelgeuse.
\(\alpha\)-Lyrae (Vega), con una magnitud absoluta de 0,58, está a una distancia de 7,76 parsec. Calcula la magnitud aparente de Vega.
\(\alpha\)-Cygni (Deneb) es la estrella superior izquierda del Triángulo del Verano y es la estrella más brillante de la constelación del Cisne. Su magnitud aparente es 1,25 y la distancia es de 993 parsec. Calcula la magnitud absoluta.
La estrella \(\alpha\)-Canis Majoris (Sirio) es la estrella más brillante del cielo. Está a una distancia de 2,64 parsecs y su magnitud aparente es -1,44. Calcula la magnitud absoluta de Sirio.
La estrella A tiene una magnitud absoluta +5 y la estrella B una magnitud absoluta +10. ¿Cuál afirmación es correcta?
A es más luminosa que B.
B es más luminosa que A.
A está más cercana que B.
B está más cercana que A.
Para dos estrellas A y B se tiene: m\(_{A}\)=5, M\(_{A}\)=4, m\(_{B}\)=10, M\(_{A}\)=11. ¿Cuál afirmación es correcta?
A está más cercana que B.
B está más cercana que A.
A y B se encuentra a igual distancia de la Tierra.
No pueden determinarse las distancias a partir de la información proporcionada.
Dos estrellas tienen la misma magnitud absoluta. Una está 20 veces más lejos que la otra. ¿Cuál es la diferencia entre las magnitudes aparentes?
Una estrella está a 20 pc del Sol y tiene una magnitud aparente +2. ¿Cuál es su magnitud absoluta?
Una estrella tiene una magnitud aparente +9 y una magnitud absoluta +4. ¿A qué distancia se encuentra?
Una estrella cuya magnitud aparente es 12 está ubicada a una distancia de 50 años-luz. ¿Cuál es su magnitud absoluta?
Plutón tiene una masa de \(1,29 \times 10^{22}\) kg, un radio de 1151 km y el radio medio de su órbita alrededor del Sol es de \(5,9 \times 10^{9}\) km.
Calcule \(g\) en la superficie de Plutón.
Su satélite Caronte tiene una masa de \(1,52 \times 10^{21}\) kg y está a 19640 kilómetros de él. Obtenga la fuerza de atracción gravitatoria entre Plutón y Caronte.
Calcule cuántos años tarda Plutón en completar una vuelta alrededor del Sol.
El planeta Júpiter posee un radio 11 veces mayor que el de la Tierra y una masa 318 veces mayor que la de ésta. Calcular:
El peso en Júpiter de un astronauta que en la Tierra pesa 800 N.
La masa del astronauta en Júpiter
La relación entre las velocidades de escape desde la superficie de Júpiter y desde la de la Tierra
Las estrellas \(\zeta\) Per y \(\varepsilon\) Efer tienen magnitudes absolutas 4,54 y 3,23, respectivamente, y tienen magnitudes aparentes iguales. Demuestra que \(\zeta\) Per es más distante que \(\varepsilon\) Efer
Matemática Avanzada
Límite
Punto de Acumulación
Definición 11.1 (Punto de Acumulación). El concepto de punto de acumulación de un conjunto en un espacio captura la noción informal de punto que está arbitrariamente próximo al conjunto sin pertenecer necesariamente a él.
Ejemplo 11.1. El intervalo (0,1) tiene como puntos de acumulación a todos los puntos del intervalo [0,1].
Ejemplo 11.2. Los números naturales no tienen puntos de acumulación.
Límite
Definición 11.2 (Límite). Una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.
La representación numérica del concepto de límite se manifiesta en el cálculo de tablas de valores de la función dada tomando valores tan próximos al punto cómo se quiera y estudiando la tendencia de las imágenes correspondientes.
Ejemplo 11.3. A continuación se presenta un
ejemplo para el cálculo del límite de la función \(f(x)=x^{2}+1\) cuando \(x \rightarrow 1\) y cuando \(x \rightarrow 0\).
| \(x\) | \(f(x)=x^{2}+1\) |
|---|---|
| 2 | 5 |
| 1.5 | 3.25 |
| 1.01 | 2.0201 |
| 1.001 | 2.002001 |
| 1 | 2 |
| 0.9999 | 1.99980001 |
| 0.999 | 1.998001 |
| 0.5 | 1.25 |
| 0.1 | 1.01 |
| 0.001 | 1.000001 |
| 0 | 1 |
\(\blacksquare\)
Ejemplo 11.4. La población de un estado viene dada, en millones de habitantes, por la función:
\[\begin{aligned} P(t)=\frac{20(t-1)}{4+(t-1)^2}+40 \end{aligned}\] donde \(t\) es el tiempo en años. Calcular la población cuando el límite de \(t\) tiende a infinito.
\(\blacksquare\)
Ejemplo 11.5. Luis y María tienen una piscina en su jardín y al llegar el verano necesitan cambiar el agua de la piscina. Abren el desagu?e y la piscina se comienza a vaciar según la función:
\[\begin{aligned} v(t)=\frac{\sqrt{t+3}-2}{t-1} \end{aligned}\] donde \(t\) es el tiempo de vaciado en horas y \(v(t)\) es el volumen de agua expresado en \(m^{3}\). Averigua hacia donde se aproxima el volumen de la piscina cuando el tiempo se aproxima a 1 hora.
\(\blacksquare\)
Derivada
Vamos a estudiar los desplazamiento que realiza un móvil en
determinados intervalos de tiempo. Un móvil es un objeto que se mueve, y
que puede ser un auto, una bicicleta, un barco o cualquier otra
cosa.
Para realizar el estudio del movimiento necesitamos establecer una
referencia, un punto fijo del cual podamos medir distancias y tiempos
(observador). Empecemos a hacer mediciones y observamos que al cabo de 2
segundos el móvil ha recorrido 4 metros. Luego, observamos que al cabo
de 10 segundos el móvil se desplazó 20 metros. Podríamos representar el
resultado diciendo que en el intervalo de tiempo \(t_{2}-t_{1}=10-2\) segundos, se ha
recorrido la siguiente distancia \(x_{2}-x_{1}=20-4\) en metros.
Estas letras se simbolizan mediante la letra griega \(\Delta\) de la siguiente manera:
\[\begin{aligned} \Delta x&=&x_{2}-x_{1} \\ \Delta t&=&t_{2}-t_{1} \end{aligned}\]
Estas diferencias suelen llamarse incrementos.
Si seguimos haciendo mediciones y observaciones que siempre el recorrido
es el doble al tiempo empleado en el mismo, podremos concluir que:
\[\begin{aligned} \Delta x= 2 \cdot \Delta t \end{aligned}\]
O que es lo mismo:
\[\begin{aligned} \frac{\Delta x}{\Delta t}= 2 \end{aligned}\]
Este cociente entre estos incrementos es lo que se denomina velocidad
del móvil, que en este caso es 2 m/s. En particular, dado que ante
cualquier intervalo de tiempo la velocidad es la misma, estamos en
presencia de un movimiento del tipo MRU.
Cuando estamos midiendo la velocidad en un dado intervalo de tiempo, en
realidad lo que estamos calculando es la velocidad media de ese
intervalo de tiempo. La velocidad en un punto es lo que se denomina
velocidad instantánea. Ocurre que si la velocidad es
constante, la velocidad media coincide con la velocidad instantánea. Es
fácil ver que la velocidad es diferente según el ángulo que dicha recta
forme con el eje horizontal en el gráfico espacio-tiempo. Más aún,
cuanto mayor es el ángulo, mayor es la velocidad.
El asunto empieza a complicarse cuando la relación entre el incremento
del espacio y el incremento del tiempo nos es constante. Es decir,
cuando el gráfico espacio-tiempo no es una función lineal, tal como
sucede en en la figura 11.1.
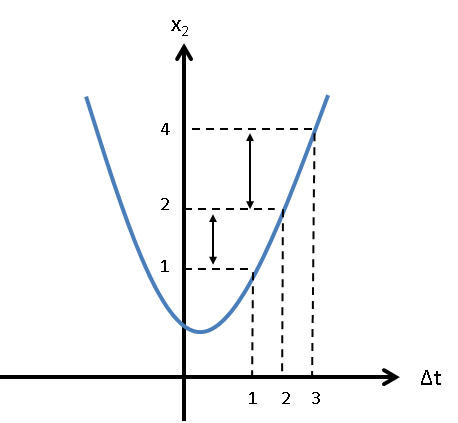 |
En este caso la velocidad media del móvil varía según el intervalo de
tiempo que se esté analizando. Lo que todavía no podemos calcular es la
velocidad instantánea del móvil para un dado tiempo, por ejemplo para
\(t=1,5\) segundos. Aunque podríamos
considerar un intervalo muy pequeño en torno a \(t=1,5\) y obtener así un valor aproximado
de dicha velocidad. Cuanto menor sea el intervalo mejor será la
aproximación.
Lo que decimos es que el cociente de los incrementos \(\Delta x/\Delta t\) se aproxima mejor a lo
que decimos velocidad instantánea cuando es más pequeño es el incremento
\(\Delta t\), como consecuencia, la
velocidad instantánea se definirá como:
\[\begin{aligned} v=\lim_{ \Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} \end{aligned}\]
Definición 11.3 (Derivada). La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
Vamos ahora a abandonar los móviles y a plantear el asunto en término
geométricos. Dando valores a \(x\) se
obtienen los correspondientes valores de \(y\), como puede observarse en la figura 11.1.
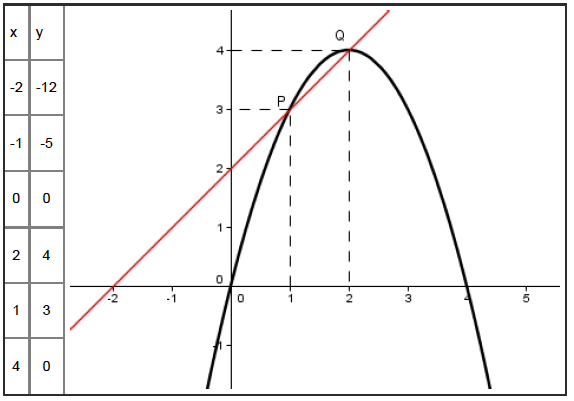 |
Por otro lado, recordemos que la ecuación de una recta tiene la forma \(y = mx + b\). Vamos a calcular la ecuación de la recta que pasa por los puntos \(P(1, 3)\) y \(Q(2, 4)\). Sustituyendo dichos puntos en la ecuación de la recta nos queda:
\[\begin{aligned} 3 &=& m + b \\ 4 &=& 2m + b \end{aligned}\]
Sistema de dos ecuaciones con dos incógnitas que nos permitirá
obtener los valores de \(m\) y \(b\). Despejando m de la primera ecuación
tenemos que \(m = 3 -b\), y
sustituyéndola en la segunda, \(4 = 2(3 -b)+ b
= 6 - 2b+ b = 6- b\); con lo que \(b =
6 - 4= 2\). Sustituyendo este valor de b en la primera nos da 3 =
m + b, con lo que m = 1.
En definitiva, la ecuación de la recta es \(y
= x + 2\) (ver figura 11.2).
Recordemos que en la ecuación \(y = mx +
b\), \(m\) es lo que se llama la
pendiente de la recta y representa el ángulo que ésta forma con el eje
de abscisas, o más exactamente, la tangente trigonométrica de dicho
ángulo, al que podemos llamar \(\alpha\). De manera que \(m = \tan \alpha\).
En la recta cuya ecuación acabamos de calcular, se tiene que la
pendiente vale 1 (\(m =1\)), es decir,
que \(\tan \alpha = 1\), por lo que
\(\alpha = 45º\).
Ecuación de la tangente
El problema que nos planteamos ahora, y que trajo de cabeza a decenas
de matemáticos ilustres durante siglos, es cómo hallar la ecuación de la
recta tangente a una curva en uno cualquiera de sus puntos.
Volvamos a la curva \(y =- x^{2}+ 4x\)
que hemos estado utilizando hasta ahora, y tratemos de encontrar la
ecuación de la recta tangente a la misma en el punto de abscisa \(x = 1\). Hemos visto que encontrar la recta
que pasa por los puntos \(P(1, 3)\) y
\(Q(2, 4)\) no representaba ningún
problema. Hagamos ahora retroceder el punto \(x = 2\) hacia la izquierda, de manera que
el punto \(Q\) que está sobre la curva
se vaya aproximando a \(P\) (ver figura
11.3).
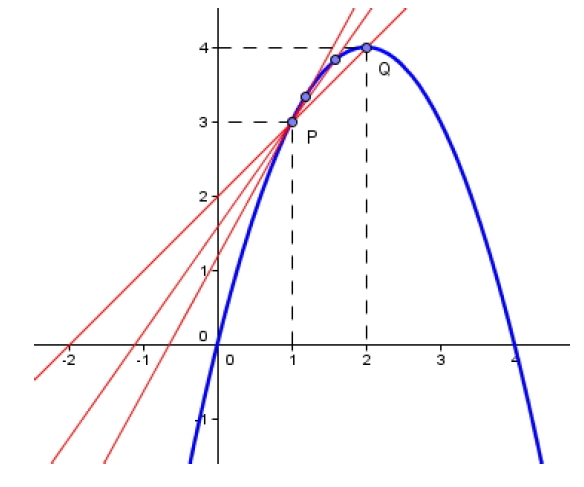 |
Observamos cómo la pendiente de las sucesivas rectas que obtenemos va
aumentando. ¿Qué sucederá en el momento en que el punto \(Q\) alcance la posición del punto \(P\)? Pues que la recta que se estaba
moviendo y que cortaba a la curva en dos puntos la cortará en uno solo,
es decir, que se habrá convertido en la recta tangente.
Lo que debemos hacer ahora es ver cómo evolucionan las pendientes de las
rectas hasta convertirse en la pendiente de la recta tangente, y lo
vamos a hacer en el caso más general para un punto \(P(x, y)\) cualquiera de la curva.
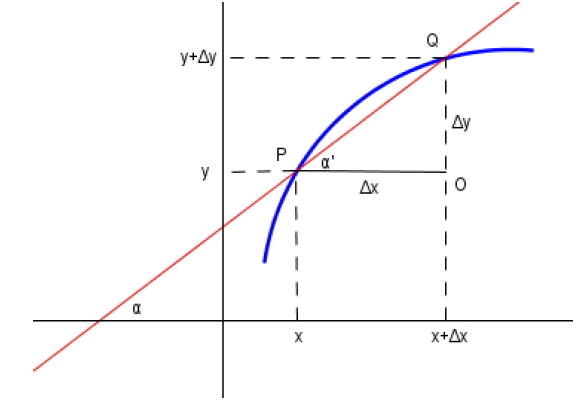 |
Vemos que los ángulos \(\alpha\)
(pendiente de la recta) y \(\alpha\)’
son iguales. Recordemos que la pendiente es la tangente trigonométrica
de dicho ángulo.
Reparemos un momento en una cuestión que se puede prestar a confusión,
que es la del empleo del término tangente en dos acepciones diferentes:
una es la tangente a la curva, en la que hablamos de una recta y es una
acepción puramente geométrica; la otra es la tangente de un ángulo,
cuando nos referimos a la pendiente, y ésta es una acepción
trigonométrica.
Volvamos a la figura y calculemos el valor de la tangente trigonométrica
(ver figura 11.4). Es decir:
\[\begin{aligned} \tan \alpha=\tan \alpha'=\frac{QO}{PO}=\frac{(y+\Delta y)-y}{(x+\Delta x)-x}=\frac{\Delta y}{\Delta x} \end{aligned}\]
De forma que las pendientes de todas las rectas que cortan a la curva en los puntos \(P\) y \(Q\) pueden venir dadas por el cociente incremental. Pero, ¿qué significa que el punto \(Q\) retrocede hacia el \(P\)?, pues que \(\Delta x\) va haciéndose cada vez más pequeño, luego el valor de la pendiente que buscamos estará en el límite en que dicho valor sea \(0\):
\[\begin{aligned} f'(x)=m&=&\lim_{\Delta x\rightarrow 0} \frac{\Delta y}{\Delta x} \nonumber \\ &=& \lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x}{\Delta x} \end{aligned}\] que es precisamente la definición de derivada de una función en un punto y que se representa colocando un apóstrofo en la letra \(f\) que utilizamos para representar la función.
Máximos y Mínimos
Cuando la pendiente \(m\) de una
recta es positiva, el ángulo que ésta forma con el eje horizontal está
comprendido entre 0º y 90º, cuando es negativa, entre 90º y 180º (ver
figura 11.5).
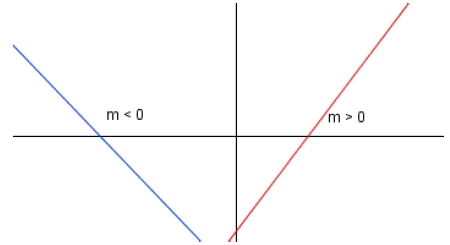 |
Hemos visto la relación que guardaba dicha pendiente con la derivada
a una curva en uno de sus puntos. Por lo tanto, cuando la derivada de
una función en un punto sea positiva significa que las rectas tangentes
se inclinan hacia la derecha, que es tanto como afirmar que la curva
“sube”, es decir, que es creciente. Recíprocamente, en aquellos
intervalos en los que la derivada sea negativa, la curva será
descendiente.
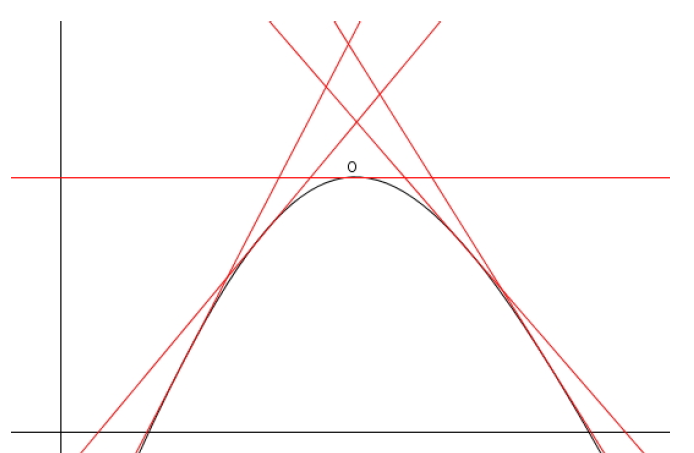 |
En un punto tal como \(O\), la
derivada es cero, por lo que el ángulo que forma la tangente a la curva
en ese punto con la horizontal también vale \(0\). Ésta es una condición necesaria (no
siempre suficiente) para que en dicho punto exista un máximo local (ver
figura 11.6).
Evidentemente, todo lo dicho es válido para la presencia de un mínimo
local.
Derivada de un polinomio y una constante
Vamos a ver dos casos especiales de derivadas, el de una función polinómica o exponencial y el de una constante.
La derivada de una potencia o función potencial (polinomio), es igual al exponente por la base elevada al exponente menos uno, es decir:
\[\begin{aligned} f(x)&=&ax^{n} \\ f'(x)&=&n\cdot ax^{n-1} \end{aligned}\]
En en el caso de una función constante, la derivada siempre toma el valor cero, es decir:
\[\begin{aligned} f(x)&=&K \\ f'(x)&=&0 \end{aligned}\]
Regla de la Derivada de una Suma y Resta de funciones
La derivada de una suma de dos funciones es igual a la suma de las derivadas de dichas funciones. Es decir:
\[\begin{aligned} f'(x)=g'(x)\pm h'(x) \end{aligned}\]
Ejemplo 11.6. Calcular la derivada de la siguiente función:
\[\begin{aligned} f(x)=3x^{2}-5x+2 \end{aligned}\]
Aplicando la regla de derivación de un polinomio y la regla de suma de funciones, tenemos que la derivada es:
\[\begin{aligned} f'(x)&=&2\cdot 3x^{2-1}-1\cdot 5x^{1-1}+0 \\ f'(x)&=&6x-5 \end{aligned}\]
\(\blacksquare\)
Aplicación a la cinemática
Recordemos algunas definiciones:
Definición 11.4 (Velocidad Instantánea). Se define como velocidad instantánea a la derivada de la función del espacio del objeto o móvil. Por lo tanto, \[\begin{aligned} v=x'(t) \end{aligned}\]
Definición 11.5 (Aceleración Instantánea). Se define como aceleración instantánea a la derivada de la función de la velocidad del objeto o móvil. Por lo tanto, \[\begin{aligned} a=v'(t) \end{aligned}\]
Definición 11.6 (Velocidad Media). \[\begin{aligned} v=\frac{\Delta x}{\Delta t} \end{aligned}\]
Definición 11.7 (Aceleración Media). \[\begin{aligned} a=\frac{\Delta v}{\Delta t} \end{aligned}\]
Ejemplo 11.7. Un móvil sigue una trayectoria en el espacio según la siguiente ecuación:
\[\begin{aligned} x(t)=5t^{3}-2t^{2}+7t+15 \end{aligned}\] donde \(x\) representa el espacio medido en metros y \(t\) el tiempo medido en segundos. Calcular:
La velocidad y aceleración instantánea a los 7 y 10 segundos
La velocidad y aceleración media en ese intervalo de tiempo
Velocidad máxima / mínima
Para calcular la velocidad instantánea vamos a sacar la derivada de la función del espacio,
\[\begin{aligned} v(t)&=&x'(t)=3\cdot 5t^{3-1}-2 \cdot 2t^{2-1}+1 \cdot 7t^{1-1}+0 \\ v(t)&=&15t^{2}-4t+7 \end{aligned}\]
Luego evaluamos la velocidad instantánea en \(t\) igual a 7 y 10 segundos:
\[\begin{aligned} v(t)&=&15 \cdot 7^{2} - 4\cdot 7 +7=714 m/s \\ v(t)&=&15 \cdot 10^{2} - 4\cdot 10 +7=1467 m/s \end{aligned}\]
Para la aceleración instantánea tenemos que derivar la función de la velocidad \(v(t)=15t^{2}-4t+7\), es decir:
\[\begin{aligned} a(t)&=&v'(t)=2 \cdot 15t^{2-1}-1\cdot 4t^{1-1}+0 \\ a(t)&=&30 t-4 \end{aligned}\]
Ahora, evaluando la función de la aceleración en 7 y 10 segundos tenemos:
\[\begin{aligned} a(t)&=&30 \cdot 7-4=206 m/s^{2} \\ a(t)&=&30 \cdot 10-4=296 m/s^{2} \end{aligned}\]
Para calcular la velocidad media se debe aplicar la definición anterior, es decir:
\[\begin{aligned} v=\frac{\Delta x}{\Delta t}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}} \end{aligned}\] donde \(x_{2}\) y \(x_{1}\) son los espacios recorridos en 10 y 7 segundos respectivamente. Es decir:
\[\begin{aligned} x(t=10s)&=&5\cdot 10^{3}-2\cdot 10^{2}+7 \cdot 10+15=4885 m \\ x(t=7s)&=&5\cdot 7^{3}-2\cdot 7^{2}+7 \cdot 7+15=1681 m \end{aligned}\]
Por lo tanto, la velocidad media es igual a:
\[\begin{aligned} v=\frac{\Delta x}{\Delta t}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{4885m-1681m}{10s-7s}=1068 m/s \end{aligned}\]
De forma similar, la aceleración media nos queda:
\[\begin{aligned} a=\frac{\Delta v}{\Delta t}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{1467 m/s-714 m/s}{10s-7s}=251m/s^{2} \end{aligned}\]
Por último, para calcular la velocidad máxima o mínima, debemos calcular las raíces de la derivada de la velocidad, es decir:
\[\begin{aligned} v'(t)&=&30 t-4=0 \\ t&=&\frac{4}{30}=0,133 s \end{aligned}\]
Esta raíz nos dice en que momento se produce la máxima o mínima velocidad. Ahora bien, reemplazando ese valor en la función de la velocidad instantánea, podemos calcular el valor de la velocidad máxima/mínima:
\[\begin{aligned} v(t)&=&15t^{2}-4t+7 \\ v(t)&=&15 \cdot 0,133^{2}-4 \cdot 0,133 +7=6,73 m/s \end{aligned}\]
Para determinar si es un máximo o un mínimo hay que calcular la derivada de la derivada (derivada segunda), evaluar la función en el punto calculado anteriormente, y si es positivo el resultado es un mínimo; y si es negativo un máximo. Calculemos la derivada segunda:
\[\begin{aligned} v'(t)&=&30 t-4=0 \\ v''(t)&=&30>0 \end{aligned}\]
Como la derivada segunda es siempre mayor que cero, entonces el resultado de la velocidad igual a \(6,73 m/s\) es la velocidad mínima que tiene el móvil durante toda la trayectoria que recorre.
\(\blacksquare\)
Ejercicios
Una empresa tiene capacidad de producir como máximo 15.000 unidades al mes de cierto producto. El costo total de producción \(C_{t}\) en miles de dólares por mes responde a la expresión
\[\begin{aligned} C_{t}(q)=\frac{1}{3}q^{3}-\frac{15}{2}q^{2}+36q+81 \end{aligned}\] donde \(q\) es el número de unidades producidas en miles de unidades por mes. Determina la producción mensual de la empresa que minimiza el costo total de producción y calcula ese costo.
El costo total \(C\) de construcción de un edificio de \(n\) pisos está expresado por:
\[\begin{aligned} C(n)=2n^{2}+300n+320 \end{aligned}\]
Calcula el número de pisos a construir para que el costo total sea mínimo (el resultado deberá ser un número entero).
El Ministerio de Transporte con el fin de determinar la variación de la velocidad del flujo de vehículos que provenientes del Este regresan a Montevideo los días domingos entre las 17:00 horas y las 22:00 horas, ha efectuado mediciones que indican que la velocidad del tránsito a la entrada de la capital en ese lapso esta dada aproximadamente por la expresión:
\[\begin{aligned} V(t)=\frac{80}{9}(\frac{t^{3}}{3}-\frac{5}{2}t^{2}+4t)+\frac{1180}{27} \quad km/h \end{aligned}\]
¿En qué momento entre las 17:00 horas y las 22:00 horas el tránsito es más rápido y en qué momento es más lento?
La velocidad (en m/s) que alcanza cierto atleta en una carrera de 200 metros viene dado en función del tiempo, \(t\), y se representa por la siguiente ecuación: \[v(t) =-0,00055 t \cdot (t-300)\]
Calcular: ¿Cuál es ésta velocidad? ¿en qué tiempo la alcanza?
Calcular los siguientes límites:
\[\lim_{x \rightarrow \infty} \frac{2x^{2}+5x-3}{3x^{2}}\]
\[\lim_{x \rightarrow 0} \frac{3x^{3}-2x}{4x^{2}-x}\]
\[\lim_{x \rightarrow \infty} \frac{x^{3}+5x-3}{x^{4}}\]
\[\lim_{x \rightarrow \infty} \frac{7x^{2}-2x+15}{3x^{2}-x}\]
La siguiente función de espacio representa el recorrido en función del tiempo que realiza un ciclista:
\[x(t)=0,12 \cdot t^{4}-t^{3}+2\cdot t^{2}+5\cdot t+0.1\] donde \(x(t)\) es el espacio recorrido en el tiempo \(t\) medido en km, y \(t\) es el tiempo medido en horas.
Calcular:
El espacio recorrido a las 3 y 12 horas
La velocidad y aceleración instantánea a las 3 y 12 horas
Un persona quiere emprender una aventura en auto. Para ello recorre Argentina de Norte a Sur, cuya función de espacio es la siguiente:
\[x(t)=-3\times 10^{-6} t^{5}+0.00105833 t^{4} -0.12985 t^{3}+6.0105 t^{2}\] donde \(x(t)\) es el espacio recorrido en el tiempo \(t\) medido en km, y \(t\) es el tiempo medido en horas.
Calcular:
El espacio recorrido a las 24 y 60 horas
La velocidad y aceleración instantánea a las 24 y 60 horas
La velocidad y aceleración media entre las 24 y 60 horas
Física I, Resnick and Halliday Vol 1
Aportes para la Enseñanza de la Astronomía en el Secundario, Observatorio Astronómico de Córdoba Universidad Nacional de Córdoba
La Astronomía y su Enseñanza en la Educación Secundaria, Observatorio Astronómico de Córdoba Universidad Nacional de Córdoba
Asimov http://www.asimov.com.ar