Estadística Aplicada
Principales Conceptos Teóricos y
Problemas Resueltos
Aplicaciones en Python
Giuliodori, David Augusto
ISBN 978-987-88-5778-7
Notaciones y Acrónimos
Parámetros y Estimadores
La siguiente tabla resume la simbología para los parámetros poblacionales y sus correspondientes estimadores muestrales.
| Concepto | Parámetro (Población) | Estimador (Muestra) |
|---|---|---|
| Media | \(\mu\) | \(\overline{X}\) |
| Varianza | \(\sigma^{2}\) | \(S^{2}\) |
| Covarianza entre \(X\) e \(Y\) | COV(X,Y) | Cov(X,Y) |
| Proporción | \(\pi\) | \(P\) |
| Diferencia de medias | \(\delta\) | \(d\) |
| Coeficiente de correlación | \(\rho\) | \(r\) |
| Término de error/Residuos | \(\epsilon\) | \(e\) |
| Coeficientes de Regresión Lineal | \(\beta_{i}\) | \(b_{i}\) |
Símbolos Matemáticos
\(\in\) Pertenece
\(\sim\) Se distribuye
\(\Rightarrow\) Implica
\(\mathbb{R}\) Conjunto de números reales
\(\vee\) Unión
\(E(.)\) Operador esperanza
\(V(.)\) Operador varianza
Int(.) Parte entera de un número
\(f^{o}\) Frecuencias Observadas
\(f^{e}\) Frecuencias Esperadas
Nomenclatura General
- Variable aleatoria: Letras latinas en mayúscula (ej: \(X\)).
- Observación muestral: Letras latinas en minúscula (ej: \(x_{i}\) es la i-ésima observación).
- Unidad de medida: Corchetes (ej: \([X]\) es la unidad de la variable \(X\)).
Acrónimos
- ANOVA: Analysis of Variance (Análisis de la Varianza)
- CMD: Cuadrado Medio Dentro de los grupos
- CME: Cuadrado Medio Entre grupos
- CMT: Cuadrado Medio Total
- CO: Curva Característica de Operación
- DW: Estadístico de Durbin-Watson
- EMV: Estimador por Máxima Verosimilitud
- MAS: Muestreo Aleatorio Simple
- MCO: Mínimos Cuadrados Ordinarios
- ME: Muestreo Estratificado
- SCD: Suma de los Cuadrados Dentro de los grupos
- SCE: Suma de los Cuadrados Entre grupos
- SCT: Suma de los Cuadrados Totales
- TAVN: Teorema de Adición de Variables Normales
- TCL: Teorema Central del Límite
- ZR: Zona de Rechazo
Introducción
En estadística inferencial desempeñan un rol fundamental las distribuciones de probabilidad y el Teorema Central del Límite, que están estrechamente ligados a los conceptos de muestra, parámetro, estadístico y estimador, cuya definición rigurosa se introduce en la parte pertinente del libro, donde son abordados. A continuación incluimos una noción de cada uno de esos cuatro conceptos, a fin de facilitar la correcta comprensión de los temas en los que es necesario utilizarlos antes de ser debidamente definidos.
Muestra aleatoria simple es aquella que surge de utilizar un procedimiento de selección en el que ningún elemento de la población tiene más posibilidad que otro de ser elegido.
Parámetro es una medida (de posición, variabilidad, asimetría, etc) calculada con los elementos de la población.
Estadístico es una medida (de posición, variabilidad, asimetría, etc) calculada con los elementos de la muestra.
Estimador es un estadístico con una forma funcional particular que se usa para estimar un parámetro de la población, el cual suele ser desconocido. Para cada parámetro poblacional se puede construir un estimador, y pueden existir varios estimadores diferentes para el mismo parámetro.
En el primer capítulo abordaremos el tratamiento de algunas de las distribuciones más importantes del muestreo. Lo iniciaremos con la consideración de un teorema que nos permitirá plantear la distribución del estadístico que más se suele utilizar, esto es, la media muestral (o, en su caso, la proporción muestral). Ese teorema se denomina Teorema Central del Límite (TCL).
Teorema Central del Límite
Consideremos una suma de \(k\) variables aleatorias estadísticamente independientes que provienen de diferentes poblaciones, con distribuciones cualesquiera. Supongamos que dichas variables las representamos por:
\[\begin{aligned} X_{1},X_{2},\cdots ,X_{k} \nonumber \end{aligned}\] a sus medias o valores esperados por:
\[\begin{aligned} \mu_{1},\mu_{2},\cdots ,\mu_{k} \nonumber \end{aligned}\] y a sus correspondientes varianzas mediante
\[\begin{aligned} \sigma_{1}^{2},\sigma_{2}^{2},\cdots ,\sigma_{k}^{2} \nonumber \end{aligned}\]
Entonces, el Teorema Central del Límite expresa que la suma de esas \(n\) variables independientes provenientes de poblaciones con distribuciones cualesquiera tiende a distribuirse normalmente, a medida que \(k\) crece, con media igual a la suma de las medias y varianza igual a la suma de las varianzas. Es decir,
\[\begin{aligned} \sum_{i=1}^{k} X_{i} \sim N(\sum_{i}^{k} \mu_{i},\sum_{i}^{k} \sigma_{i}^{2}) \end{aligned}\]
El TCL justifica que se emplee la distribución normal para realizar inferencias estadísticas y también para llevar a cabo contrastes de hipótesis, todo ello sin necesidad de conocer, de antemano, el proceso que genera los datos.
Aplicaciones del Teorema Central del Límite
Media Muestral
Sean \(X_{1},X_{2} \cdots X_{n}\) variables aleatorias, idénticas e independientemente distribuidas, proveniente de una única población de variable \(X\), con media \(\mu\) y varianza \(\sigma^{2}\). Entonces, aplicando el TCL se cumple, cuando \(n\) es grande, que:
\[\begin{aligned} \overline{X} \sim N(\mu,\sigma^{2}/n) \end{aligned}\]
Lo que es equivalente a:
\[\begin{aligned} \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1) \end{aligned}\]
Esto se debe a que la media muestral \(\overline{X}\) es el resultado de sumar las \(n\) variables divididas, cada una de ellas, por la constante \(n\). Esta suma de variables se distribuye normal con parámetros \(\mu\) y \(\frac{\sigma^{2}}{n}\), tal como se puede apreciar:
\[\begin{aligned} \overline{X}=\frac{\sum_{i=1}^{n}X_{i}}{n}=\frac{X_{1}}{n}+\frac{X_{2}}{n}+\cdots+\frac{X_{n}}{n} \end{aligned}\] por lo tanto \[\begin{aligned} E(\overline{X})\!=\; & E(\frac{X_{1}}{n}+\frac{X_{2}}{n}+\cdots+\frac{X_{n}}{n}) \nonumber \\ \!=\; & \frac{1}{n}(E(X_{1})+E(X_{2})+\cdots+E(X_{n}))=\frac{1}{n}n\mu=\mu \end{aligned}\] y para la varianza \[\begin{aligned} V(\overline{X})\!=\; & V\Big(\frac{\sum_{i=1}^{n}X_{i}}{n}\Big) \nonumber \\ \!=\; & \frac{1}{n^{2}}V\Big(\sum_{i=1}^{n}X_{i}\Big) \nonumber \\ \!=\; & \frac{1}{n^{2}}(V(X_{1})+V(X_{2})+\cdots+V(X_{n})=\frac{1}{n^{2}}n\sigma^{2}=\frac{\sigma^{2}}{n} \end{aligned}\]
En el caso de variables provenientes de distribuciones normales, la media muestral se distribuye normalmente, cualquiera sea el tamaño de muestra \(n\), por el Teorema de Adición de Variables Normales (TAVN). En efecto, si se tienen \(X_{1}, \cdots X_{n}\) variables aleatorias normales, idéntica e independientemente distribuidas, con medias \(\mu_{i}\) y varianzas \(\sigma_{i}^{2}\), se cumple que \(\overline{X}\) es siempre normal, ya sea por aplicación del TCL (y también por el TAVN) si \(n\) es grande, o por el TAVN si \(n\) es pequeño.
Proporción Muestral
Sean \(X_{1}, \cdots X_{n}\) variables aleatorias, idéntica e independientemente distribuidas provenientes de una distribución dicotómica (Bernoulli). El estadístico proporción muestral se define como:
\[\begin{aligned} P=\frac{\sum_{i}^{n}X_{i}}{n} \end{aligned}\] es decir que \(P\) no es más que \(\overline{X}\) cuando la distribución de cada una de las \(n\) variables es Bernoulli. Recordemos que para la distrbución de Bernoulli \(E(X)=\pi\) y que \(V(X)=\pi(1-\pi)\). Entonces, se cumple, por el TCL, que cuando \(n\) es lo suficientemente grande:
\[\begin{aligned} P \sim N(\pi,\pi(1-\pi)/n) \end{aligned}\]
Distribuciones derivadas de la Normal
Uno de los objetivos de la Estadística es conocer información relevante de los parámetros poblacionales de una o más distribuciones: la media (\(\mu\)), la varianza (\(\sigma^{2}\)) o la proporción (\(\pi\)). En la práctica escasas veces conoceremos estos valores, por lo que es necesario extraer una muestra aleatoria simple de la población y calcular el valor del estimador, por ejemplo, la media muestral (\(\overline{X}\)), la varianza muestral (\(S^{2}\)) o la proporción muestral (\(P\)), que permita hacer inferencia acerca del respectivo parámetro poblacional. El valor del estimador es aleatorio porque depende de los elementos que se presenten en la muestra seleccionada y, por lo tanto, tiene una distribución de probabilidad asociada. El estudio de estas distribuciones es necesario para entender el proceso de inferencia estadística que será discutido posteriormente. A continuación veremos tres de esas distribuciones muestrales.
Distribución Chi\(^{2}\)
Supongamos que hay \(n\) variables aleatorias independientes \(Z_{i}\), todas con distribución \(N(0,1)\), entonces se define la variable aleatoria \(\chi^{2}\) (denominada chi-cuadrado) como:
\[\begin{aligned} \chi^{2}_{n}\!=\; & \sum^{n}_{i=1}{Z^{2}_{i}} \nonumber \\ \!=\; & \sum^{_n}_{i=1}\bigg(\frac{X_{i}-\mu}{\sigma}\bigg)^{2} \end{aligned}\] donde \(n\) representa los grados de libertad1, es decir la cantidad de valores de \(X\) que son independientes.
Dado que generalmente no se conoce \(\mu\), entonces en la estandarización se pierde un grado de libertad al trabajar con \(\overline{X}\) en lugar de \(\mu\), por lo tanto:
\[\begin{aligned} \chi^{2}_{n-1}\!=\; & \sum^{n}_{i=1}\bigg(\frac{X_{i}-\overline{x}}{\sigma}\bigg)^{2} \end{aligned}\]
Sabiendo que:
\[\begin{aligned} S^{2}=\sum^{n}_{i=1} \frac{(X_{i}-\overline{X})^{2}}{n-1} \end{aligned}\] podemos escribir el estadístico \(\chi^{2}\) como
\[\label{estadistico_chi} {\chi^{2}_{n-1}=\frac{(n-1)S^{2}}{\sigma^{2}}}\]
\(\chi^{2}\) tiene una distribución de probabilidad definida positiva, asimétrica que tiende a ser simétrica a medida que aumentan los grados de libertad.
Por otra parte, haciendo uso de la función generadora de momentos de esta distribución \(\chi^{2}\):
\[\begin{aligned} M_{X}(t)=(1-2t)^{-r/2} \quad \forall \quad t<1/2 \end{aligned}\] donde \(r\) representa los grados de libertad (\(n-1\)), podemos calcular los momentos derivando sucesivamente esta función y evaluando dicha derivada en \(t=0\). Con la derivada primera tenemos:
\[\begin{aligned} E(X^{k})=\frac{d^{k}M_{X}(t)}{dt^{k}}\bigg |_{t=0} \end{aligned}\]
Para obtener el primer momento esperanza tomamos \(k=1\):
\[\begin{aligned} E(X)\!=\; & \frac{d M_{X}(t)}{dt}\bigg |_{t=0} \nonumber \\ \!=\; & r(1-2t)^{-r/2-1}\bigg |_{t=0}=r \end{aligned}\]
Para el segundo momento tomamos \(k=2\):
\[\begin{aligned} E(X^{2})\!=\; & \frac{d^{2}M_{X}(t)}{dt^{2}}\bigg |_{t=0} \nonumber \\ \!=\; & (-2) (-r/2-1) r(1-2t)^{-r/2-2}\bigg |_{t=0}=r^{2}+2r \end{aligned}\] y así sucesivamente para los otros momentos.
La varianza es:
\[\begin{aligned} V(X)\!=\; & E(X^{2})-E(X)^{2} \nonumber \\ \!=\; & r^{2}+2r - r^{2}=2r \end{aligned}\]
Problema Resuelto 1.1. Graficar en Python las distribuciones \(\chi^{2}\) de 3 y 8 grados de libertad y analizar las diferencias que hay entre ellas.
Solución
Lo primero que debemos hacer es importar las librerías de Python necesarias para poder hacer los gráficos2. Posteriormente, asignamos los grados de libertad de cada una de las distribuciones en las distintas variables definidas en el código, en este caso \(df\) y \(df2\).
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from scipy.stats import norm
# Graficando Chi
df = 3 # grados de libertad de la primera funcion
df2 = 8 # grados de libertad de la segunda funcion
chi = stats.chi2(df)
chi2 = stats.chi2(df2)
x = np.linspace(chi2.ppf(0.01),
chi2.ppf(0.99), 100)
x = np.arange(0., 30., 0.001)
# Funcion de Densidad
fp = chi.pdf(x)
fp2 = chi2.pdf(x)
plt.plot(x, fp)
plt.plot(x, fp2)
plt.plot(x, fp,label=r'$\chi^{2}_{3}$',color='tab:orange')
plt.plot(x, fp2,label=r'$\chi^{2}_{8}$', color='tab:blue')
plt.title(r'Distribucion $\chi^{2}$')
plt.ylabel('Densidad')
plt.xlabel('r'$\chi^{2}$')
plt.legend()
plt.show()
plt.savefig('chi2.png')El gráfico que se obtiene (se guarda como archivo de imagen con extensión png), viene dado por:
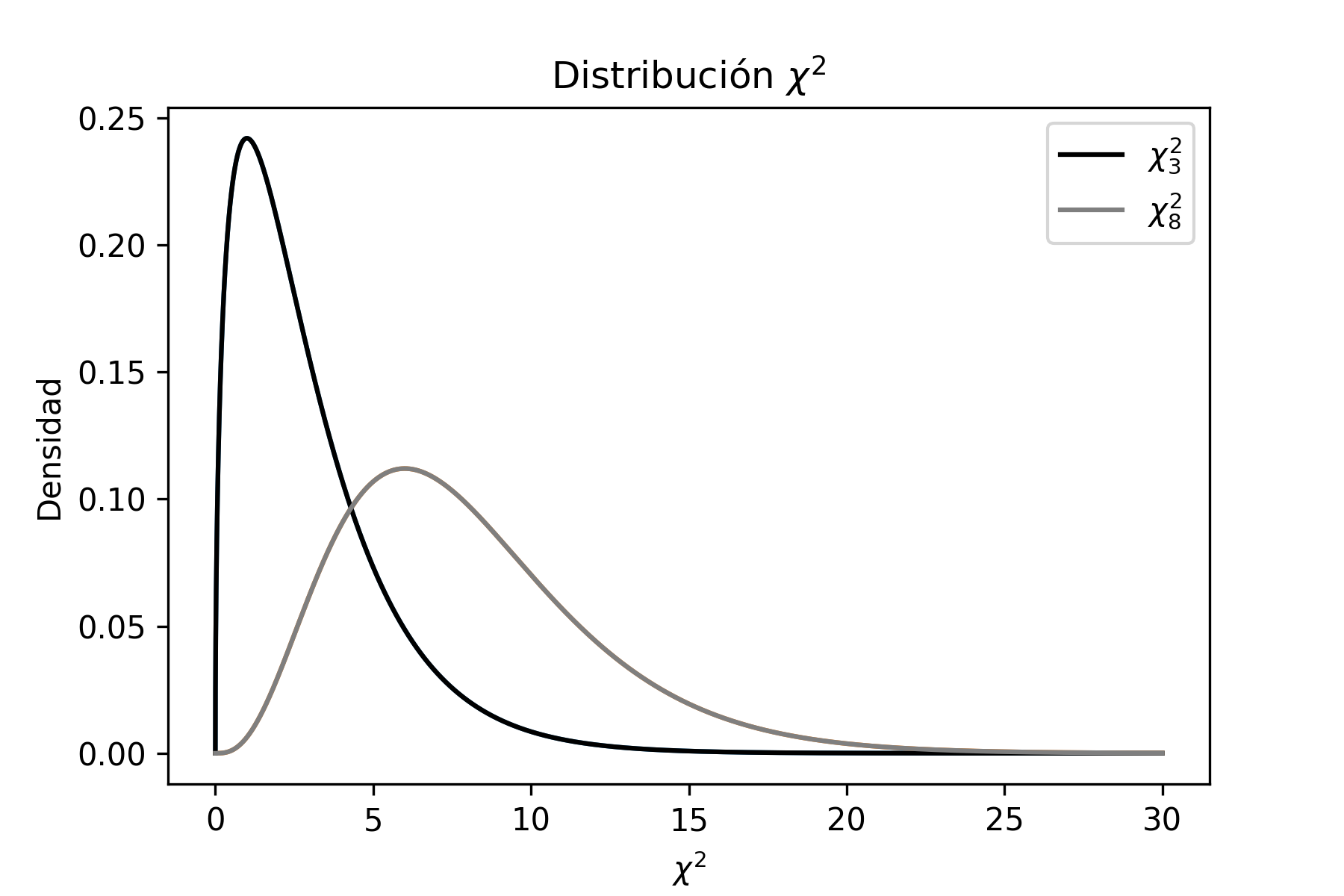
donde se observa que, a medida que los grados de libertad aumentan, la distribución se vuelve más simétrica.
Distribución F
Sean \(U\) y \(V\) dos variables aleatorias que se distribuyen \(\chi^{2}\) con \(n_{1}-1\) y \(n_{2}-1\) grados de libertad respectivamente, entonces:
\[\begin{aligned} U &\sim & \chi^{2}_{n_{1}-1} \nonumber \\ V &\sim & \chi^{2}_{n_{2}-1} \end{aligned}\]
Se define la distribución \(F\) como:
\[\begin{aligned} F_{n_{1}-1,n_{2}-1}=\frac{\frac{U}{n_{1}-1}}{\frac{V}{n_{2}-1}}=\frac{ \frac{\frac{(n_{1}-1)S_{1}^{2}}{\sigma_{1}^{2}}}{n_{1}-1}} {\frac{\frac{(n_{2}-1)S_{2}^{2}}{\sigma_{2}^{2}}}{n_{2}-1}} \nonumber \end{aligned}\] \[\label{estadistico_f1} {F_{n_{1}-1,n_{2}-1}=\frac{S_{1}^{2}}{S_{2}^{2}}\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}}}\]
La distribución \(F\) es una distribución definida positiva y asimétrica que, a medida que aumentan los grados de libertad del numerador y del denominador, tiende a perder la asimetría, es decir tiende a ser simétrica.
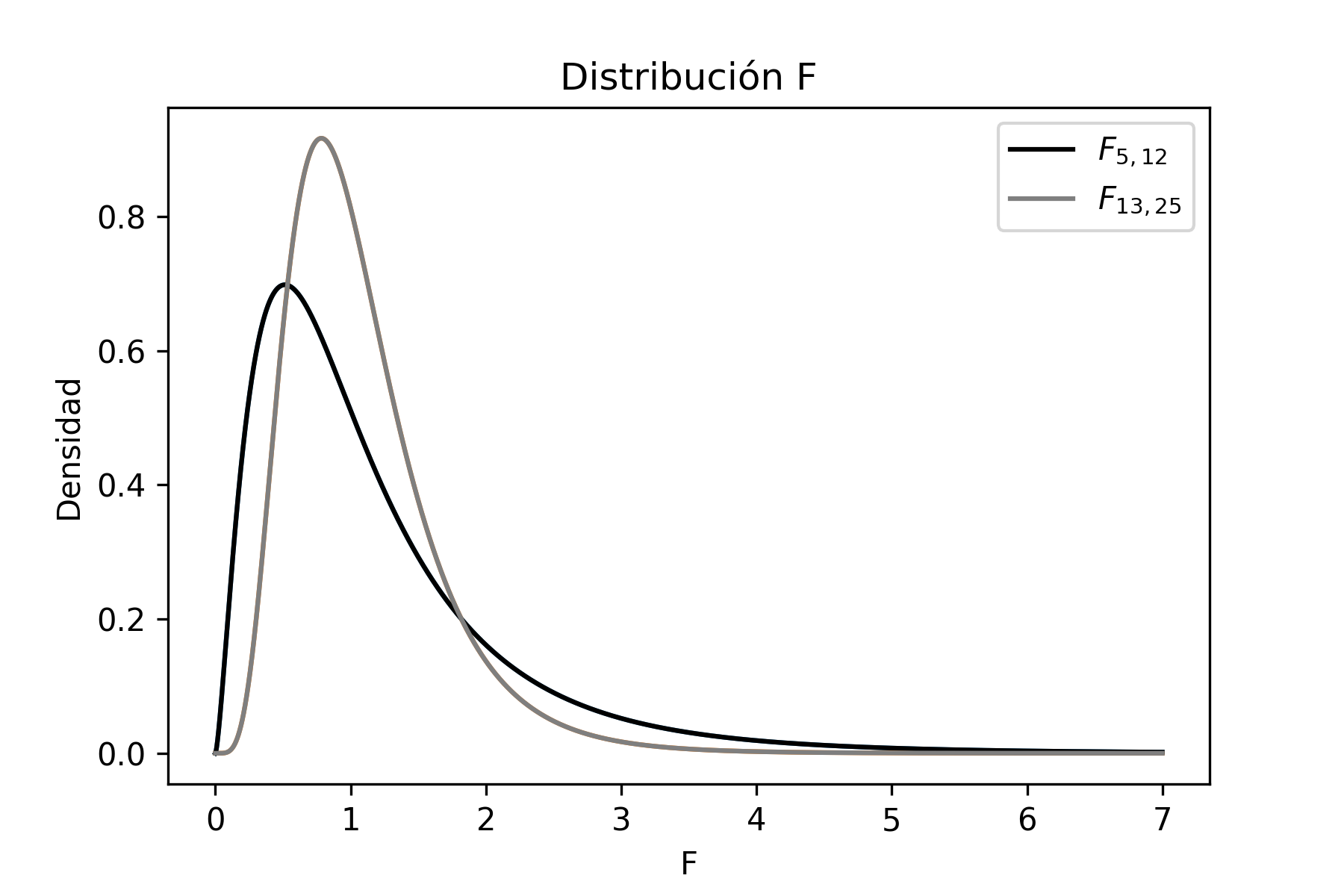
El código de Python que genera el gráfico anterior es el que sigue. Cabe destacar que las librerías necesarias para este script son las mismas que fueron utilizadas anteriormente.
# Graficando F
dfn = 5 # grados de libertad del numerador de la primera funcion
dfd = 12 # grados de libertad del denominador de la primera funcion
dfn2 = 13 # grados de libertad del numerador de la segunda funcion
dfd2 = 25 # grados de libertad del denominador de la segunda funcion
f = stats.f(dfn,dfd)
f2 = stats.f(dfn2,dfd2)
x = np.linspace(f.ppf(0.01),
f.ppf(0.99), 100)
x = np.arange(0, 7., 0.001)
#Funcion de Densidad
fp = f.pdf(x)
fp2 = f2.pdf(x)
plt.plot(x, fp)
plt.plot(x, fp2)
plt.title('Distribucion F')
plt.ylabel('Densidad')
plt.xlabel('F')
plt.plot(x, fp,label=r'$F_{5,12}$', color='black')
plt.plot(x, fp2,label=r'$F_{13,25}$',color='tab:gray')
plt.legend()
plt.show()Una transformación de la distribución \(F\) que suele ser de gran utilidad es la siguiente:
\[\begin{aligned} F^{\alpha}_{n_{1},n_{2}}=\frac{1}{F^{1-\alpha}_{n_{2},n_{1}}} \end{aligned}\]
Si se calcula la esperanza y la varianza para la distribución \(F\), se obtienen los siguientes resultados:
\[\begin{aligned} E(F)\!=\; & \frac{n_{2}-1}{(n_{2}-1)-2} \nonumber \\ V(F)\!=\; & \frac{2(n_{2}-1)^{2}\left[(n_{1}-1)+(n_{2}-1)-2\right]}{(n_{1}-1)[(n_{2}-1)-2]^{2}[(n_{2}-1)-4]} \end{aligned}\]
Distribución t-Student
Sean \(Z\) y \(U\) dos variables aleatorias donde:
\[\begin{aligned} Z&\sim & N(0,1) \nonumber \\ U &\sim & \chi^{2}_{n-1} \end{aligned}\]
Entonces la distribución \(t\) con \(n-1\) grados de libertad, se define como:
\[\begin{aligned} \label{est_t0} t_{n-1}=\frac{Z}{\sqrt{\frac{U}{n-1}}} \end{aligned}\]
Por el TCL sabemos:
\[\begin{aligned} Z\!=\; & \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \end{aligned}\]
Además, tenemos que:
\[\begin{aligned} U\!=\; & \frac{(n-1)S^{2}}{\sigma^{2}} \end{aligned}\]
Entonces, reemplazando en [est_t0]:
\[\begin{aligned} t_{n-1}\!=\; & \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{(n-1)S^{2}/\sigma^{2}}{n-1}}} \nonumber \end{aligned}\] \[\label{estadistico_t} {t_{n-1} =\frac{\overline{X}-\mu}{S/\sqrt{n}}}\]
Esta distribución es simétrica, con media cero y con menor kurtosis que la normal. Cuando la cantidad de grados de libertad tiende a infinito, la distribución \(t\) tiende a \(Z\), es decir a la normal estándar. O sea
\[\begin{aligned} \lim_{n\rightarrow \infty}t_{n-1}=Z \end{aligned}\]
La esperanza y la varianza de la distribución \(t\)-Student son:
\[\begin{aligned} E(t)\!=\; & 0 \nonumber \\ V(t)\!=\; & \frac{n-1}{(n-1)-2} \end{aligned}\]
La forma gráfica de la distribución t-Student se muestra en la siguiente figura junto a la distribución normal estándar.
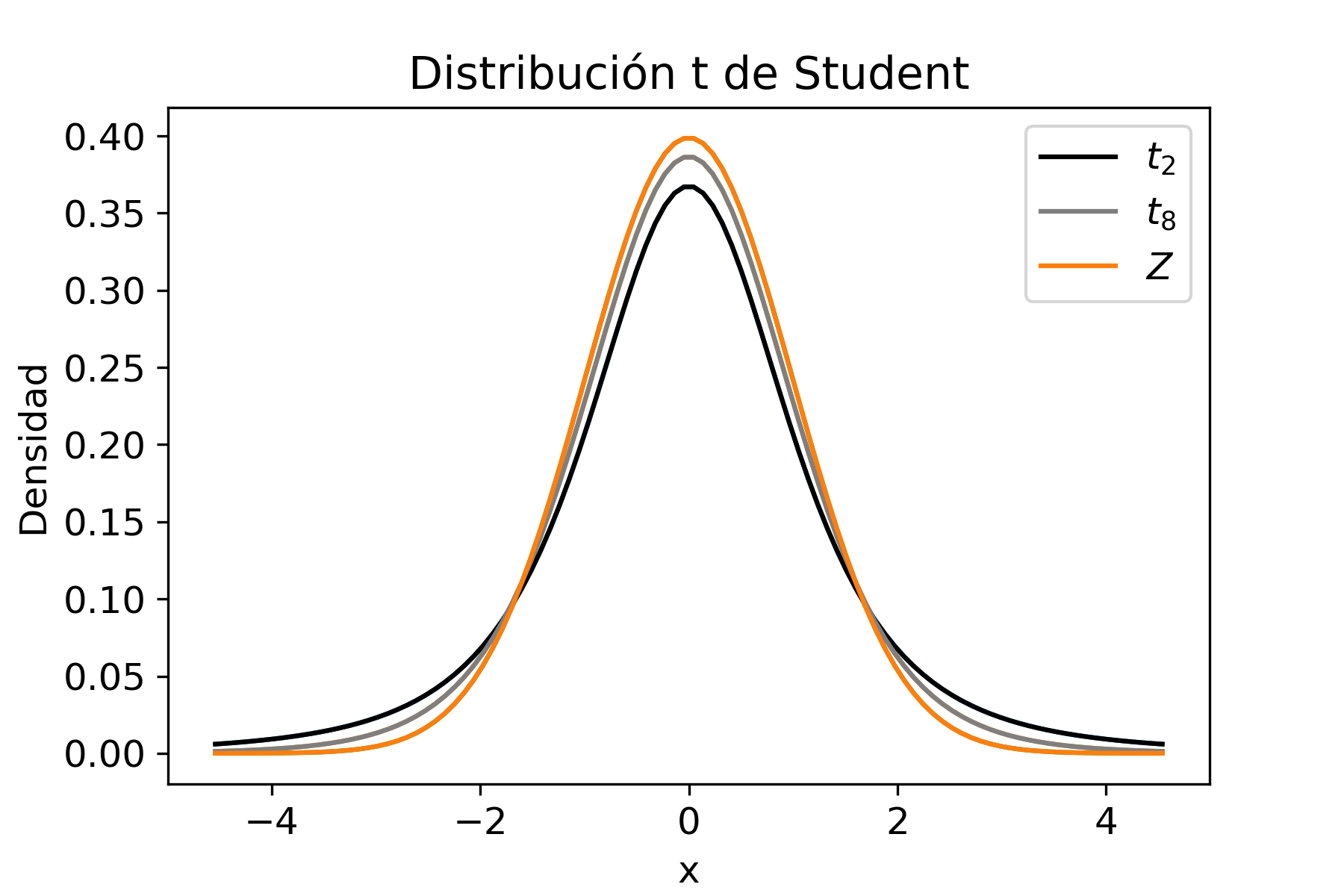
El script en Python para generar el gráfico anterior, que compara la distribución \(t\) con la normal estándar es presentado a continuación:
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from scipy.stats import norm
import scipy.stats as st
mu, sigma = 0, 1 # media y desvio estandar
normal = stats.norm(mu, sigma)
# Graficando t de Student
df = 3 # grados de libertad de la primera distribucion
df2 = 8 # grados de libertad de la segunda distribucion
t = stats.t(df)
t2 = stats.t(df2)
x = np.linspace(t.ppf(0.01),
t.ppf(0.99), 100)
fp = t.pdf(x)
fp2 = t2.pdf(x)
fp3 = normal.pdf(x)
plt.rcParams["font.size"] = "14"
plt.plot(x, fp)
plt.plot(x, fp2)
plt.plot(x, fp3)
plt.plot(x, fp,label=r'$t_{2}$',color='black')
plt.plot(x, fp2,label=r'$t_{8}$', color='tab:gray')
plt.plot(x, fp3,label=r'$Z$', color='tab:orange')
plt.title('Distribucion t de Student')
plt.ylabel('Densidad')
plt.xlabel('x')
plt.legend()
plt.show()Estimadores y sus Propiedades
Definición 1.1. Un estimador \(\hat{\theta}\) es una medida, con una forma funcional particular, que se usa para estimar el parámetro de la población \(\theta\).
Dado que, para cada parámetro poblacional, pueden existir más de un estimador, debemos poder efectuar comparaciones entre ellos para identificar el mejor. Es por ello que existen criterios para evaluar la calidad de los estimadores, que nos indican cuál es el adecuado para el parámetro considerado. Los principales criterios o propiedades son los siguientes:
Insesgado: Se denomina sesgo de un estimador a la diferencia entre la esperanza del estimador y el verdadero valor del parámetro a estimar. Es deseable que un estimador sea insesgado o centrado, es decir, que su sesgo sea nulo por ser su esperanza igual al parámetro que se desea estimar. Matemáticamente:
\[\begin{aligned} E(\hat{\theta})=\theta \end{aligned}\]
Eficiencia: Diremos que un estimador es más eficiente o más preciso que otro estimador, si la varianza del primero es menor que la del segundo3. La eficiencia nos indica el tamaño del error estándar del estadístico. Supongamos que tenemos dos estimadores \(\hat{\theta}_{1}\) y \(\hat{\theta}_{2}\) del parámetro poblacional \(\theta\), entonces el estimador \(\hat{\theta}_{1}\) será más eficiente que \(\hat{\theta}_{2}\) si se cumple que:
\[\begin{aligned} V(\hat{\theta}_{1})<V(\hat{\theta}_{2}) \end{aligned}\]
Consistencia: Si no es posible emplear estimadores de mínima varianza, el requisito mínimo deseable para un estimador es que, a medida que el tamaño de la muestra crece, el valor del estimador tienda al valor del parámetro, propiedad que se denomina consistencia. Es decir:
\[\begin{aligned} E(\hat{\theta}) \rightarrow \theta \quad \text{cuando} \quad n \rightarrow \infty \end{aligned}\]
Robustez: Un estimador \(\hat{\theta}\) de un cierto parámetro de la población \(\theta\) se dice que es robusto si la vulneración de los supuestos de partida en los que se basa la estimación (generalmente, atribuir a la población un determinado tipo de función de distribución que, en realidad, no es la correcta), no altera de manera significativa los resultados que el estimador proporciona.
Suficiencia: Se dice que un estimador es suficiente cuando resume toda la información relevante contenida en la muestra, de forma que ningún otro estimador pueda proporcionar información adicional sobre el parámetro desconocido de la población.
Problema Resuelto 1.2. Sean \(X_{1}\), \(X_{2}\) y \(X_{3}\) los valores de gasto familiar en supermercado de una muestra de tamaño 3, tomada de una localidad con gasto en supermercado promedio \(\mu\) y varianza \(\sigma^{2}\). Si definimos los siguientes estimadores para la media poblacional:
\(\overline{X}=k/3X_{1}+k/3X_{2}+k/3X_{3}\)
\(\overline{X}=k/4X_{1}+2k/4X_{2}+k/4X_{3}+1\)
\(\overline{X}=k/5X_{1}+2k/5X_{2}+2k/5X_{3}+2\)
donde \(k\in \mathrm{R}>0\).
Indique cuál de los estimadores es más eficiente y tiene menor sesgo.
Solución
Calculemos primero la esperanza para el estimador I).
\[\begin{aligned} E(\overline{X})\!=\; & E(k/3\cdot X_{1}+k/3\cdot X_{2}+k/3\cdot X_{3}) \nonumber \\ \!=\; & E(k/3\cdot X_{1})+E(k/3\cdot X_{2})+E(k/3\cdot X_{3}) \nonumber \\ \!=\; & k/3E(X_{1})+k/3E(X_{2})+k/3E(X_{3}) \nonumber \\ \!=\; & k/3\mu+k/3\mu+k/3\mu \nonumber \\ \!=\; & k \cdot \mu \end{aligned}\]
Operando de forma similar, se llega a la esperanza de los estimadores II) y III):
\[\begin{aligned} E(\overline{X})\!=\; & E(k/4\cdot X_{1}+2k/4\cdot X_{2}+k/4\cdot X_{3}+1) \nonumber \\ \!=\; & k \cdot \mu+1 \nonumber \\ E(\overline{X})\!=\; & E(k/5\cdot X_{1}+2k/5\cdot X_{2}+2k/5\cdot X_{3}+2) \nonumber \\ \!=\; & k \cdot \mu+2 \nonumber \end{aligned}\]
Los tres estimadores son sesgados, pero el que tiene el menor sesgo es el I) dado que estamos hablando de gasto en supermercado y la esperanza de esa variable es positiva y \(k\in \mathrm{R}>0\).
Ahora queda por ver cuál de los estimadores es más eficiente. Calculemos la varianza del primer caso.
\[\begin{aligned} V(\overline{X})\!=\; & V(k/3\cdot X_{1}+k/3\cdot X_{2}+k/3\cdot X_{3}) \nonumber \\ \!=\; & V(k/3\cdot X_{1})+V(k/3\cdot X_{2})+V(k/3\cdot X_{3}) \nonumber \\ \!=\; & (k/3)^{2}V(X_{1})+(k/3)^{2}V(X_{2})+(k/3)^{2}V(X_{3}) \nonumber \\ \!=\; & k^{2}/9\sigma^{2}+k^{2}/9\sigma^{2}+k^{2}/9\sigma^{2}\nonumber \\ \!=\; & k^{2}/3\sigma^{2} \end{aligned}\]
Operando para los otros dos estimadores, teniendo en cuenta que \(V(c)=0\) siendo \(c\) una constante, se obtienen los siguientes resultados:
\(V(\overline{X})=6k^{2}/16 \cdot \sigma^{2}\)
\(V(\overline{X})=9k^{2}/25 \cdot \sigma^{2}\)
Como conclusión, el estimador más eficiente es el I), pues tiene la varianza más pequeña.
Estimador de la varianza poblacional
Supongamos que construimos un estimador \(\widehat{\theta}\) de la varianza poblacional, como la suma de los desvíos respecto a la media muestral elevados al cuadrado, divida por el tamaño de la muestra \(n\). En otras palabras:
\[\begin{aligned} \widehat{\theta}\!=\; & \frac{\sum_{i=1}^{n}{(X_{i}-\overline{X})^{2}}} {n} \end{aligned}\]
Operando matemáticamente sobre el estimador \(\theta\), tenemos:
\[\begin{aligned} \widehat{\theta}\!=\; & \frac{\sum_{i=1}^{n}{(X_{i}-\overline{X})^{2}}} {n} \\ \!=\; & \frac{\sum_{i=1}^{n}{(X_{i}^{2}-2X_{i}\overline{X}+\overline{X}^{2}})} {n} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{X_{i}^{2}}-2\sum_{i=1}^{n}{X_{i}\overline{X}}+\sum_{i=1}^{n}{\overline{X}^{2}}} {n} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{X_{i}^{2}}-2n\overline{X}\overline{X}+n\overline{X}^{2}} {n} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{X_{i}^{2}}-n\overline{X}^{2}} {n} \end{aligned}\]
Tomando esperanza:
\[\begin{aligned} \label{s2} E(\widehat{\theta})\!=\; & E \Big(\frac{\sum_{i=1}^{n}{X_{i}^{2}}-n\overline{X}^{2}} {n}\Big) \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{E(X_{i}^{2})}}{n}-\frac{nE(\overline{X}^{2})}{n} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{E(X_{i}^{2})}}{n}-E(\overline{X}^{2}) \end{aligned}\]
Sabiendo que:
\[\begin{aligned} E(\overline{X})\!=\; & \mu \nonumber \\ V(\overline{X})\!=\; & \sigma^{2}/n \nonumber \\ E(X_{i})\!=\; & \mu \nonumber \\ V(X_{i})\!=\; & \sigma^{2} \end{aligned}\] y que:
\[\begin{aligned} \label{var_esp} V(X)\!=\; & E(X^{2})-(E(X))^{2} \end{aligned}\] por lo que:
\[\begin{aligned} \label{res1} E(X_{i}^{2})\!=\; & V(X_{i})+(E(X_{i}))^{2} \nonumber \\ \!=\; & \sigma^{2}+\mu^{2} \end{aligned}\]
Por otro lado, aplicando [var_esp] a la \(\overline{X}\), y despejando \(E(\overline{X}^{2})\):
\[\begin{aligned} \label{res2} E(\overline{X}^{2})\!=\; & V(\overline{X})+(E(\overline{X}))^{2} \nonumber \\ \!=\; & \sigma^{2}/n+\mu^{2} \end{aligned}\] y llevando los resultados de [res1] y [res2] a la ecuación ([s2]), tenemos que:
\[\begin{aligned} E(\widehat{\theta})\!=\; & \frac{\sum_{i=1}^{n}{E(X_{i}^{2})}}{n}-E(\overline{X}^{2}) \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{(\sigma^{2}+\mu^{2})}}{n}-(\sigma^{2}/n+\mu^{2}) \nonumber \\ \!=\; & \sigma^{2}+\mu^{2}-\sigma^{2}/n-\mu^{2} \nonumber \\ \!=\; & \frac{n-1}{n} \sigma^{2} \end{aligned}\]
Así se llega a la conclusión que, para obtener un estimador insesgado de la varianza poblacional, hay que multiplicar al estimador \(\widehat{\theta}\) por \(n/(n-1)\), es decir:
\[\begin{aligned} \label{varianza_muestral_ec} \widehat{\theta} \cdot \frac{n}{n-1}\!=\; & \frac{\sum_{i=1}^{n}{(X_{i}-\overline{X})^{2}}} {n} \cdot \frac{n}{n-1} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{(X_{i}-\overline{X})^{2}}} {n-1} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{X^{2}_{i}}-n\overline{X}^{2}} {n-1} = S^{2} \end{aligned}\]
\(S^{2}\) es entonces, el estimador insesgado de la varianza poblacional.
Estimación por Máxima Versosimilitud
Supongamos que tenemos una muestra \(X_{1}, X_{2}, \cdots, X_{n}\) de \(n\) observaciones independientes e idénticamente distribuidas, extraídas en forma aleatoria de una distribución desconocida con función de densidad (o función de probabilidad) \(f_{0}(\cdot)\). Si se sabe que \(f_{0}\) pertenece a una familia de distribuciones conocidas, el método de máxima verosimilitud consiste en seleccionar como valor estimado del parámetro de la función \(f_{0}\), aquél que maximiza la probabilidad de una muestra (a posteriori de haberla extraído), con respecto a todos los valores posibles del parámetro. En otras palabras, maximiza la probabilidad de presentación conjunta de todas las observaciones de la muestra.
Problema Resuelto 1.3. Calcular los estimadores máximo verosímiles de los parámetros \(\mu\) y \(\sigma^{2}\) de la función de distribución normal.
Solución
La función de distribución individual de una variable normal es:
\[\begin{aligned} f(\mu,\sigma^{2},X_{i})=\frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{1}{2}\frac{(X_{i}-\mu)^{2}}{\sigma^{2}}} \end{aligned}\]
Planteando la función de verosimilitud para una muestra aleatoria de tamaño \(n\)4, tenemos:
\[\begin{aligned} L(\mu,\sigma^{2},X_{i})\!=\; & f(X_{1},X_{2},...,X_{n},\mu,\sigma^{2}) \nonumber \\ \!=\; & \prod_{i=1}^{n}{f(X_{i},\mu,\sigma^{2})} \nonumber \\ \!=\; & \prod_{i=1}^{n}{\frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{1}{2}\frac{(X_{i}-\mu)^{2}}{\sigma^{2}}}} \nonumber \\ \!=\; & \bigg(\frac{1}{\sqrt{2\pi \sigma^{2}}}\bigg)^{n}e^{-\frac{1}{2}\frac{\sum_{i=1}^{n}{(X_{i}-\mu)^{2}}}{\sigma^{2}}} \end{aligned}\]
Ahora tomamos logaritmo a la función de verosimilitud, ya que es una transformación monótona que simplifica los cálculos, y operamos teniendo en cuenta las propiedades del logaritmo:
\[\begin{aligned} \ln{L(\mu,\sigma^{2},X_{i})}\!=\; & \ln{\bigg(\bigg(\frac{1}{\sqrt{2\pi \sigma^{2}}}\bigg)^{n}e^{-\frac{1}{2}\frac{\sum_{i=1}^{n}{(X_{i}-\mu)^{2}}}{\sigma^{2}}}\bigg)} \nonumber \\ \!=\; & -\frac{n}{2 } \ln{(2\pi \sigma^{2})}-\frac{1}{2}\frac{\sum_{i=1}^{n}{(X_{i}-\mu)^{2}}}{\sigma^{2}} \end{aligned}\]
En esta función debemos hallar los valores de los parámetros que la maximizan. Para ello hay que plantear las condiciones de primer orden respecto a \(\mu\) y a \(\sigma^{2}\), es decir:
\[\begin{aligned} \frac{\partial \ln{L(\mu,\sigma^{2},X_{i})}}{\partial \mu}\!=\; & -\frac{1}{2}\frac{2}{\sigma^{2}}\sum_{i=1}^{n}{(X_{i}-\mu)}(-1) \nonumber \\ \frac{\partial \ln{L(\mu,\sigma^{2},X_{i})}}{\partial \sigma^{2}}\!=\; & -\frac{n}{2} \frac{2\pi}{2\pi \sigma^{2}}-\frac{1}{2} \sum_{i=1}^{n}{(X_{i}-\mu)^{2}} (\sigma^{2})^{-2} \end{aligned}\]
Igualando la primer condición de primer orden a cero y despejando \(\mu\) obtenemos:
\[\begin{aligned} \frac{1}{\widehat{\sigma}^{2}}\sum_{i=1}^{n}{(X_{i}-\overline{X})} \!=\; & 0 \nonumber \\ \sum_{i=1}^{n}{(X_{i}-\overline{X})}\!=\; & 0 \nonumber \\ \overline{X}\!=\; & \frac{\sum_{i=1}^{n}{X_{i}}}{n} \end{aligned}\]
Si se iguala a cero la segunda condición de primer orden y se despeja \(\widehat{\sigma}^{2}\), tenemos
\[\begin{aligned} -n+\frac{\sum_{i=1}^{n}{(X_{i}-\overline{X})^{2}}}{ \widehat{\sigma}^{2}}\!=\; & 0 \nonumber \\ \widehat{\sigma}^{2}\!=\; & \frac{\sum_{i=1}^{n}{(X_{i}- \overline{X})^{2}}}{ n} \end{aligned}\]
Como vemos, el estimador máximo verosímil de la varianza es un estimador sesgado ya que utiliza los desvíos respecto a la media muestral. Por eso es que debe ser corregido para que desaparezca el sesgo, dividiendo por \(n-1\) en lugar de por \(n\) (ver [varianza_muestral_ec]).
Problema Resuelto 1.4. Una empresa de emergencias cree que la cantidad de llamadas diarias de casos graves que ingresan al call center, sigue un modelo de Poisson. Contando con una muestra de 30 días en las que se produjeron 102 llamadas de emergencias graves al call center, se desea obtener la estimación máximo verosímil del promedio de llamadas graves, suponiendo un modelo de Poisson.
Solución
La distribución de Poisson viene dada por la siguiente función de cuantía:
\[\begin{aligned} f(X_{i},\lambda)=\frac{e^{-\lambda} \lambda^{X_{i}}}{X_{i}!} \end{aligned}\]
Calculemos la función de verosimilitud.
\[\begin{aligned} L(\lambda) \!=\; & f(X_{1},X_{2},...,X_{n},\lambda) \nonumber \\ \!=\; & \prod_{i=1}^{n}\frac{e^{-\lambda} \lambda^{X_{i}}}{X_{i}!} \nonumber \\ \!=\; & \frac{(e^{-\lambda})^{n} \lambda^{\sum_{i=1}^{n}X_{i}}}{\prod_{i=1}^{n}X_{i}!} \end{aligned}\]
Tomando logaritmo a la función \(L\)
\[\begin{aligned} \ln{L(\lambda)}\!=\; & \ln{\frac{(e^{-\lambda})^{n} \lambda^{\sum_{i=1}^{n}X_{i}}}{\prod_{i=1}^{n}X_{i}!}} \nonumber \\ \!=\; & \ln{(e^{-\lambda}})^{n}+\ln{\lambda^{\sum_{i=1}^{n}X_{i}}}-\ln{\prod_{i=1}^{n}X_{i}!} \nonumber \\ \!=\; & -\lambda n + \sum_{i=1}^{n}X_{i} \ln{\lambda} -\ln{\prod_{i=1}^{n}X_{i}!} \end{aligned}\]
Planteando la condición de primer orden
\[\begin{aligned} \frac{\partial \ln{L(\lambda)}}{\partial \lambda}\!=\; & -n +\sum_{i=1}^{n}X_{i} \frac{1}{\lambda} \end{aligned}\]
Igualando a cero y despejando \(\widehat{\lambda}\) tenemos:
\[\begin{aligned} -n +\sum_{i=1}^{n}X_{i} \frac{1}{\widehat{\lambda}}\!=\; & 0 \nonumber \\ \widehat{\lambda}\!=\; & \frac{\sum_{i=1}^{n}X_{i}}{n} \end{aligned}\]
Teniendo en cuenta que \(n=30\) y que se produjeron en total 102 siniestros, el valor estimado de \(\lambda\) es:
\[\begin{aligned} \widehat{\lambda}\!=\; & \frac{\sum_{i=1}^{n}x_{i}}{n}=\frac{102}{30}=3.4 \quad \text{llamadas de casos graves por día} \end{aligned}\]
Hay que recordar que, en esta distribución, una vez que se tiene la media, no es necesario calcular la varianza porque es igual a la media.
Problema Resuelto 1.5. Dada la función de verosimilitud conjunta5:
\[\begin{aligned} \label{act5_1} L(P)=C_{n}^{\sum X_{i}}P^{\sum X_{i}}(1-P)^{n-\sum X_{i}} \end{aligned}\] determine el estimador máximo verosímil de \(P\), es decir, de la proporción poblacional de éxitos.
Solución
Tomando logaritmo a la función de la ecuación [act5_1], tenemos:
\[\begin{aligned} \label{act5_2} \ln{L(P))}\!=\; & \ln{C_{n}^{\sum X_{i}}P^{\sum X_{i}}(1-P)^{n-\sum X_{i}}} \nonumber \\ \!=\; & \ln{C_{n}^{\sum X_{i}}}+\ln{P^{\sum X_{i}}}+(n-\sum X_{i})\ln{(1-P)} \end{aligned}\]
Derivando respecto de \(P\) la ecuación [act5_2] para calcular la condición de primer orden, nos queda
\[\begin{aligned} \frac{\partial \ln{L(P))}}{\partial P}\!=\; & \frac{\sum X_{i}}{P}-\frac{n-\sum X_{i}}{1-P} \end{aligned}\]
Igualando a cero y despejando \(\widehat{P}\) llegamos a:
\[\begin{aligned} \frac{\sum X_{i}}{\widehat{P}}-\frac{n-\sum X_{i}}{1-\widehat{P}}\!=\; & 0 \nonumber \\ \frac{\widehat{P}}{\sum X_{i}}\!=\; & \frac{1-\widehat{P}}{n-\sum X_{i}} \nonumber \\ \widehat{P}({n-\sum X_{i}})\!=\; & ({1-\widehat{P}}){\sum X_{i}} \nonumber \\ \widehat{P}\!=\; & \frac{\sum X_{i}}{n} \end{aligned}\]
Lo que nos dice que el estimador máximo verosímil de la proporción poblacional, es la proporción muestral.
Intervalos de Confianza
Cuando queremos hacer inferencia sobre algún parámetro poblacional, construimos un estimador que sea el adecuado para realizar la conjetura acerca del valor exacto del mismo. Sin embargo, esa estimación puntual del parámetro no da ningún tipo de información sobre el posible grado de “error” que podemos estar cometiendo, y es por ello que surge la noción de intervalo de confianza. Entonces, teniendo en cuenta el estimador, podemos construir un intervalo con el que vamos a decir que tenemos una cierta confianza de que el verdadero parámetro poblacional estará contenido en dicho intervalo. En este capítulo, y teniendo en cuenta las aplicaciones del TCL, vamos a desarrollar intervalos para los parámetros poblacionales media, proporción y varianza.
Definición 2.1 (Estimación por Intervalos). Una estimación de intervalo describe un rango de valores dentro del cual es posible, con un cierto nivel de confianza, que esté contenido el verdadero valor del parámetro poblacional que se desea averiguar.
El nivel de confianza, que se denota como \((1-\alpha)\), es la probabilidad máxima con la que podríamos asegurar que el verdadero valor del parámetro poblacional se encuentra dentro de nuestro intervalo estimado.
El procedimiento consiste primero en realizar la estimación puntual del parámetro poblacional, luego calcular el error probable de esa estimación y, por último, determinar la confianza de que el intervalo contenga dicho valor del parámetro.
Intervalos para la Media Poblacional
Intervalos para la Media de una Población
Se distinguirán dos situaciones. Por un lado, cuando conocemos el valor de la varianza poblacional y, por el otro, cuando ese valor es desconocido.
Varianza conocida
Sea una variable aleatoria \(X\) con media \(\mu\) y varianza \(\sigma^{2}\), entonces por el TCL, cuando \(n\) es grande, tenemos que:
\[\begin{aligned} \label{z} \overline{X} & \sim & N(\mu,\sigma^{2}/n) \nonumber \\ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} & \sim & N(0,1) \end{aligned}\]
Ahora bien, podemos calcular la probabilidad acumulada entre dos puntos (que denotaremos como \(Z_{\alpha/2}\) y \(Z_{1-\alpha/2}\)) tal que dicha probabilidad sea igual a \(1-\alpha\), entonces:
\[\begin{aligned} P(Z_{\alpha/2}\leq Z \leq Z_{1-\alpha/2})\!=\; & 1-\alpha \end{aligned}\]
Reemplazando \(Z\) por el estadístico [z], tenemos:
\[\begin{aligned} \label{ic_z} P\bigg(Z_{\alpha/2}\leq \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq Z_{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando \(\mu\) de la desigualdad contenida en el paréntesis de la ecuación anterior, obtenemos:
\[\begin{aligned} P\bigg(Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \overline{X}-\mu \leq Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg(-\overline{X} + Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \leq -\mu\leq-\overline{X} + Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \end{aligned}\] \[\label{ic_media} {P\bigg(\overline{X} - Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} - Z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\bigg)=1-\alpha}\]
En la última igualdad, la expresión contenida en el paréntesis de la probabilidad nos determina los límites inferior y superior del intervalo para la media, que llamaremos intervalo de confianza, . Con lo cual se puede afirmar que existe una probabilidad de \(1-\alpha\) que el intervalo de confianza contenga el verdadero valor de la media poblacional.
El proceso para llegar a esa expresión es la que utilizaremos en lo sucesivo para construir los intervalos de confianza de los parámetros poblacionales, con el cambio que corresponda, según sea la distribución asociada que tenga el estimador utilizado en el análisis.
Problema Resuelto 2.1. Una empresa que vende agroquímicos para los cultivos quiere saber la cantidad mensual, en promedio por cliente, que vende de un agroquímico específico para el cultivo de soja. Para ello, toma una muestra al azar de 50 clientes y encuentra que, en promedio, vendió \(15.03\) dosis. Si sabe por estudios anteriores que la población se distribuye aproximadamente normal con una desviación estándar de 3 dosis, se pide:
Hallar un intervalo de confianza del 95% para la media de la venta mensual de dicho agroquímico
Si luego se conociera que la media poblacional es de 14 dosis, ¿qué pudo haber pasado?
Hallar un intervalo de confianza del 99%. Explicar la diferencia con el obtenido en el primer punto
Solución
Para calcular el intervalo de confianza del 95% para la media, y debido a que se trata de una población aproximadamente normal6, entonces podemos afirmar que:
\[\begin{aligned} \overline{x} - Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq &\mu& \leq \overline{x} - Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \nonumber \\ 15.03 - 1.96 \frac{3}{\sqrt{50}} \leq & \mu & \leq 15.03 - (-1.96) \frac{3}{\sqrt{50}} \nonumber \\ 14.19 \leq & \mu & \leq 15.86 \end{aligned}\]
Como conclusión, podemos decir que el intervalo construido con la muestra extraída contendrá, con un 95% de confianza, el verdadero valor del parámetro poblacional (en este caso, la media). Hay que destacar que extraemos una única muestra, que proviene del universo que contiene todas las muestras posibles de tamaño \(n\) (en este caso \(n=50\)), que se pueden formar con los elementos de la población con dispersión \(\sigma^{2}\) (en este caso \(\sigma^{2}=9\)). De ese universo que, en general, es muy grande podría haber sido seleccionada cualquier otra muestra, en lugar de la que extrajimos. En ese caso hubiésemos construido un intervalo de confianza diferente. Es importante entonces conocer, de antemano, que en ese gran universo de muestras posibles, el 95% de ellas nos conducen a construir un intervalo de confianza que contiene el verdadero valor del parámetro poblacional y que el 5% restante nos llevan, en cambio, a plantear un intervalo que no contiene el verdadero valor del parámetro poblacional. En otros términos, en promedio, de cada cien muestras posibles, 95 nos conducirán a una inferencia correcta acerca del parámetro poblacional, mientras las otras 5 nos llevarán a una predicción errónea. Esto es precisamente el significado del nivel de confianza.
Ahora bien, si luego se conoce que la media poblacional es 14 dosis, pueden haber sucedido básicamente dos cosas: o que tuvimos “mala suerte” y sacamos una muestra aleatoria (que tiene sólo el 5% de probabilidad de presentarse), cuyo intervalo no contiene la media poblacional y, por lo tanto, nos condujo a realizar una inferencia incorrecta; o bien que hay un problema de muestreo, como podría ser que la selección no fue aleatoria, que la medición de la cantidad de dosis de agroquímicos no fue correctamente realizada, etc.
Gráficamente, la situación hubiese sido:
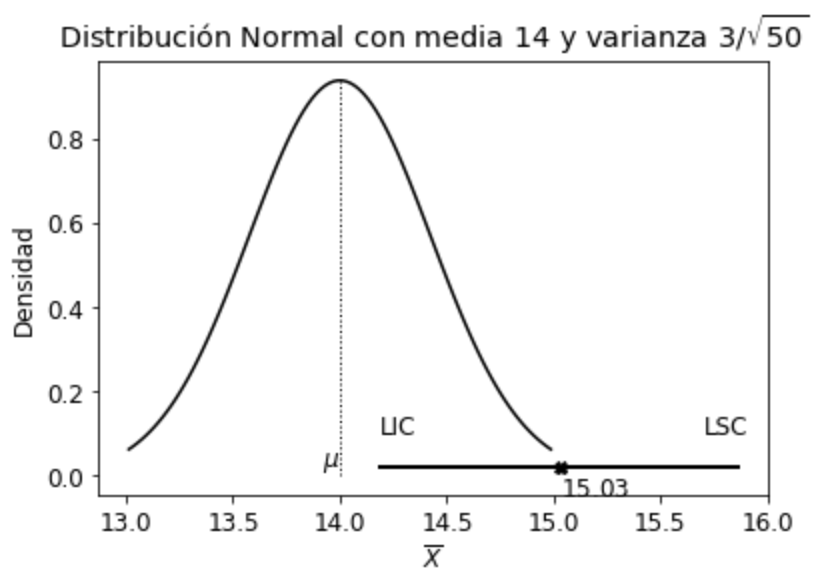
Se puede observar claramente que el intervalo de confianza no incluye al verdadero valor del parámetro poblacional (\(\mu=14\)).
Si consideramos un nivel de confianza del 99%, el intervalo es:
\[\begin{aligned} \overline{x} - Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq &\mu& \leq \overline{x} - Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \nonumber \\ 15.03 - 2.58 \frac{3}{\sqrt{50}} \leq & \mu & \leq 15.03 - (-2.58) \frac{3}{\sqrt{50}} \nonumber \\ 13.93 \leq & \mu & \leq 16.12 \end{aligned}\]
Como podemos ver, el intervalo de confianza es más amplio que el anterior, es decir perdemos precisión para poder tener mayor confianza. En este último caso, si la media poblacional hubiese sido igual a 14, entonces el intervalo hubiese contenido al valor del parámetro poblacional a un nivel de confianza del 99%.
Sólo es posible aumentar la precisión y el nivel de confianza simultáneamente tomando una muestra de mayor tamaño.
Para calcular el intervalo de confianza con Python usamos el siguiente código:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Nivel de confianza
nivel_conf=0.95
# Varianza poblacional
var=3**2
# Datos muestrales
data=[13.68,13.57,10.26,12.4,16.99,13.98,16.13,19.23,17.76,16.1,
16.79,11.54,17.62,14.17,17.02,13.12,13.97,16.69,13.62,15.58,
12.4,14.92,16.74,15.39,13.42,15.67,15.25,15.35,15.35,14.52,
15.42,16.47,12.91,16.17,13.65,14.67,13.94,15.03,16.01,15.75,
16.28,16.22,15.77,13.95,16.24,14.63,12.36,15.08,17.19,14.52]
def ic(data,var,nivel_conf):
n = len(data)
z = norm.ppf(nivel_conf+(1-nivel_conf)/2)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
sigma=np.sqrt(var)
lim_inf=data_mean-z*sigma/n**0.5
lim_sup=data_mean+z*sigma/n**0.5
return lim_inf,lim_sup,z,data_mean,data_sd,n
lim_inf,lim_sup,z,data_mean,data_sd,n = ic(data,var,nivel_conf)
print("Media Muestral =",data_mean)
print("S Muestral =",data_sd)
print("n muestral =",n)
print("z =", z)
print("Intervalo de confianza: ","[",lim_inf,";",lim_sup,"]")
Media Muestral = 15.0298
S Muestral = 1.7327063766706414
n muestral = 50
z = 1.959963984540054
Intervalo de confianza: [ 14.198257705390192 ; 15.861342294609807 ]Varianza desconocida
Para estimar intervalos de confianza para la media cuando la varianza poblacional es desconocida y la población es normal, se debe que usar el estadístico \(t\) (ver [estadistico_t]), es decir:
\[\begin{aligned} \frac{\overline{X}-\mu}{S/\sqrt{n}} \sim t_{n-1} \end{aligned}\]
Problema Resuelto 2.2. Una empresa dedicada a la fabricación de pilas recargables desea estimar, con un nivel de confianza del 95%, la duración media, medida en ciclos, de un tipo nuevo de pilas para iniciar una campaña publicitaria. Con ese objetivo, toma una muestra aleatoria de \(n=10\) pilas y obtiene los siguientes resultados:
| Media Muestral | 733 |
| Desviación estándar Muestral | 112 |
Suponer población normal para la duración de los ciclos de las pilas.
Solución
Por ser la varianza desconocida, la población normal y \(n\) pequeño, al intervalo de confianza para la media poblacional lo construimos con el estadístico de la distribución \(t\):
\[\begin{aligned} P(t_{n-1;\alpha/2}\leq t_{n-1} \leq t_{n-1;1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(t_{n-1;\alpha/2}\leq \frac{\overline{X}-\mu}{S/\sqrt{n}}\leq t_{n-1;1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando \(\mu\) dentro del paréntesis de la ecuación anterior, tenemos:
\[\begin{aligned} P\bigg(t_{n-1;\alpha/2} \frac{S}{\sqrt{n}} \leq \overline{X}-\mu \leq t_{n-1;1-\alpha/2} \frac{S}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg(-\overline{X} + t_{n-1;\alpha/2} \frac{S}{\sqrt{n}} \leq -\mu\leq-\overline{X} + t_{n-1;1-\alpha/2} \frac{S}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \end{aligned}\] \[{P\bigg(\overline{X} - t_{n-1;1-\alpha/2} \frac{S}{\sqrt{n}} \leq \mu \leq \overline{X} - t_{n-1;\alpha/2} \frac{S}{\sqrt{n}}\bigg)=1-\alpha}\]
Teniendo en cuenta que la media muestral es \(733\), el tamaño de muestra 10, y la desviación muestral \(112\), el intervalo que resulta es:
\[\begin{aligned} \overline{x} - t_{n-1;1-\alpha/2} \frac{s}{\sqrt{n}} \leq &\mu& \leq \overline{x} - t_{n-1;\alpha/2} \frac{s}{\sqrt{n}} \nonumber \\ 733 - 2.262 \frac{112}{\sqrt{10}} \leq & \mu & \leq 733 - (-2.262) \frac{112}{\sqrt{10}} \nonumber \\ 652.89 \leq & \mu & \leq 813.11 \end{aligned}\]
Como conclusión, podemos decir que tenemos una confianza del 95% que el verdadero valor del parámetro poblacional (\(\mu\)) estará entre \(652.89\) y \(813.11\), o sea que la duración media de las pilas, medida en ciclos, estará entre estos dos valores.
Si la población no es normal se presentan las siguientes opciones:
Con \(n\) pequeño habría que tratar de transformar la variable para que la distribución poblacional se aproxime a una normal. En numerosas ocasiones, la transformación logarítmica o raíz cuadrada suele ser óptima.
Si la muestra es lo suficientemente grande, y teniendo en cuenta que \(S\) es un estimador consistente de \(\sigma\), se puede usar el estadístico \(Z=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\)
Si la muestra es chica, y no se puede transformar la variable para que, en la población, se distribuya aproximadamente normal, se deberá recurrir a la desigualdad de Chebycheff, con la que se podrá obtener una cota máxima para la probabilidad que la media muestral difiera, en valor absoluto, respecto de la media poblacional en más de un cierto valor. Para ello es suficiente con conocer \(\sigma\), o tener una aproximación de su valor.
Intervalos para la Diferencia de Medias de dos Poblaciones
Se tienen dos poblaciones de las que se extrae una muestra de cada una de ellas. Se deben distinguir los casos según las muestras sean independientes o no, y según sus varianzas poblacionales sean conocidas o no.
Muestras independientes con varianzas conocidas
Sean dos variables aleatorias \(X_{1}\) y \(X_{2}\) que se distribuyen normalmente, entonces, por el TCL podemos escribir:
\[\begin{aligned} \overline{X}_{1} &\sim& N(\mu_{1},\sigma_{1}^{2}/n_{1}) \nonumber \\ \overline{X}_{2} &\sim& N(\mu_{2},\sigma_{2}^{2}/n_{2}) \end{aligned}\]
Restando ambas variables y estandarizando tenemos:
\[\begin{aligned} \label{iic_z2mi} \overline{X}_{1} -\overline{X}_{2} &\sim& N \bigg(\mu_{1}-\mu_{2},\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2} \bigg) \nonumber \\ \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}}} &\sim & N(0,1) \end{aligned}\]
Esto es así porque la suma (diferencia) de variables que son independientes y de distribución normal es otra variable que también se distribuye normalmente, con media igual a la suma (diferencia) de las medias y varianza igual a la suma de varianzas. El intervalo de confianza se construye utilizando este estadístico.
Problema Resuelto 2.3. Los directores de una empresa dedicada a la fabricación de dispositivos de almacenamiento digital deben decidir la implementación (o no) de un nuevo proceso que aumentaría la velocidad de acceso de los dispositivos a los datos almacenados en los mismos. Es por ello, que quieren saber si la velocidad es superior en el nuevo proceso en relación al proceso antiguo. Para ello, el departamento de calidad de la empresa tomó dos muestras de dispositivos de almacenamiento y les aplicó, a una el proceso antiguo y a la otra el nuevo proceso, obteniéndose los siguientes resultados:
| Proceso antiguo | Proceso nuevo | |
|---|---|---|
| n | 100 | 150 |
| \(\sum_{i}x_{i}\) (Mbytes/s) | 56 000 | 85 515 |
Además, se conoce que:
| Proceso antiguo | Proceso nuevo | |
|---|---|---|
| \(\sigma\) | 50 | 60 |
A partir de la construcción de un intervalo de confianza con \(1-\alpha=0.95\), ¿a qué conclusión se llega?
Solución
Teniendo en cuenta la ecuación [iic_z2mi], dado que estamos trabajando con dos muestras independientes, entonces podemos escribir:
\[\begin{aligned} P(Z_{\alpha/2}\leq Z \leq Z_{1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(Z_{\alpha/2}\leq \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}}}\leq Z_{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Operando sobre la desigualdad anterior, tenemos:
\[\begin{aligned} P\bigg(Z_{\alpha/2} \sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}} \leq (\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2}) \leq Z_{1-\alpha/2} \sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}} \bigg)=1-\alpha \nonumber \\ P\bigg(-(\overline{X}_{1} -\overline{X}_{2})+Z_{\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \leq -(\mu_{1}-\mu_{2}) \leq -(\overline{X}_{1} -\overline{X}_{2})+Z_{1-\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \bigg)=1-\alpha \nonumber \end{aligned}\] \[{P\bigg((\overline{X}_{1} -\overline{X}_{2})-Z_{1-\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \leq (\mu_{1}-\mu_{2}) \leq (\overline{X}_{1} -\overline{X}_{2})-Z_{\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \bigg)= 1-\alpha}\]
Como se observa, tenemos el intervalo de confianza para la diferencia de medias poblacionales, es decir para \((\mu_{1}-\mu_{2})\).
Teniendo en cuenta que, en este caso, las medias muestrales son iguales a:
\[\begin{aligned} \overline{x}_{1}\!=\; & \frac{\sum_{i}x_{1i}}{n_{1}}=\frac{56\,000}{100}=560 \nonumber \\ \overline{x}_{2}\!=\; & \frac{\sum_{i}x_{2i}}{n_{2}}=\frac{85\,515}{150}=570.1 \end{aligned}\] expresadas en \(Mbytes/s\), podemos calcular el intervalo de confianza como:
\[\begin{aligned} (\overline{x}_{1} -\overline{x}_{2})-Z_{1-\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \leq &(\mu_{1}-\mu_{2}) &\leq (\overline{x}_{1} -\overline{x}_{2})-Z_{\alpha/2} \sqrt{\frac{\sigma_{1}^{2}}{n_{1}} +\frac{\sigma_{2}^{2}}{n_{2}}} \nonumber \\ (560 -570.1)-1.96 \sqrt{\frac{50^{2}}{100} +\frac{60^{2}}{150}} \leq & (\mu_{1}-\mu_{2}) & \leq (560 -570.1)-(-1.96) \sqrt{\frac{50^{2}}{100} +\frac{60^{2}}{150}} \nonumber \\ -23.82 \leq & (\mu_{1}-\mu_{2}) & \leq 3.62 \nonumber \\ \end{aligned}\]
Como el valor \((\mu_{1}-\mu_{2})=0\) está incluido en el intervalo que obtuvimos, es decir, es uno de los valores que podría tomar la diferencia de medias de las poblaciones (con un nivel de confianza del 95%), entonces la conclusión es que no existen diferencias estadísticamente significativas entre las velocidades de acceso de ambos dispositivos.
Muestras independientes con varianzas desconocidas
Cuando estamos en presencia de una estimación por intervalos de confianza de una diferencia de medias con varianzas desconocidas, se debe buscar un estadístico que cumpla la condición de no contener las varianzas poblacionales. Sabiendo que una variable aleatoria con distribución \(t\) se define como:
\[\begin{aligned} \label{def_t} \frac{Z}{\sqrt{\frac{U}{n-1}}} \sim t_{n-1} \end{aligned}\] y que además la suma de dos estadísticos con distribuciones \(\chi^{2}_{n_{1}-1}\) y \(\chi^{2}_{n_{2}-1}\) nos da como resultado otra distribución \(\chi^{2}_{n_{1}+n_{2}-2}\), es decir que:
\[\begin{aligned} \label{sum_chi} \chi^{2}_{n_{1}-1} + \chi^{2}_{n_{2}-1} &\sim & \chi^{2}_{n_{1}+n_{2}-2} \nonumber \\ \frac{(n_{1}-1)S^{2}_{1}}{\sigma^{2}_{1}}+\frac{(n_{2}-1)S^{2}_{2}}{\sigma^{2}_{2}} &\sim & \chi^{2}_{n_{1}+n_{2}-2} \end{aligned}\] entonces, podemos utilizar [iic_z2mi] y [sum_chi] para reemplazar, respectivamente el numerador y el denominador en [def_t]
\[\begin{aligned} \frac{Z}{\sqrt{\frac{U}{n-1}}} &\sim & t_{n-1} \nonumber \\ \frac{\frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma^{2}_{1}/n_{1} +\sigma^{2}_{2}/n_{2}}}}{\sqrt{\frac{\frac{(n_{1}-1)S^{2}_{1}}{\sigma^{2}_{1}}+\frac{(n_{2}-1)S^{2}_{2}}{\sigma^{2}_{2}}}{n_{1}+n_{2}-2}}} &\sim & t_{n_{1}+n_{2}-2} \end{aligned}\]
Bajo el supuesto de que las varianzas poblacionales son iguales, es decir \(\sigma^{2}_{1}=\sigma^{2}_{2}=\sigma^{2}\), entonces podemos escribir la expresión anterior como:
\[\begin{aligned} \label{estadistico_t2mi} \frac{\frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma^{2}/n_{1} +\sigma^{2}/n_{2}}}}{\sqrt{\frac{\frac{(n_{1}-1)S^{2}_{1}}{\sigma^{2}}+\frac{(n_{2}-1)S^{2}_{2}}{\sigma^{2}}}{n_{1}+n_{2}-2}}} &\sim & t_{n_{1}+n_{2}-2} \nonumber \\ \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{S^{2}_{p} (\frac{1}{n_{1}}+\frac{1}{n_{2}})}} &\sim & t_{n_{1}+n_{2}-2} \end{aligned}\] que es el estadístico que se utiliza para construir el intervalo de confianza, donde \(S^{2}_{p}=\frac{(n_{1}-1)S^{2}_{1}+(n_{2}-1)S^{2}_{2}}{n_{1}+n_{2}-2}\) es la varianza de la diferencia de medias, que contiene la media ponderada de las varianzas muestrales.
Problema Resuelto 2.4. El gerente de una empresa, que posee estaciones de servicios en distintas ciudades del país, piensa que las medias de la venta diaria de combustible del tipo premium (medido en litros), de las dos principales ciudades del país, son diferentes. Para saber si esto es así, se toman muestras aleatorias de 9 casos cada una, con los siguientes resultados:
| Caso | Ciudad A | Caso | Ciudad B | |
|---|---|---|---|---|
| 1 | 270,0 | 1 | 350,0 | |
| 2 | 160,0 | 2 | 600,3 | |
| 3 | 357,4 | 3 | 424,9 | |
| 4 | 100,0 | 4 | 300,0 | |
| 5 | 283,2 | 5 | 490,3 | |
| 6 | 250,0 | 6 | 490,2 | |
| 7 | 130,0 | 7 | 404,2 | |
| 8 | 200,2 | 8 | 404,2 | |
| 9 | 154,8 | 9 | 388,8 | |
| \(\overline{X}\) | 211,7 | \(\overline{X}\) | 428,1 | |
| \(S\) | 83,97 | \(S\) | 88,45 |
Con un nivel de confianza del 99%, se pide que opine sobre lo que piensa el gerente de la empresa
Solución
Partiendo de que estamos ante la presencia de una estimación por intervalo de confianza de diferencia de medias con muestras independientes, y con las varianzas poblacionales desconocidas pero que se suponen son iguales, entonces usamos el estadístico [estadistico_t2mi]. Es decir:
\[\begin{aligned} &&P\bigg(t_{n_{1}+n_{2}-2}^{\alpha/2} \leq t \leq t_{n_{1}+n_{2}-2}^{1-\alpha/2}\bigg)=1-\alpha \nonumber \\ &&P\bigg(t_{n_{1}+n_{2}-2}^{\alpha/2}\leq \frac{(\overline{X}_{1} -\overline{X}_{2})- (\mu_{1}-\mu_{2}) }{\sqrt{S^{2}_{p} (\frac{1}{n_{1}}+\frac{1}{n_{2}})}} \leq t_{n_{1}+n_{2}-2}^{1-\alpha/2}\bigg)=1-\alpha \nonumber \\ &&P\bigg(t_{n_{1}+n_{2}-2}^{\alpha/2} \sqrt{S^{2}_{p} (\frac{1}{n_{1}}+\frac{1}{n_{2}})} \leq (\overline{X}_{1} - \overline{X}_{2})- (\mu_{1}-\mu_{2}) \leq t_{n_{1}+n_{2}-2}^{1-\alpha/2} \sqrt{S^{2}_{p} (\frac{1}{n_{1}}+\frac{1}{n_{2}})}\bigg) =1-\alpha \nonumber \\ &&P\bigg(-(\overline{X}_{1} -\overline{X}_{2})+t_{n_{1}+n_{2}-2}^{\alpha/2} S^{*}_{p} \leq -(\mu_{1}-\mu_{2}) \leq -(\overline{X}_{1} -\overline{X}_{2})+ t_{n_{1}+n_{2}-2}^{1-\alpha/2}) S^{*}_{p}\bigg) =1-\alpha \nonumber \end{aligned}\] \[{P\bigg((\overline{X}_{1} -\overline{X}_{2})-t_{n_{1}+n_{2}-2}^{1-\alpha/2} S^{*}_{p} \leq (\mu_{1}-\mu_{2}) \leq (\overline{X}_{1} -\overline{X}_{2})- t_{n_{1}+n_{2}-2}^{\alpha/2} S^{*}_{p}\bigg) =1-\alpha}\] donde \(S^{*}_{p}=\sqrt{S^{2}_{p} (\frac{1}{n_{1}}+\frac{1}{n_{2}})}\).
Teniendo en cuenta que \(t_{9+9-2}^{0.995}=2.92\), entonces podemos plantear el intervalo de confianza como:
\[\begin{aligned} (\overline{x}_{1} -\overline{x}_{2})-t_{n_{1}+n_{2}-2}^{1-\alpha/2} s^{*}_{p} \leq &(\mu_{1}-\mu_{2})& \leq (\overline{x}_{1} -\overline{x}_{2})- t_{n_{1}+n_{2}-2}^{\alpha/2} s^{*}_{p} \nonumber \\ (211.7 -428.1)-2.92 \sqrt{7\,436,6 (\frac{1}{9}+\frac{1}{9})} \leq & (\mu_{1}-\mu_{2}) & \leq (211.7 -428.1)-(- 2.92) \sqrt{7\,436,6(\frac{1}{9}+\frac{1}{9})} \nonumber \\ -410.2 \leq & (\mu_{1}-\mu_{2}) & -22.5 \nonumber \\ \end{aligned}\] donde \(S^{2}_{p}=7\,436,6\).
Conclusión: podemos decir que, dado que el intervalo de confianza no incluye el valor cero, hay evidencia estadística para afirmar que la venta de combustible premium es diferente en las dos ciudades, con lo que el gerente estaría en lo correcto.
Muestras dependientes
Cuando trabajamos con dos muestras dependientes, o sea, que tenemos fundamentos para pensar que los valores de ambas variables están relacionados, no se puede usar ninguno de los estadísticos anteriores, ya que fueron deducidos bajo el supuesto de que las variables eran independientes.
Supongamos dos variables \(X_{1}\) y \(X_{2}\) las cuales son dependientes. Se define entonces una nueva variable como la diferencia entre ambas, es decir:
\[\begin{aligned} d=X_{1}-X_{2} \end{aligned}\]
A la variable \(d\) se le puede calcular su media muestral \(\overline{d}\) y su respectiva desviación estándar muestral \(S_{d}\). Entonces, el estadístico que se usa para crear el intervalo de confianza sobre la media con muestras dependientes es:
\[\begin{aligned} \label{est_m2md} \frac{\overline{d}-\delta}{S_{d}/\sqrt{n}} \sim t_{n-1} \end{aligned}\] donde \(\delta\) es el parámetro poblacional de la diferencia de medias de ambas variables en la población y \(d\) es estimador de dicho parámetro. El estadístico [est_m2md] es el que se utiliza para confeccionar el intervalo de confianza, en este caso.
Problema Resuelto 2.5. Una empresa que se dedica a la fabricación de bicicletas, desea comparar el desgaste de dos tipos de cubiertas. Para realizar la comparación se colocan en la rueda trasera de cada una de 12 bicicletas una cubierta de un tipo y en la delantera la del otro tipo. Luego, se recorre una cierta cantidad de kilómetros preestablecidos para cada bicicleta y se registra el desgaste de cada cubierta, medido en milímetros de pérdida de espesor. En la siguiente tabla se presentan los resultados obtenidos:
| Bicicleta | Cubierta I | Cubierta II |
|---|---|---|
| 1 | 7,3 | 12,0 |
| 2 | 9,8 | 10,5 |
| 3 | 8,6 | 9,4 |
| 4 | 7,9 | 9,5 |
| 5 | 8,7 | 10,0 |
| 6 | 8,4 | 10,9 |
| 7 | 8,6 | 11,1 |
| 8 | 7,2 | 9,2 |
| 9 | 9,4 | 10,2 |
| 10 | 8,9 | 9,3 |
| 11 | 7,9 | 10,2 |
| 12 | 8,5 | 9,5 |
| \(\overline{X}\) | 8,4 | 10,2 |
| \(S\) | 0,8 | 0,9 |
¿Se puede decir que el desgaste es distinto en los diferentes tipos de cubierta? Trabajar con un nivel de confianza del 95%. Suponer que no hay diferencia en el desgaste debido a la ubicación de las cubiertas.
Solución
Como las cubiertas están instalados en una misma bicicleta, las dos muestras pueden considerarse dependientes, ya que recorren la misma distancia por idénticos trayectos y, por lo tanto, están sometidos a igual esfuerzo de desgaste. Calculando la nueva variable \(d\), tenemos:
| Bicicleta | Cubierta I | Cubierta II | \(d=I-II\) |
|---|---|---|---|
| 1 | 7,3 | 12 | -4,7 |
| 2 | 9,8 | 10,5 | -0,7 |
| 3 | 8,6 | 9,4 | -0,8 |
| 4 | 7,9 | 9,5 | -1,6 |
| 5 | 8,7 | 10 | -1,3 |
| 6 | 8,4 | 10,9 | -2,5 |
| 7 | 8,6 | 11,1 | -2,5 |
| 8 | 7,2 | 9,2 | -2 |
| 9 | 9,4 | 10,2 | -0,8 |
| 10 | 8,9 | 9,3 | -0,4 |
| 11 | 7,9 | 10,2 | -2,3 |
| 12 | 8,5 | 9,5 | -1 |
| Media | 8,4 | 10,2 | -1,7 |
| \(S\) | 0,8 | 0,9 | 1,2 |
Utilizando [est_m2md], podemos escribir:
\[\begin{aligned} P(t_{n-1;\alpha/2}\leq t_{n-1} \leq t_{n-1;1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(t_{n-1;\alpha/2}\leq \frac{\overline{d}-\delta}{S_{d}/\sqrt{n}}\leq t_{n-1;1-\alpha/2}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg(-\overline{d} + t_{n-1;\alpha/2} \frac{S_{d}}{\sqrt{n}} \leq -\delta\leq-\overline{d} + t_{n-1;1-\alpha/2} \frac{S_{d}}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \end{aligned}\] \[{ P\bigg(\overline{d} - t_{n-1;1-\alpha/2} \frac{S_{d}}{\sqrt{n}} \leq \delta \leq \overline{d} - t_{n-1;\alpha/2} \frac{S_{d}}{\sqrt{n}}\bigg)=1-\alpha}\]
Procediendo de igual forma que en los ejercicios anteriores, calculamos el intervalo de confianza teniendo en cuenta que \(t_{11;0.975}=2.20\), entonces:
\[\begin{aligned} \overline{d} - t_{n-1;1-\alpha/2} \frac{s_{d}}{\sqrt{n}} \leq & \delta & \leq \overline{d} - t_{n-1;\alpha/2} \frac{s_{d}}{\sqrt{n}} \nonumber \\ -1.7-2.20 \frac{1.2}{\sqrt{12}} \leq & \delta & \leq -1.7 - (-2.20) \frac{1.2}{\sqrt{12}} \nonumber \\ -2.46 \leq & \delta & \leq -0.93 \end{aligned}\]
Dado que hemos definido \(d=I-II\), la conclusión es que la cubierta I tiene un menor desgaste que la cubierta II, ya que el intervalo de confianza no incluye al cero porque sus límites son valores negativos (-2,46mm y -0,93mm). Si hubiésemos planteado \(d=II-I\), la conclusión sería que la cubierta II tiene mayor desgaste que la cubierta I.
Intervalos para la Proporción Poblacional
Sea una población dicotómica (Bernoulli), con \(N\) elementos, de los cuales \(k\) tienen una determinada propiedad. Entonces podemos definir al parámetro proporción poblacional \(\pi=k/N\), el cual es desconocido y se pretende estimar a partir de una muestra de tamaño \(n\). El estimador \(P=X/n\), donde \(X\) es el número de elementos con la propiedad deseada (éxitos) en la muestra, se denomina proporción muestral.
Teniendo en cuenta que \(X\) se distribuye como una distribución binomial (porque expresa la cantidad de éxitos en pruebas repetidas), con esperanza \(n\pi\) y varianza \(n\pi(1-\pi)\), si el tamaño de la muestra es lo suficiente grande entonces, por el TCL podemos escribir que:
\[\begin{aligned} \label{estadistico_p} \frac{P-\pi}{\sqrt{\pi(1-\pi)/n}}\sim N(0,1) \end{aligned}\]
Por el Teorema de De Moivre - Laplace, que plantea lo siguiente:
Si tenemos que \(X\) es una variable aleatoria binomial de parámetros \(n\) y \(p\), \(X \sim B(n,p)\), entonces “\(X\)” se puede aproximar a una distribución normal de media \(\mu=n\cdot p\) y desviación típica \(\sigma=\sqrt{n\cdot p \cdot (1-p)}\) si y sólo si se cumplen las siguientes condiciones:
\(n\geq 30\)
\(n\cdot p\geq 5\) y \(n\cdot (1-p)\geq 5\)
entonces, la variable binomial \(X \sim B(n,p)\) se aproxima a la variable normal \(X \sim N(n\cdot p,\sqrt{n\cdot p \cdot (1-p)})\)
De modo que, cuando se cumplen las condiciones de \(n\geq 30\), \(np\geq 5\) y \(n(1-p)\geq 5\), la aproximación anterior es adecuada y se emplea para construir el intervalo de confianza. Veamos a continuación el intervalo de confianza según se trate de una proporción poblacional o de la diferencia de proporciones de dos poblaciones.
Intervalos para la Proporción de una Población
Problema Resuelto 2.6. El Departamento de Control de Calidad de una empresa quiere estimar el verdadero valor de la proporción de productos defectuosos, para saber si necesita realizar ajustes en la línea de producción, o no. En caso de superar el 7%, debería realizar ajustes. Con este fin toma una muestra aleatoria de 80 productos encontrando que 15 de ellos tienen algún defecto. ¿Debe el departamento de control de calidad realizar algún ajuste? Utilizar un nivel de confianza del 90%.
Solución
Estamos ante un planteo con una muestra considerada grande y, por el TCL, el estadístico para la proporción es:
\[\begin{aligned} \frac{P-\pi}{\sqrt{\pi(1-\pi)/n}}\sim N(0,1) \end{aligned}\]
Para poder hacer uso de este estadístico se deben cumplir las condiciones \(nP>5\) y \(n(1-P)>5\), en este caso:
\[\begin{aligned} n\cdot p=80 \cdot \frac{15}{80}=15&>&5 \nonumber \\ n(1-p)=80 \cdot (1-\frac{15}{80})=65&>&5 \end{aligned}\]
Ahora podemos operar de forma similar a los problemas anteriores, es decir:
\[\begin{aligned} P(Z_{\alpha/2}\leq Z \leq Z_{1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(Z_{\alpha/2}\leq \frac{P-\pi}{\sqrt{\pi(1-\pi)/n}}\leq Z_{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando de la ecuación anterior surge que:
\[\begin{aligned} P\bigg(Z_{\alpha/2} \sqrt{\pi(1-\pi)/n} \leq (P-\pi) \leq Z_{1-\alpha/2} \sqrt{\pi(1-\pi)/n}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg( -P+Z_{\alpha/2} \sqrt{\pi(1-\pi)/n} \leq -\pi \leq - P+Z_{1-\alpha/2} \sqrt{\pi(1-\pi)/n}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg(P-Z_{1-\alpha/2} \sqrt{\pi(1-\pi)/n} \leq \pi \leq P-Z_{\alpha/2} \sqrt{\pi(1-\pi)/n}\bigg)\!=\; & 1-\alpha \nonumber \\ \end{aligned}\]
Como vemos, \(\pi\) aún sigue contenido en los extremos de la desigualdad. Para superar esta situación deberíamos plantear una ecuación de segundo grado. Sin embargo, si reemplazamos \(\pi\) por \(P\) en dichos extremos, se obtiene una aproximación muy razonable a los resultados que buscamos, por lo que planteamos:
\[{ P\bigg( P-Z_{1-\alpha/2} \sqrt{P(1-P)/n} \leq \pi \leq P-Z_{\alpha/2} \sqrt{P(1-P)/n}\bigg)=1-\alpha}\]
Sabiendo que \(P\) se define como la cantidad de éxitos sobre el total de casos de la muestra, entonces \(p=\frac{15}{80}=0.19\) tenemos:
\[\begin{aligned} p-Z_{1-\alpha/2} \sqrt{p(1-p)/n} \leq &\pi& \leq p-Z_{\alpha/2} \sqrt{p(1-p)/n} \nonumber \\ 0.19-1.64 \sqrt{0.19(1-0.19)/80} \leq & \pi & \leq 0.19-(-1.64) \sqrt{0.19(1-0.19)/80} \nonumber \\ 0.12\leq & \pi & \leq 0.26 \end{aligned}\]
Por lo tanto, con un nivel de confianza del 90%, el intervalo \([0.12; 0.26]\) contendrá el verdadero valor del parámetro poblacional \(\pi\). Esto significa que, el Departamento de Control de Calidad debe realizar algún ajuste porque el intervalo de estimación no contiene el valor \(0.07\) de defectuosos, lo cual indica que el porcentaje de defectuosos excede ese valor, ya que el intervalo se encuentra a su derecha.
Gráficamente es:
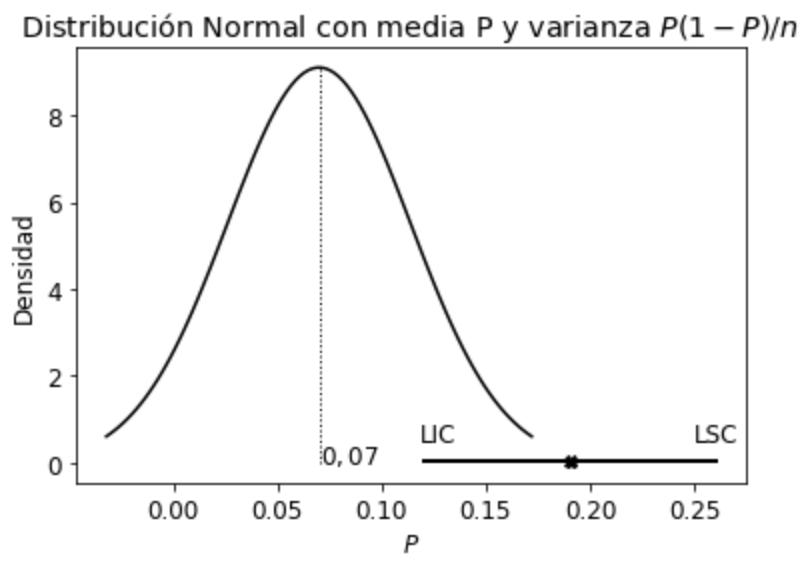
donde la distribución centrada en \(0.07\) corresponde a la distribución esperada por el Departamento de Control de Calidad (que no necesariamente es la verdadera distribución poblacional). Como el intervalo de confianza no incluye la media de la distribución esperada por dicho departamento, entonces se deben hacer los ajustes necesarios para que la producción de defectuosos disminuya y así corregir el problema. Por cierto que, podría haber existido un problema de muestreo, o bien muy “mala suerte” al seleccionar una muestra que no contiene el parámetro poblacional. Suponiendo que no existieron problemas de muestreo, y como es poco probable (10%) que hayamos seleccionado una “mala” muestra, entonces concluimos que se deben realizar los ajustes necesarios en la línea de producción.
Una consideración adicional, es que los límites del intervalo de confianza, en el caso de \(\pi\), nunca deberán estar fuera del rango \([0,1]\), dado que estamos trabajando con proporciones, las cuales están definidas siempre entre 0 y 1.
Intervalos para la Diferencia de dos Proporciones Poblacionales
Sean dos poblaciones con una misma variable dicotómica cada una, de las que extraemos sendas muestras de tamaño grande, \(n_{1}\) y \(n_{2}\), entonces podemos escribir:
\[\begin{aligned} \frac{P_{1}-\pi_{1}}{\sqrt{\pi_{1}(1-\pi_{1})/n_{1}}}\sim N(0,1) \nonumber \\ \frac{P_{2}-\pi_{2}}{\sqrt{\pi_{2}(1-\pi_{2})/n_{2}}}\sim N(0,1) \end{aligned}\] por lo tanto, \(P_{1}\) y \(P_{2}\) se distribuyen:
\[\begin{aligned} P_{1}\sim N(\pi_{1},\pi_{1}(1-\pi_{1})/n_{1}) \nonumber \\ P_{2}\sim N(\pi_{2},\pi_{2}(1-\pi_{2})/n_{2}) \end{aligned}\]
Restando ambas variables aleatorias, teniendo en cuenta que si las variables \(P_{1}\) y \(P_{2}\) son independientes, la varianza es \(V(P_{1}-P_{2})=V(P_{1})+V(p_{2})\), entonces podemos escribir:
\[\begin{aligned} (P_{1}-P_{2})\sim N((\pi_{1}-\pi_{2}),\pi_{1}(1-\pi_{1})/n_{1}+\pi_{2}(1-\pi_{2})/n_{2}) \end{aligned}\] que es el estadístico para la diferencia de dos proporciones de variables independientes.
Estandarizando tenemos:
\[\begin{aligned} \label{estadistico_p2mi} \frac{(P_{1}-P_{2})-(\pi_{1}-\pi_{2})}{\sqrt{\pi_{1}(1-\pi_{1})/n_{1}+\pi_{2}(1-\pi_{2})/n_{2}}}\sim N(0,1) \end{aligned}\] que se utiliza para armar el intervalo de confianza de dos proporciones.
Problema Resuelto 2.7. En una fábrica de componentes de computadora donde hay instaladas dos líneas de producción, se tomaron muestras aleatorias de \(n_{1}=200\) componentes de la primera línea, y se encontraron 17 unidades defectuosas; y de \(n_{2}=150\) de la segunda línea de producción en la que se hallaron 10 componentes defectuosos. Si se compara la proporción de defectuosos de ambas líneas, ¿qué conclusión puede obtener a un nivel de confianza del 95%?
Solución
Si se cumplen las condiciones \(nP>5\) y \(n(1-P)>5\) para cada una de las muestras, entonces se puede usar el estadístico [estadistico_p2mi] para estimar un intervalo de confianza de la diferencia de proporciones.
\[\begin{aligned} n_{1}p_{1}=200 \cdot \frac{17}{200}=17&>&5 \nonumber \\ n_{1}(1-_{1})=200 \cdot (1-\frac{17}{200})=183&>&5 \nonumber \\ n_{2}p_{2}=150 \cdot \frac{10}{150}=10&>&5 \nonumber \\ n_{2}(1-p_{2})=150 \cdot (1-\frac{10}{150})=140&>&5 \end{aligned}\]
Luego,
\[\begin{aligned} P(Z_{\alpha/2}\leq Z \leq Z_{1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(Z_{\alpha/2}\leq \frac{(P_{1}-P_{2})-(\pi_{1}-\pi_{2})}{\sqrt{\pi_{1}(1-\pi_{1})/n_{1}+\pi_{2}(1-\pi_{2})/n_{2}}} \leq Z_{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando \((\pi_{1}-\pi_{2})\) de la desigualdad y realizando la aproximación de reemplazar \(\pi\) por \(P\), tenemos:
\[\begin{aligned} P\bigg(Z_{\alpha/2}\leq \frac{(P_{1}-P_{2})-(\pi_{1}-\pi_{2})}{\sqrt{\frac{P_{1}(1-P_{1})}{n_{1}}+\frac{P_{2}(1-P_{2})}{n_{2}}}} \leq Z_{1-\alpha/2}\bigg)=1-\alpha \nonumber \\ P\bigg(Z_{\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \leq (P_{1}-P_{2})-(\pi_{1}-\pi_{2}) \leq Z_{1-\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \bigg)=1-\alpha \nonumber \\ P\bigg(-(P_{1}-P_{2})+Z_{\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \leq -(\pi_{1}-\pi_{2}) \leq -(P_{1}-P_{2})+Z_{1-\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \bigg)=1-\alpha \nonumber \end{aligned}\] \[{ P\bigg((P_{1}-P_{2})-Z_{1-\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \leq (\pi_{1}-\pi_{2}) \leq (P_{1}-P_{2})-Z_{\alpha/2} \sqrt{\widehat{\sigma}_{(P_{1}-P_{2})}} \bigg)=1-\alpha}\] donde \(\widehat{\sigma}_{(P_{1}-P_{2})}=\frac{P_{1}(1-P_{1})}{n_{1}}+\frac{P_{2}(1-P_{2})}{n_{2}}\).
La estimación por intervalo es:
\[\begin{aligned} (p_{1}-p_{2})-Z_{1-\alpha/2} \sqrt{\widehat{\sigma}_{(p_{1}-p_{2})}} \leq &(\pi_{1}-\pi_{2})& \leq (p_{1}-p_{2})-Z_{\alpha/2} \sqrt{\widehat{\sigma}_{(p_{1}-p_{2})}} \nonumber \\ (0.085-0.067)-1.96 \sqrt{0.000804} \leq & (\pi_{1}-\pi_{2}) & \leq (0.085-0.067)-(-1.96) \sqrt{0.000804} \nonumber \\ -0.0372 \leq & (\pi_{1}-\pi_{2}) & \leq 0.0739 \nonumber \\ \end{aligned}\] donde \(\widehat{\sigma}_{p_{1}-p_{2}}=0.000804\).
Dado que el cero está incluido en el intervalo de confianza, la conclusión es que no existe diferencia significativa de la proporción de defectuosos entre las líneas de producción, a un nivel de confianza de 95%.
Intervalos para la Varianza Poblacional
Nuevamente, aquí tendremos en cuenta dos situaciones, según estemos en presencia de una o de dos poblaciones.
Intervalos para la Varianza de una Población
Cuando se trata de estimar intervalos de confianza para la varianza de una población, extraemos una muestra y hacemos uso del estadístico \(\chi^{2}\) que viene dado en [estadistico_chi], bajo el supuesto de poblaciones normales. Es decir:
\[\begin{aligned} \frac{(n-1)S^{2}}{\sigma^{2}} \sim \chi^{2}_{n-1} \end{aligned}\]
Problema Resuelto 2.8. Un agente de bolsa debe asesorar a un nuevo inversor con relación al precio de las acciones de una empresa energética de España (Iberdrola), no sólo en su promedio sino también en su variabilidad. Para ello computó los valores diarios de cotizaciones (en euros) durante los primeros 24 días del mes anterior y obtuvo los resultados que aparecen en la tabla. ¿Qué información podrá dar el agente de bolsa a un nivel de confianza del 95%? Suponer que la variable se distribuye normalmente en la población.
| Día | Cotización (€) | Día | Cotización (€) |
|---|---|---|---|
| 26-may-2020 | 9.252 | 11-jun-2020 | 9.682 |
| 27-may-2020 | 9.604 | 12-jun-2020 | 9.750 |
| 28-may-2020 | 9.618 | 15-jun-2020 | 9.712 |
| 29-may-2020 | 9.688 | 16-jun-2020 | 10.010 |
| 01-jun-2020 | 9.700 | 17-jun-2020 | 10.015 |
| 02-jun-2020 | 9.932 | 18-jun-2020 | 9.962 |
| 03-jun-2020 | 10.115 | 19-jun-2020 | 10.190 |
| 04-jun-2020 | 9.958 | 22-jun-2020 | 10.130 |
| 05-jun-2020 | 10.030 | 23-jun-2020 | 10.285 |
| 08-jun-2020 | 10.130 | 24-jun-2020 | 9.998 |
| 09-jun-2020 | 10.150 | 25-jun-2020 | 10.110 |
| 10-jun-2020 | 9.986 | 26-jun-2020 | 10.040 |
| \(\overline{X}=9.919\) | |||
| \(S^{2}=0.059\) | |||
Solución
El agente puede proporcionar información, sobre la media y la varianza poblacional. Empecemos analizando la media poblacional. Dado que descocemos la varianza poblacional y tenemos un tamaño de muestra inferior a 30, el intervalo de confianza que se debe calcular para la media poblacional es:
\[\begin{aligned} P\bigg(\overline{X} - t_{n-1;1-\alpha/2} \frac{S}{\sqrt{n}} \leq \mu \leq \overline{X} - t_{n-1;\alpha/2} \frac{S}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Con los datos de la muestra se obtiene que \(\overline{X}=9.92\) y que \(S=0.242\), entonces el intervalo para la media poblacional con un nivel de confianza del 95% es:
\[\begin{aligned} \overline{x} - t_{n-1;1-\alpha/2} \frac{s}{\sqrt{n}} \leq &\mu &\leq \overline{x} - t_{n-1;\alpha/2} \frac{s}{\sqrt{n}} \nonumber \\ 9.92- 2.069 \frac{0.242}{\sqrt{24}} \leq &\mu& \leq 9.92 - 2.069 \frac{0.242}{\sqrt{24}} \nonumber \\ 9.816 \leq &\mu& \leq 10.021 \end{aligned}\]
Cuando tenemos una muestra, y queremos estimar un intervalo de confianza de la varianza, debemos partir del estadístico [estadistico_chi] y plantear:
\[\begin{aligned} P(\chi^{2}_{n-1;\alpha/2}\leq \chi^{2}_{n-1} \leq \chi^{2}_{n-1;1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(\chi^{2}_{n-1;\alpha/2}\leq \frac{(n-1)S^{2}}{\sigma^{2}} \leq \chi^{2}_{n-1;1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando \(\sigma^{2}\) de la desigualdad:
\[\begin{aligned} P\bigg(\frac{\chi^{2}_{n-1;\alpha/2}}{(n-1)S^{2}}\leq \frac{1}{\sigma^{2}} \leq \frac{\chi^{2}_{n-1;1-\alpha/2}}{(n-1)S^{2}}\bigg)\!=\; & 1-\alpha \nonumber \end{aligned}\] \[{ P\bigg(\frac{(n-1)S^{2}}{\chi^{2}_{n-1;1-\alpha/2}}\leq \sigma^{2} \leq \frac{(n-1)S^{2}}{\chi^{2}_{n-1;\alpha/2}}\bigg)=1-\alpha}\]
Reemplazando la varianza muestral, y teniendo en cuenta que los grados de libertad con los que debemos trabajar son \(n-1=23\), donde \(n\) es el tamaño de la muestra, obtenemos:
\[\begin{aligned} \frac{(n-1)s^{2}}{\chi^{2}_{n-1;1-\alpha/2}}\leq &\sigma^{2} &\leq \frac{(n-1)s^{2}}{\chi^{2}_{n-1;\alpha/2}} \nonumber \\ \frac{(24-1)0.059}{\chi^{2}_{24-1;0.975}}\leq & \sigma^{2} & \leq \frac{(24-1)0.059}{\chi^{2}_{24-1;0.025}} \nonumber \\ \frac{(24-1)0.059}{38.076}\leq & \sigma^{2} & \leq \frac{(24-1)0.059}{11.689} \nonumber \\ 0.035 \leq & \sigma^{2} & \leq 0.115 \end{aligned}\]
Por lo tanto, el agente de bolsa dirá a su cliente que, el precio promedio puntual de la acción es 9,919 € y que, con un 95% de nivel de confianza se encuentra entre 9,816€ y 10,021€. La varianza, por su parte, oscila, con un 95% de confianza, entre 0,035 y 0,115.
La resolución de la segunda parte de este problema en Python es (se deja a cargo del lector la resolución de la primera parte):
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import chi2
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Nivel de confianza
nivel_conf=0.95
# Datos muestrales
data=[9.252,9.604,9.618,9.688,9.7,9.932,10.115,9.958,10.03,
10.13,10.15,9.986,9.682,9.75,9.712,10.01,10.015,9.962,
10.19,10.13,10.285,9.998,10.11,10.04]
def ic(data,nivel_conf):
n = len(data)
chi_1 = chi2.ppf(nivel_conf+(1-nivel_conf)/2,n-1)
chi_2 = chi2.ppf(1-(nivel_conf+(1-nivel_conf)/2),n-1)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
var=data_sd**2
lim_inf=(n-1)*var/chi_1
lim_sup=(n-1)*var/chi_2
return lim_inf,lim_sup,data_mean,var,n
lim_inf,lim_sup,data_mean,var,n = ic(data,nivel_conf)
print("Media Muestral =",data_mean)
print("Varianza Muestral =",var)
print("n Muestral")
print("Intervalo de confianza: ","[",lim_inf,";",lim_sup,"]")
Media Muestral = 9.918624999999999
Varianza Muestral = 0.05856685326086955
n Muestral
Intervalo de confianza: [ 0.03537794968269136 ; 0.11524418370529599 ]Intervalos para la Comparación de Varianzas de dos Poblaciones
En el caso que se quiera estimar intervalos para comparar varianzas de dos poblaciones, se hace uso del estadístico \(F\) ([estadistico_f1]):
\[\begin{aligned} \frac{S_{1}^{2}}{S_{2}^{2}}\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} \sim F_{n_{1}-1,n_{2}-1} \nonumber \end{aligned}\]
Problema Resuelto 2.9. La resistencia del hormigón es un factor fundamental en la construcción. Una empresa dedicada a la fabricación de hormigón está investigando acerca de un nuevo producto el cual, aseguran los ingenieros, tendría una mayor resistencia que el actual producto de mercado, y con una menor variabilidad. Para verificar el supuesto de los ingenieros se tomaron dos muestras aleatorias, una de cada tipo de hormigón, y se las sometió a pruebas de resistencia, con los siguientes resultados:
| Hormigón | Actual | 22,6 | 24,1 | 24,9 | 22,8 | 22,4 | ||
| Nuevo | 31,0 | 29,3 | 30,8 | 29,1 | 30,3 | 30,5 | 30,3 |
Suponiendo que ambas poblaciones se distribuyen normalmente, determinar si existe diferencia significativa, a un nivel de confianza del 99%, en la variabilidad de la resistencia de ambos tipos de hormigón.
Solución
Dado que en esta ocasión estamos trabajando con dos muestras y suponemos que ambas poblaciones se distribuyen normales, entonces vamos a partir del estadístico \(F\) ([estadistico_f1]):
\[\begin{aligned} P(F_{n_{1}-1;n_{2}-1}^{\alpha/2}\leq F_{n_{1}-1;n_{2}-1} \leq F_{n_{1}-1;n_{2}-1}^{1-\alpha/2})\!=\; & 1-\alpha \nonumber \\ P\bigg(F_{n_{1}-1;n_{2}-1}^{\alpha/2}\leq \frac{S_{1}^{2}}{S_{2}^{2}}\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} \leq F_{n_{1}-1;n_{2}-1}^{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Despejando, dentro de la desigualdad, la relación \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\):
\[\begin{aligned} P\bigg(F_{n_{1}-1;n_{2}-1}^{\alpha/2} \frac{S_{2}^{2}}{S_{1}^{2}} \leq \frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} \leq F_{n_{1}-1;n_{2}-1}^{1-\alpha/2}\frac{S_{2}^{2}}{S_{1}^{2}} \bigg)\!=\; & 1-\alpha \nonumber \end{aligned}\] \[{ P\bigg(\frac{1}{F_{n_{1}-1;n_{2}-1}^{1-\alpha/2}} \frac{S_{1}^{2}}{S_{2}^{2}} \leq \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} \leq \frac{1}{F_{n_{1}-1;n_{2}-1}^{\alpha/2}}\frac{S_{1}^{2}}{S_{2}^{2}} \bigg)=1-\alpha}\]
Calculando las varianzas muestrales, tenemos: \(s_{actual}^{2}=1.183\) y \(s_{nuevo}^{2}=0.521\) respectivamente. Por otra parte, dado que el tamaño de la muestra para el hormigón actual es de 5 y para el hormigón nuevo es de 7, entonces podemos escribir:
\[\begin{aligned} \frac{1}{F_{n_{1}-1;n_{2}-1}^{1-\alpha/2}} \frac{s_{1}^{2}}{s_{2}^{2}} \leq & \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} & \leq \frac{1}{F_{n_{1}-1;n_{2}-1}^{\alpha/2}}\frac{s_{1}^{2}}{s_{2}^{2}} \nonumber \\ \frac{1}{F_{5-1;7-1}^{0.995}} \frac{1.183}{0.521} \leq & \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} & \leq \frac{1}{F_{5-1;7-1}^{0.005}}\frac{1.183}{0.521} \nonumber \\ \frac{1}{12.02} \cdot 2.27\leq & \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} & \leq \frac{1}{0.04} \cdot 2.27 \nonumber \\ 0.19 \leq & \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} & \leq 56.75 \end{aligned}\]
Cuando dos varianzas poblacionales son iguales, el cociente \(\sigma_{1}/\sigma_{2}=1\), de lo contrario las varianzas son diferentes. Como el valor uno está incluido dentro del intervalo de confianza, entonces no hay diferencias estadísticamente significativas de la resistencia entre los distintos tipos de hormigón, a un nivel de confianza del 99%.
Resumen de Intervalos de Confianza

Pruebas de Hipótesis Paramétricas
El propósito del análisis estadístico inferencial es reducir el nivel de incertidumbre para la toma de decisiones. La prueba de hipótesis es una herramienta analítica efectiva para obtener información valiosa de diversos parámetros o características de la población.
La prueba de hipótesis (o test de hipótesis) comienza con una suposición, llamada hipótesis, que hacemos con respecto a un parámetro de la población.
Definición 3.1 (Hipótesis Nula). Es la suposición que deseamos rechazar, generalmente se conoce como hipótesis nula y se simboliza por \(H_{0}\).
Definición 3.2 (Hipótesis Alternativa). Es la hipótesis que, generalmente, se quiere demostrar. Esta hipótesis es opuesta, y difiere de \(H_{0}\) y se denota como \(H_{1}\).
Las hipótesis \(H_{0}\) y \(H_{1}\) son mutuamente excluyentes.
Por cada tipo de test de hipótesis se puede determinar una prueba estadística apropiada que se utiliza para medir la proximidad del estadístico de la muestra (como un promedio) con respecto al estadístico de la hipótesis nula. Cuando se realizan supuestos acerca de la distribución de la población (por ejemplo, que se distribuye normal) tenemos una Prueba de Hipótesis Paramétrica, mientras que si no se hacen supuestos sobre la distribución de la población, se denomina Prueba de Hipótesis No Paramétrica.
A partir de un nivel de probabilidad acumulado en la distribución del estadístico de la prueba que se decidió utilizar, se determinan dos regiones para el dominio de dicha distribución: una región de rechazo y otra de no rechazo. Si el valor del estadístico cae en la zona de rechazo, se rechaza la hipótesis nula. De lo contrario esa hipótesis no se puede rechazar, como consecuencia, no se puede llegar, generalmente, a una conclusión estadísticamente significativa.
Para determinar ambas zonas, se deben establecer el/los valor/es crítico/s en la distribución estadística que divide/n la región del no rechazo (en la cual la hipótesis nula no se puede rechazar) de la región de rechazo. El tamaño de la región de rechazo (y por ende el de la región de no rechazo) depende de los valores críticos, que a su vez, está supeditado a un nivel de probabilidad acumulado que debe ser definido previamente.
En estas condiciones se pueden cometer dos tipo de errores:
Error de Tipo I: se rechaza la hipótesis nula cuando en realidad es verdadera.
Error de Tipo II: no se rechaza la hipótesis nula cuando en realidad es falsa.
Definición 3.3 (Nivel de Significancia). Es la probabilidad de ocurrencia del error de Tipo I, o sea el área bajo la curva de la función de distribución de probabilidad determinado por el dominio de la zona de rechazo.
A continuación se resumen diferentes situaciones posibles que se pueden presentar en una prueba de hipótesis
| Decisión | \(H_{0}\) Verdadera | \(H_{0}\) Falsa |
|---|---|---|
| Rechazar \(H_{0}\) | Error de Tipo I | Decisión Correcta |
| \(P(E_{I})=\alpha\) | \(P(DC)=1-\beta\) | |
| No Rechazar \(H_{0}\) | Decisión Correcta | Error de Tipo II |
| \(P(DC)=1-\alpha\) | \(P(E_{II})=\beta\) |
A la probabilidad de rechazar \(H_{0}\) cuando es falsa (\(1-\beta\)) se la conoce como Potencia de una prueba. El punto crítico viene determinado en la distribución del estadístico a partir del área del error de Tipo I (\(\alpha\)).
Se pueden plantear tres tipos de pruebas de hipótesis, que son los que determinan que el área de la zona de rechazo esté a uno de los lados de la función de distribución de probabilidad, o bien en las dos colas de la misma. Se trata de las siguientes situaciones:
| Unilateral derecha | Unilateral izquierda | Bilateral |
| \(H_{0}: \mu \leq \mu_{0}\) | \(H_{0}: \mu \geq \mu_{0}\) | \(H_{0}: \mu = \mu_{0}\) |
| \(H_{1}: \mu > \mu_{0}\) | \(H_{1}: \mu < \mu_{0}\) | \(H_{1}: \mu \neq \mu_{0}\) |
 |
 |
 |
Pruebas para la Media Poblacional
Tal como se desarrolló en el capítulo de intervalos de confianza, aquí también haremos la distinción de pruebas para una muestra y dos muestras. A su vez, en el caso de una muestra se presentarán dos posibles opciones, cuando se conoce la varianza poblacional y cuando ésta es desconocida. En el caso de dos muestras, diferenciaremos entre muestras independientes y dependientes.
Prueba para la Media de una Población
Supongamos que tenemos una variable aleatoria \(X\) con media \(\mu\) y varianza \(\sigma^{2}\), entonces por el TCL, cuando \(n\) es grande, podemos decir que:
\[\begin{aligned} \overline{X} \sim N(\mu,\sigma^{2}/n) \end{aligned}\]
O bien: \[\label{estadistico_z} { \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)}\]
Varianza poblacional conocida, poblaciones normales o muestras mayores que 30 para cualquier distribución
El estadístico ([estadistico_z]) se utiliza cuando la varianza poblacional es conocida y la muestra: (i) es de cualquier tamaño y fue extraída de una población normal, o (ii) es proveniente de una población con cualquier distribución y su tamaño es mayor o igual a 30.
En el caso que se conozca la varianza de la población, que se sabe es normal, o bien se tiene que la muestra supera el tamaño de \(n=30\) sin importar la distribución poblacional, el estadístico que se usa para el planteo de la hipótesis es el ([estadistico_z]).
Problema Resuelto 3.1. El gerente de una cadena de farmacias ha informado al Directorio que en las últimas semanas han aumentado las ventas de vacunas contra la gripe en relación al histórico del mismo período, que se situaba en 25,2 vacunas. Para corroborar lo informado por el gerente, se toma una muestra de 67 farmacias y se obtienen los siguientes datos:
| N | 67 |
| \(\overline{x}\) | \(28,54\) |
Suponiendo que la población se distribuye normal y que se conoce que \(\sigma=8.50\), responder:
¿Es razonable lo informado por el gerente?. Trabajar con un \(\alpha=0.01\).
¿Cuál es la verdadera cantidad promedio de vacunas vendidas? Estimar el parámetro poblacional planteando un intervalo de confianza a un nivel de (\(1-\alpha=0.95\))
Solución
Con las pruebas de hipótesis se busca determinar, en general, si un resultado muestral que aparece como diferente al que se esperaba (hipótesis), puede ser considerado como una indicación válida de que la hipótesis que habíamos asumido estaba errada (o no). En este problema, el gerente manifiesta que las ventas promedio semanal de las vacunas han aumentado y que ya no es el valor \(25,20\) que en la empresa tenían como cierto. De acuerdo a la muestra aleatoria extraída, las ventas promedio de las últimas semanas ascendieron a \(28,54\).
Surge entonces la pregunta sobre si ¿ese resultado es suficientemente demostrativo que el gerente tiene razón? Si nos atenemos a la comparación de los dos guarismos anteriores (un valor puntual de la media muestral, contra un valor tomado como cierto), tendríamos que decir que el funcionario está en lo cierto. Pero si reflexionamos y tenemos en cuenta que bien podría haber salido otra muestra distinta, con otro resultado, donde quizá la diferencia hubiese sido mucho menor (por ejemplo \(25,7\) vacunas), en ese caso ¿la conclusión hubiese sido la misma? Quizá sí, pero con mucho menor convencimiento. El núcleo de la prueba de hipótesis es entonces determinar ¿cuánto se debe alejar el resultado muestral con respecto de la hipótesis (\(25,2\)), para que podamos afirmar, con cierta confianza, que el promedio semanal de ventas de vacunas ha aumentado? En otros términos, ¿a partir de qué nivel de ventas promedio semanal de la muestra podremos decir que rechazamos la hipótesis nula (\(H_{0}\)) que las ventas no han aumentado? Eso es lo que trataremos de determinar en lo que sigue de la resolución.
Dado que suponemos que la población es normal, que conocemos la varianza poblacional, y que estamos interesados en hacer una prueba sobre la media poblacional, debemos usar el estadístico [estadistico_z]. Generalmente, se suele plantear en \(H_{0}\) aquella hipótesis que queremos rechazar y en \(H_{1}\) la que queremos demostrar. Como en este caso estamos interesados en demostrar que han aumentado las ventas de vacunas en relación al mismo período histórico, entonces planteamos la prueba de la siguiente forma:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \mu &\leq& 25.20 \nonumber \\ H_{1}\!:\; & \quad \mu &>& 25.20 \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\] donde el estadístico es:
\[\begin{aligned} Z_{obs}\!=\; & \frac{\overline{x}-\mu_{0}}{\sigma/\sqrt{n}} \nonumber \\ \!=\; & \frac{28.54-25.20}{8.50/\sqrt{67}} \nonumber \\ \!=\; & 3.21 \end{aligned}\]
Como es una prueba del tipo unilateral derecha, tenemos la zona de rechazo a la derecha de la distribución. Es decir, que la zona de rechazo de la hipótesis nula viene dada por:
\[\begin{aligned} \textbf{ZR}=\lbrace Z \in \mathbb{R} \quad \vert \quad Z>Z_{crit} \rbrace \end{aligned}\]
Dado que estamos trabajando con un nivel de significancia (\(\alpha\)) del 1%, entonces el \(Z_{crit}=2.32\). En consecuencia, tenemos que:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z>Z_{crit} \rbrace \nonumber \\ \!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z>2.32\rbrace \Rightarrow Z_{obs}=3.21 \in \textbf{ZR} \end{aligned}\]
Por lo que se rechaza la hipótesis nula que el promedio de ventas de vacunas en el período analizado es inferior o igual a 25,2 vacunas vendidas semanalmente. En consecuencia, podemos decir que es correcta la afirmación del gerente, ya que el promedio superó significativamente (en términos estadísticos) al valor histórico.
Gráficamente es:
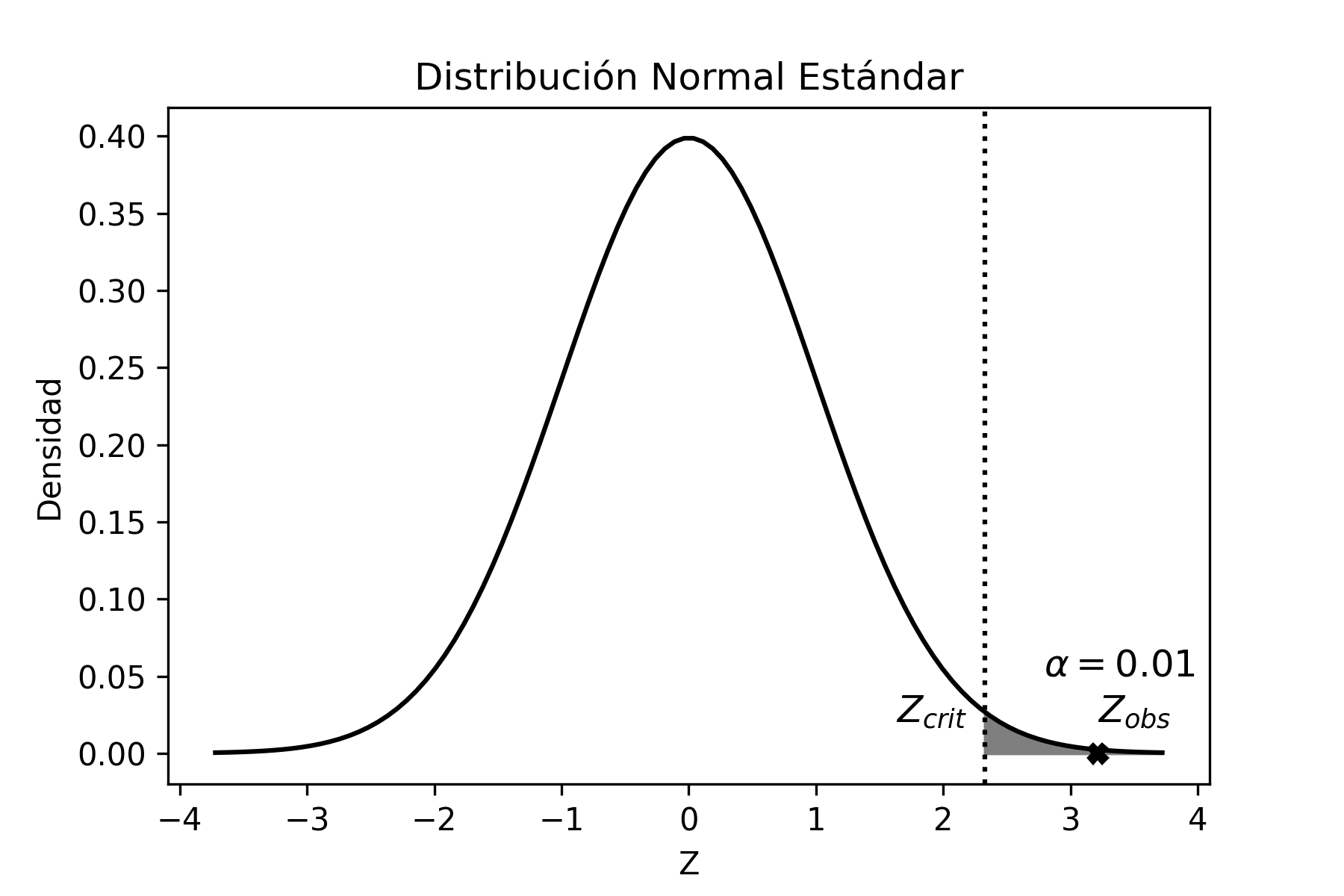
Para estimar la verdadera cantidad promedio de vacunas vendidas, haremos uso de una estimación por intervalo de confianza. Es por eso que utilizamos [ic_media], es decir:
\[\begin{aligned} \overline{x} - Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{x} - Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \nonumber \\ 28.54- 1.96 \frac{8.50}{\sqrt{67}} \leq \mu \leq 28.54 - (-1.96) \frac{8.50}{\sqrt{67}} \end{aligned}\]
Luego, con una confianza del 95%, el verdadero valor del parámetro poblacional, es decir, la cantidad semanal de vacunas vendidas, estará comprendido en el siguiente intervalo:
\[\begin{aligned} 26.50 \leq & \mu & \leq 30.57 \end{aligned}\]
El script para resolver el problema en Python es el siguiente:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Media poblacional bajo hipotesis nula
u0=25.20
# Varianza poblacional
var=8.50**2
# Nivel de significancia
alfa=0.01
# Datos muestrales
data=[32,35,24,46,41,34,30,38,26,27,29,28,22,30,26,26,28,
43,38,25,31,15,37,23,35,28,34,34,29,46,24,22,30,
44,33,18,30,23,7,37,36,18,36,39,25,30,27,29,10,14,
33,29,24,10,10,28,15,22,27,17,38,34,33,23,50,31,16]
#sides -- 1: dos colas; 2: una cola izquierda; 3: una cola derecha
sides=3
def prueba_z(data,u0,var,alfa,sides):
n = len(data)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
sigma2 = np.sqrt(var/n)
z_obs = (data_mean-u0)/sigma2
if sides==1 and z_obs<0:
p_value = norm.cdf(z_obs)
p_value = 2*p_value
tipo_p="bilateral"
elif sides==1 and z_obs>=0:
p_value = norm.cdf(z_obs)
p_value = 2*(1-p_value)
tipo_p="bilateral"
elif sides==2:
p_value = norm.cdf(z_obs)
p_value = p_value
tipo_p="unilateral izquierda"
elif sides==3:
p_value = norm.cdf(z_obs)
p_value = 1-p_value
tipo_p="unilateral derecha"
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return z_obs,p_value,conclusion,n,data_mean,data_sd,tipo_p
z_obs,p_value,conclusion,n,data_mean,data_sd,tipo_p = prueba_z(data,u0,var,alfa,sides)
print("Prueba de hipotesis",tipo_p)
print("Media Muestral =",data_mean)
print("S Muestral =",data_sd)
print("n =",n)
print("Nivel de significancia =",alfa)
print("Z observado =",z_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis unilateral derecha
Media Muestral = 28.53731343283582
S Muestral = 9.149148591302138
n = 67
Nivel de significancia = 0.01
Z observado = 3.2137750303611576
p valor = 0.0006550113510445099
Se rechaza la hipotesis nulaHay que tener en cuenta que existe una función “statsmodels.stats.weightstats.ztest” dentro del paquete “statsmodels” que calcula la prueba, pero no usa la varianza poblacional sino la varianza muestral, por lo tanto, si la muestra es chica, las diferencias pueden ser importantes. Por dicha razón, se genera en el código la función llamada “prueba_z” la cual tiene como parámetro de entrada la varianza poblacional, que se supone conocida.
Para calcular el intervalo de confianza, el código es:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Nivel de confianza
nivel_conf=0.95
# Varianza poblacional
var=8.50**2
# Datos muestrales
data=[32,35,24,46,41,34,30,38,26,27,29,28,22,30,26,26,28,
43,38,25,31,15,37,23,35,28,34,34,29,46,24,22,30,
44,33,18,30,23,7,37,36,18,36,39,25,30,27,29,10,14,
33,29,24,10,10,28,15,22,27,17,38,34,33,23,50,31,16]
def ic(data,var,nivel_conf):
n = len(data)
z = norm.ppf(nivel_conf+(1-nivel_conf)/2)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
sigma=np.sqrt(var)
lim_inf=data_mean-z*sigma/n**0.5
lim_sup=data_mean+z*sigma/n**0.5
return lim_inf,lim_sup,z,data_mean,data_sd,n
lim_inf,lim_sup,z,data_mean,data_sd,n = ic(data,var,nivel_conf)
print("Media Muestral =",data_mean)
print("S Muestral =",data_sd)
print("n muestral =",n)
print("z =", z)
print("Intervalo de confianza: ","[",lim_inf,";",lim_sup,"]")
Media Muestral = 28.53731343283582
S Muestral = 9.149148591302138
n muestral = 67
z = 1.959963984540054
Intervalo de confianza: [ 26.502007889763977 ; 30.572618975907663 ]Varianza poblacional desconocida, poblaciones normales y no normales
Cuando la varianza poblacional es desconocida, el estadístico que se usa en la prueba de hipótesis es el de la ecuación [estadistico_t].
\[{ \frac{\overline{X}-\mu}{S/\sqrt{n}} \sim t_{n-1}}\]
Problema Resuelto 3.2. Una concesionaria vende en promedio \(7.05\) autos por mes y por sucursal. Durante el último mes implementó una oferta y el número de autos vendidos en una muestra de 10 sucursales fue: 12, 10, 12, 5, 7, 13, 8, 11, 8 y 10. A un nivel de significación de 5% y suponiendo que las ventas siguen una distribución normal, ¿se puede decir que la concesionaria incrementó la venta promedio mensual de automóviles por sucursal?
Solución
En este caso, dado que la varianza poblacional no se conoce y como queremos demostrar que las ventas promedio mensual están por encima de \(7,05\) autos, podemos plantear la siguiente prueba:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \mu &\leq& 7.05 \nonumber \\ H_{1}\!:\; & \quad \mu &>& 7.05 \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Calculando, con los datos muestrales, llegamos a que \(\overline{X}=9.60\) y que \(S=2.55\), por lo que
\[\begin{aligned} t_{n-1}^{obs}\!=\; & \frac{\overline{x}-\mu_{0}}{s/\sqrt{n}} \nonumber \\ \!=\; & \frac{9.60-7.05}{2.55/\sqrt{10}} \nonumber \\ \!=\; & 3.16 \end{aligned}\]
Por tratarse de una prueba del tipo unilateral derecha, tenemos que la zona de rechazo de \(H_{0}\) estará en la cola derecha de la distribución, es decir:
\[\begin{aligned} \textbf{ZR}=\lbrace t_{n-1} \in \mathbb{R} \quad \vert \quad t_{n-1}>t_{n-1}^{crit} \rbrace \end{aligned}\]
Como estamos trabajando con un nivel de significancia (\(\alpha\)) del 5%, y la cantidad de grados de libertad viene dado por \(n-1=9\), donde \(n\) es el tamaño de la muestra, entonces el \(t_{9}^{crit}=1.83\). En consecuencia, tenemos que:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace t_{n-1} \in \mathbb{R} \quad \vert \quad t_{n-1}>t_{n-1}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace t_{n-1} \in \mathbb{R} \quad \vert \quad t_{9}>1.83\rbrace \Rightarrow t_{obs}=3.16 \in \textbf{ZR} \end{aligned}\]
Con este resultado, rechazamos la hipótesis nula de que la media poblacional es igual o menor a 7,05, y por lo tanto, podemos decir que la concesionaria aumentó el promedio mensual de autos vendidos al implementar la oferta.
Gráficamente tenemos:
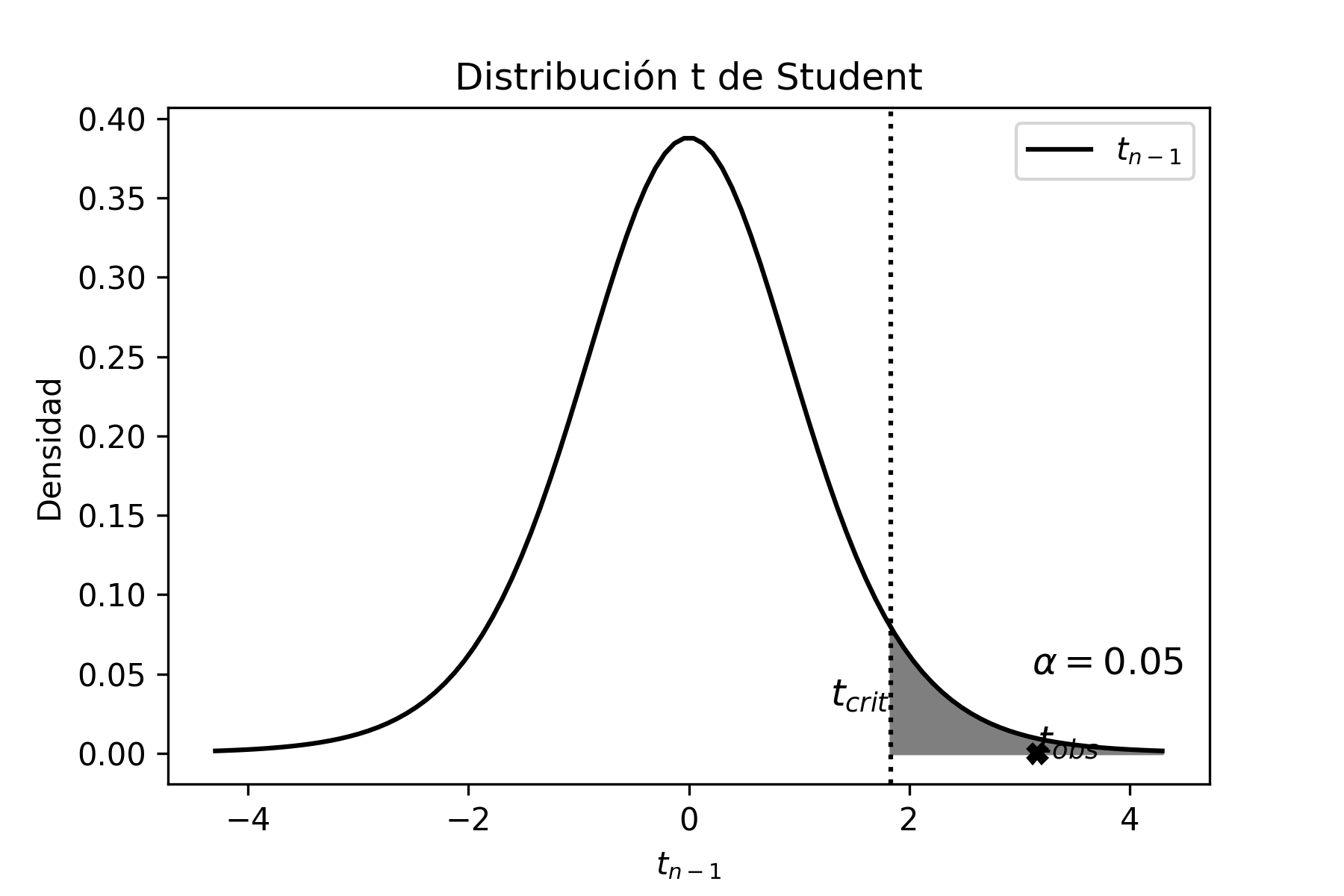
Para resolver el ejercicio en Python, aplicamos el siguiente código:
# Librerias
from scipy import stats
import numpy as np
import statistics
from statistics import stdev
# Media poblacional bajo hipotesis nula
u0=7.05
# Nivel de significancia
alfa=0.05
# Datos muestrales
data=[12, 10, 12, 5, 7, 13, 8, 11, 8 , 10]
#sides -- 1: dos colas; 2: una cola izquierda; 3: una cola derecha
sides=3
def prueba_t(data,u0,alfa,sides):
n = len(data)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
err_est=np.sqrt(data_sd**2/n)
t_obs = (data_mean-u0)/err_est
t = stats.t(n-1)
if sides==1 and t_obs<0:
p_value = t.cdf(t_obs)
p_value = 2*p_value
tipo_p="bilateral"
elif sides==1 and t_obs>=0:
p_value = t.cdf(t_obs)
p_value = 2*(1-p_value)
tipo_p="bilateral"
elif sides==2:
p_value = t.cdf(t_obs)
p_value = p_value
tipo_p="unilateral izquierda"
elif sides==3:
p_value = t.cdf(t_obs)
p_value = 1-p_value
tipo_p="unilateral derecha"
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return t_obs,p_value,conclusion,n,data_mean,data_sd,tipo_p
t_obs,p_value,conclusion,n,data_mean,data_sd,tipo_p = prueba_t(data,u0,alfa,sides)
print("Prueba de hipotesis",tipo_p)
print("Media Muestral =",data_mean)
print("S Muestral =",data_sd)
print("n =",n)
print("Nivel de significancia =",alfa)
print("t observado =",t_obs)
print("p valor = ",p_value)
# Conclusion de la prueba de hipotesis
if p_value < alfa:
print("Se rechaza la hipotesis nula")
else:
print("No se rechaza la hipotesis nula")
Prueba de hipotesis unilateral derecha
Media Muestral = 9.6
S Muestral = 2.5473297566057065
n = 10
Nivel de significancia = 0.05
t observado = 3.1655925239040577
p valor = 0.00572340229486179
Se rechaza la hipotesis nula
Para la solución de este problema a través de Python hicimos uso del concepto de p-valor, cuyo significado veremos más adelante.
Prueba para la Diferencia de Medias de dos Poblaciones
Muestras independientes
Sean \(X_{1}\) y \(X_{2}\) dos variables aleatorias independientes provenientes de muestras de tamaños \(n_{1}\) y \(n_{2}\), entonces por el TCL podemos escribir:
\[\begin{aligned} \overline{X}_{1} &\sim& N(\mu_{1},\sigma_{1}^{2}/n_{1}) \nonumber \\ \overline{X}_{2} &\sim& N(\mu_{2},\sigma_{2}^{2}/n_{2}) \nonumber \end{aligned}\]
Abordaremos tanto el caso de varianzas poblacionales conocidas, como la situación donde son desconocidas, pero se suponen iguales (\(\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}\)). Entonces restando ambas variables y estandarizando tenemos:
\[\begin{aligned} \overline{X}_{1} -\overline{X}_{2} &\sim& N \bigg(\mu_{1}-\mu_{2},V(\overline{X}_{1} -\overline{X}_{2}) \bigg) \nonumber \\ \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{V(\overline{X}_{1} -\overline{X}_{2})}} &\sim& N(0,1) \nonumber \end{aligned}\] \[\label{estadistico_m2ic} { \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}}} \sim N(0,1)}\] que es el estadístico a usar para la prueba de diferencias de medias con varianzas poblacionales conocidas.
En el caso de varianzas poblacionales desconocidas pero iguales, podemos escribir que
\[\begin{aligned} V(\overline{X}_{1}-\overline{X}_{2})=\sigma^{2} \bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}} \bigg) \end{aligned}\]
Por otra parte, sabemos que el mejor estimador para la varianza de la diferencia de medias es el promedio ponderado de las varianzas muestrales de los dos grupos, es decir:
\[\begin{aligned} \label{sp} S_{p}^{2}=\frac{(n_{1}-1)S_{1}^{2}+(n_{2}-1)S_{2}^{2}}{(n_{1}-1)+(n_{2}-1)} \end{aligned}\] entonces reemplazando [sp] en [estadistico_m2ic] llegamos a que
\[\label{estadistico_m2id} { \frac{(\overline{X}_{1} -\overline{X}_{2})-(\mu_{1}-\mu_{2})}{S_{p}\sqrt{1/n_{1} +1/n_{2}}} \sim t_{n_{1}+n_{2}-2}}\] que es el estadístico a utilizar en el caso de no conocer las varianzas poblacionales, bajo el supuesto de que las mismas son iguales.
Problema Resuelto 3.3. A un estudio en desarrollo de recursos humanos se le pide que determine si los salarios por hora de los ingenieros son los mismos en dos ciudades distintas. Supongamos que se desea probar la hipótesis, a un nivel de significancia de \(0.05\), de que no hay diferencia entre los salarios por hora de los ingenieros, y se asume que los trabajadores no pueden trabajar en las dos ciudades a la vez. Se toma una muestra de trabajadores de cada ciudad y se les consulta el salario por hora medido en dólares, cuyos resultados son los siguientes:
| Salarios medios por hora | Desviación estándar | Tamaño de | |
| de la muestra | poblacional | la muestra | |
| Ciudad 1 | $\(8,95\) | $\(0,40\) | 200 |
| Ciudad 2 | $\(9,10\) | $\(0,60\) | 175 |
Solución
En este problema estamos interesados en conocer si la media de salarios de los ingenieros de dos ciudades distintas son iguales. Si consideramos que las muestras son independientes (un mismo trabajador no puede ser seleccionado en las dos ciudades a la vez), y dado que conocemos las varianzas poblacionales, entonces podemos plantear la siguiente prueba:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \mu_{1}\!=\; & \mu_{2} \nonumber \\ H_{1}\!:\; & \quad \mu_{1}&\neq &\mu_{2} \qquad \textbf{Prueba bilateral} \nonumber \end{aligned}\]
El estadístico de la prueba que usaremos es el de la ecuación [estadistico_m2ic]. \[\begin{aligned} Z_{obs}\!=\; & \frac{(\overline{x}_{1} -\overline{x}_{2})-(\mu_{1}-\mu_{2})}{\sqrt{\sigma_{1}^{2}/n_{1} +\sigma_{2}^{2}/n_{2}}} \nonumber \\ \!=\; & \frac{(8,95-9,10)}{\sqrt{0,40^{2}/200+0,60^{2}/175}}=-2,80 \end{aligned}\]
Debido a que estamos en presencia de una prueba bilateral, vamos a tener dos valores críticos por las zonas de rechazos en ambos lados de la distribución. Además, como el nivel de significancia es del 5%, podemos escribir que:
\[\begin{aligned} \textbf{ZR}=\lbrace Z \in \mathbb{R} \quad \vert \quad Z<Z_{crit1} \vee Z>Z_{crit2} \rbrace \end{aligned}\]
Los valores críticos que determinan la región de rechazo son \(-1,96\) y \(1,96\), entonces:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z<Z_{crit1} \vee Z>Z_{crit2} \rbrace \nonumber \\ \!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z<-1.96 \vee Z>1.96 \rbrace \Rightarrow Z_{obs}=-2.80 \in \textbf{ZR} \end{aligned}\]
En conclusión, se rechaza la hipótesis nula y se concluye que las medias de los salarios por hora de los ingenieros de las dos ciudades no son iguales.
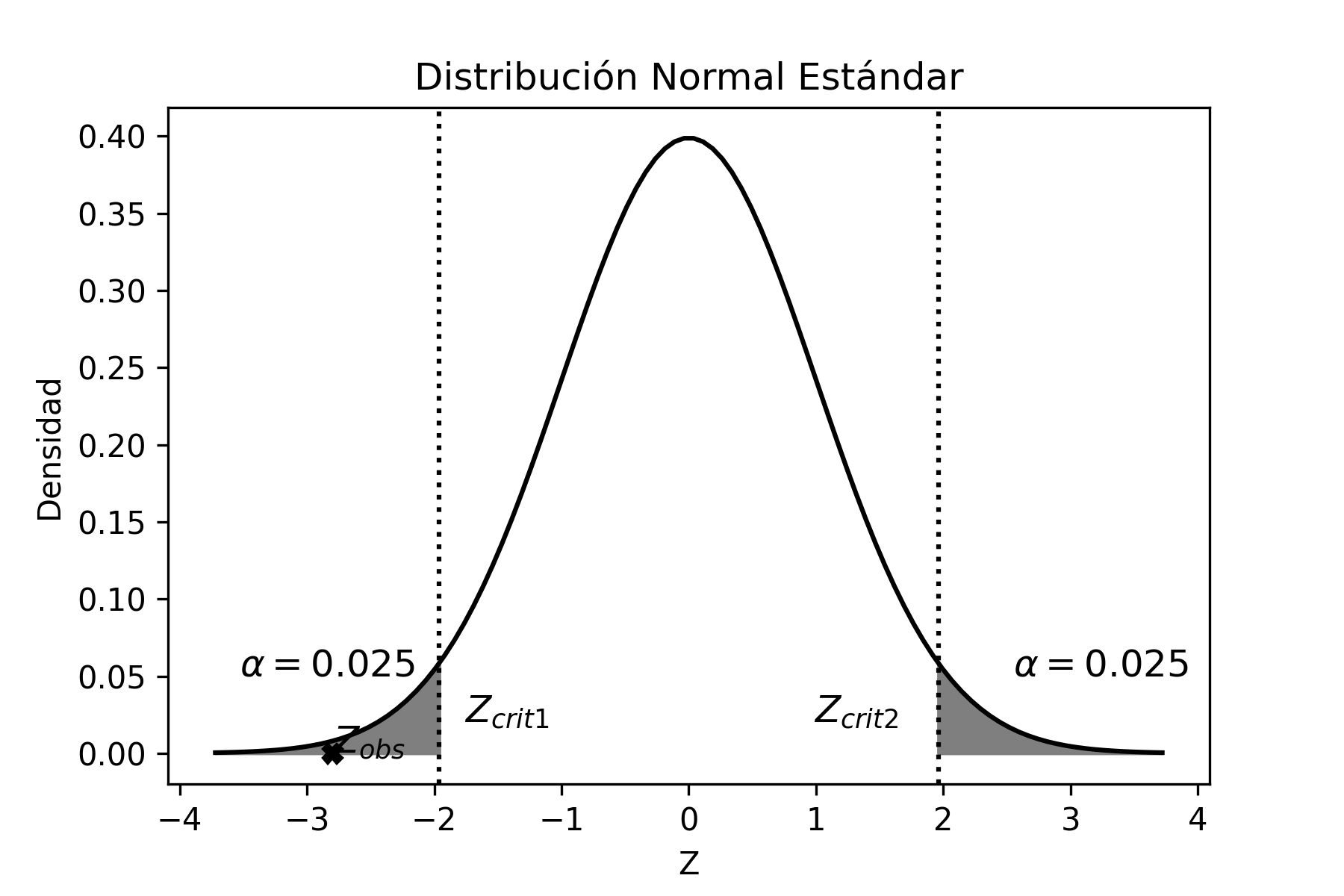
La resolución en Python es:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Diferencia de Medias poblacionales bajo hipotesis nula
dif0=0
# Nivel de significancia
alfa=0.05
# Medias muestrales
x1=8.95
x2=9.10
# Varianza poblacional
var1=0.40**2
var2=0.60**2
# n de cada muestra
n1=200
n2=175
#sides -- 1: dos colas; 2: una cola izquierda; 3: una cola derecha
sides=1
def prueba_z(x1,x2,var1,var2,n1,n2,dif0,alfa,sides):
z_obs = ((x1-x2)-dif0)/(var1/n1+var2/n2)**0.5
if sides==1 and z_obs<0:
p_value = norm.cdf(z_obs)
p_value = 2*p_value
tipo_p="bilateral"
elif sides==1 and z_obs>=0:
p_value = norm.cdf(z_obs)
p_value = 2*(1-p_value)
tipo_p="bilateral"
elif sides==2:
p_value = norm.cdf(z_obs)
p_value = p_value
tipo_p="unilateral izquierda"
elif sides==3:
p_value = norm.cdf(z_obs)
p_value = 1-p_value
tipo_p="unilateral derecha"
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return z_obs,p_value,conclusion,tipo_p
z_obs,p_value,conclusion,tipo_p = prueba_z(x1,x2,var1,var2,n1,n2,dif0,alfa,sides)
print("Prueba de hipotesis", tipo_p)
print("Nivel de significancia =",alfa)
print("Z observado =",z_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis bilateral
Nivel de significancia = 0.05
Z observado = -2.8062430400804628
p valor = 0.005012287145488568
Se rechaza la hipotesis nulaTener en cuenta que, en este caso, en el código no se cargan los valores observados de la muestra, sino que se introducen los estadísticos muestrales, es decir, media, varianza y tamaño de muestra.
Problema Resuelto 3.4. El Departamento de Control de Calidad desea chequear si dos máquinas están produciendo los productos con las mismas especificaciones en relación a su longitud. Para ello tomó muestras aleatorias de tamaño 15 de cada máquina y midió la longitud del producto expresándola en centímetros. El control realizado arrojó los siguientes resultados:
| Máquina | Media muestral | Varianza muestral |
|---|---|---|
| 1 | 149,31 | 2,13 |
| 2 | 150,60 | 1,90 |
¿Podría decir usted que las máquinas están produciendo productos con distinta longitud? Resolver la prueba con un nivel de significancia del 10%.
Solución
Dado que no conocemos las varianzas poblacionales y estamos trabajando con dos muestras independientes, para hacer inferencia sobre la comparación de las medias poblacionales debemos usar el estadístico ([estadistico_m2id]). Es decir la siguiente prueba:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \mu_{1}\!=\; & \mu_{2} \nonumber \\ H_{1}\!:\; & \quad \mu_{1}&\neq &\mu_{2} \qquad \textbf{Prueba bilateral} \nonumber \end{aligned}\]
Estadístico de la prueba \[\begin{aligned} t_{n_{1}+n_{2}-2} ^{obs}\!=\; & \frac{(\overline{x}_{1} -\overline{x}_{2})-(\mu_{1}-\mu_{2})}{s_{p}\sqrt{1/n_{1} +1/n_{2}}} \nonumber \\ \!=\; & \frac{149.31-150.60}{1.42\sqrt{\frac{1}{15}+\frac{1}{15}}}=-2.51 \end{aligned}\] donde \(S_{p}\) viene dado por [sp]:
\[\begin{aligned} s_{p}\!=\; & \sqrt{\frac{(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{(n_{1}-1)+(n_{2}-1)}} \nonumber \\ \!=\; & \sqrt{\frac{(15-1)2.13+(15-1)1.90}{(15-1)+(15-1)}}=\sqrt{2.01}=1.42 \end{aligned}\]
Por lo tanto, la zona de rechazo es:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace t_{n_{1}+n_{2}-2} \in \mathbb{R} \quad \vert \quad t_{n_{1}+n_{2}-2}<t_{n_{1}+n_{2}-2}^{crit1} \vee t_{n_{1}+n_{2}-2}>t_{n_{1}+n_{2}-2}^{crit2} \rbrace \nonumber \\ \!=\; & \lbrace t_{28} \in \mathbb{R} \quad \vert \quad t_{28}<-1.70 \vee t_{28}>1.70 \rbrace \Rightarrow t_{28}^{obs}=-2.51 \in \textbf{ZR} \end{aligned}\]
Como conclusión, a un nivel de significancia del 10%, se rechaza la hipótesis nula de que las medias poblacionales con las que las máquinas fabrican los productos son iguales, en consecuencia, las máquinas producen con distinta longitud media los productos.
Gráficamente se tiene:
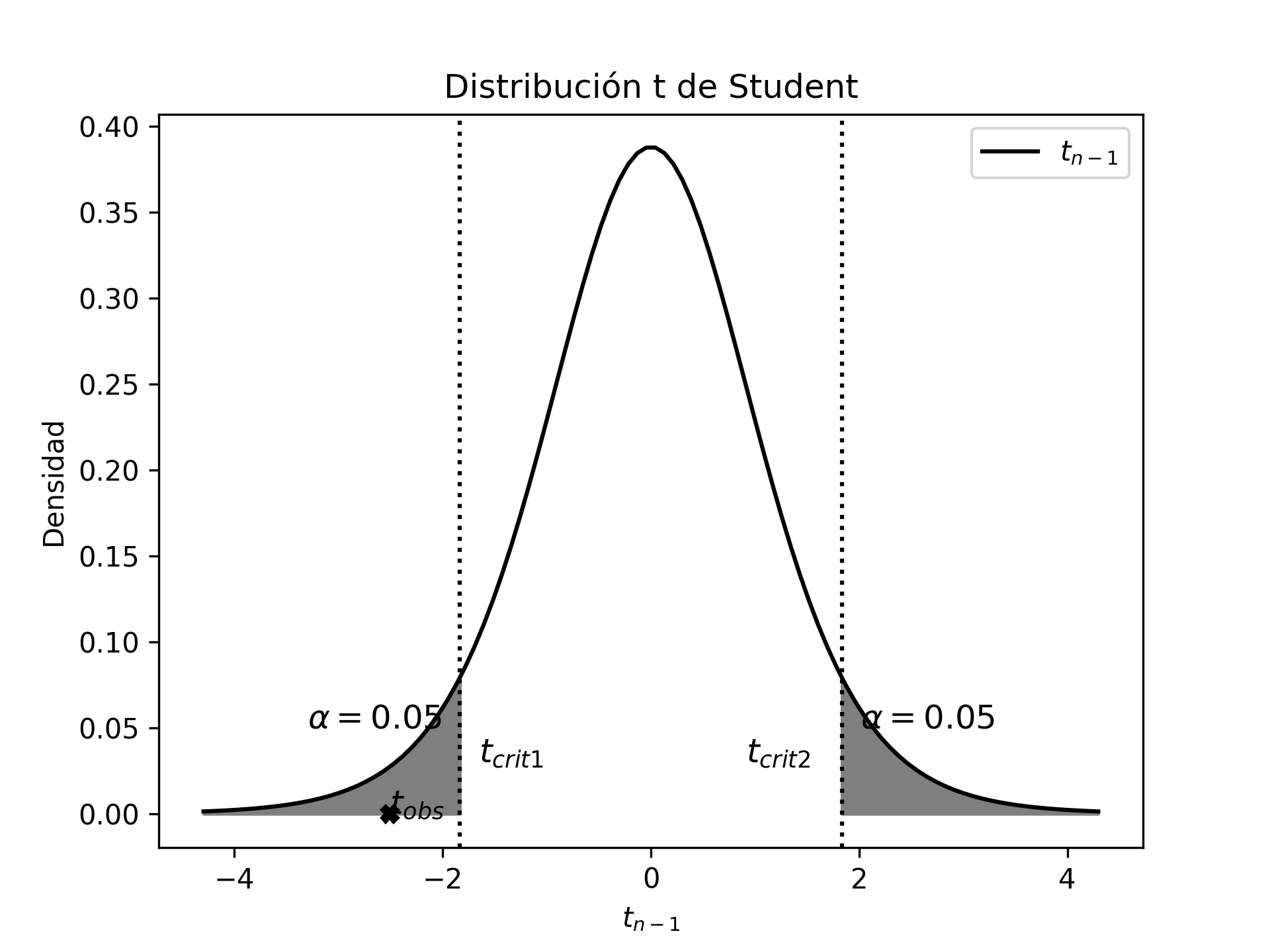
La resolución del ejercicio en Python es la que sigue:
# Librerias
from scipy import stats
import numpy as np
import statistics
from statistics import stdev
# Nivel de significancia
alfa=0.10
# Diferencia de medias bajo H0
du0=0
# Datos muestrales
data1=[151.49,146.06,152.30,149.61,149.55,150.12,147.74,148.43,
149.59,148.50,149.85,149.29,148.85,148.78,149.41]
data2=[152.67,147.55,153.43,150.89,150.83,151.38,149.13,149.78,
150.87,149.84,151.12,150.60,150.17,150.11,150.70]
#sides -- 1: dos colas; 2: una cola izquierda; 3: una cola derecha
sides=1
def prueba_t(data1,data2,du0,alfa,sides):
n1=len(data1)
data1_mean = np.mean(data1)
data1_sd = stdev( data1, data1_mean )
n2=len(data2)
data2_mean = np.mean(data2)
data2_sd = stdev( data2, data2_mean )
sp=((n1-1)*data1_sd**2+(n2-1)*data2_sd**2)/(n1+n2-2)
t_obs = ((data1_mean-data2_mean)-du0)/(sp*(1/n1+1/n2))**0.5
t = stats.t(n1+n2-2)
if sides==1 and t_obs<0:
p_value = t.cdf(t_obs)
p_value = 2*p_value
tipo_p="bilateral"
elif sides==1 and t_obs>=0:
p_value = t.cdf(t_obs)
p_value = 2*(1-p_value)
tipo_p="bilateral"
elif sides==2:
p_value = t.cdf(t_obs)
p_value = p_value
tipo_p="unilateral izquierda"
elif sides==3:
p_value = t.cdf(t_obs)
p_value = 1-p_value
tipo_p="unilateral derecha"
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return t_obs,p_value,conclusion,n1,n2,data1_mean,data1_sd,data2_mean,data2_sd,tipo_p,sp
t_obs,p_value,conclusion,n1,n2,data1_mean,data1_sd,data2_mean,data2_sd,tipo_p,sp = prueba_t(data1,data2,du0,alfa,sides)
print("Prueba de hipotesis", tipo_p)
print("Media Muestral 1 =",data1_mean)
print("Media Muestral 2 =",data2_mean)
print("S Muestral 1 =",data1_sd)
print("S Muestral 2 =",data2_sd)
print("n1 =",n1)
print("n2 =",n2)
print("Nivel de significancia =",alfa)
print("t observado =",t_obs)
print("p valor = ",p_value/sides)
# Conclusion de la prueba de hipotesis
if p_value/sides < alfa:
print("Se rechaza la hipotesis nula")
else:
print("No se rechaza la hipotesis nula")
Prueba de hipotesis bilateral
Media Muestral 1 = 149.30466666666663
Media Muestral 2 = 150.60466666666665
S Muestral 1 = 1.4596127992757288
S Muestral 2 = 1.3766048642878415
n1 = 15
n2 = 15
Nivel de significancia = 0.1
t observado = -2.509449735971287
p valor = 0.018152489240377594
Se rechaza la hipotesis nulaTener en cuenta que, en este caso, es necesario cargar los valores muestrales observados en el código.
Muestras dependientes
Supongamos que queremos estudiar un grupo de individuos a los cuales se le ha realizado un tratamiento (puede ser una capacitación, un entrenamiento, etc) y que, para evaluar el impacto que el mismo ha tenido efectuamos, por cada individuo (que denominaremos unidad experimental), dos mediciones de la variable respuesta: una antes y la otra después del tratamiento. La variable respuesta podría ser: cantidad producida, aumento de la productividad, puntaje obtenido en una evaluación de aprendizaje, etc. En este caso estamos ante la presencia de dos muestras dependientes7, ya que a las mismas unidades experimentales se las mide en distintos momentos temporales.
Entonces, sean \(X_{1}\) y \(X_{2}\) las variables de respuesta asociadas a los dos momentos del tiempo, cuyas medias son \(\mu_{1}\) y \(\mu_{2}\) respectivamente, con tamaños de muestras iguales a \(n\). Si tomamos diferencias de dichas variables aleatorias, y dado que tenemos un único tamaño de muestra correspondiente a mediciones de la misma unidad experimental, entonces los efectos intrínsecos propios del individuo (por ejemplo sexo de la persona, coeficiente intelectual, nacionalidad, etc) desaparecen, y nos queda el efecto del tratamiento sobre dicha unidad experimental. Por lo tanto podemos denotar por \(\delta=X_{1}-X_{2}\) a la nueva variable en la población y \(d\) a dicha variable en la muestra, con lo cual, por el TCL:
\[{ \frac{\overline{d}-(\mu_{2}-\mu_{1})}{\sigma_{\delta}/\sqrt{n}} \sim N(0,1)}\] que es el estadístico para esta prueba de diferencia de medias con muestras dependientes.
En caso de no conocer \(\sigma_{\delta}\), se utiliza:
\[\begin{aligned} S_{d}=\frac{\sum_{i=1}^{n}(d_{i}-\overline{d})^{2}}{n-1} \end{aligned}\] donde \(d_{i}=X_{1i}-X_{2i}\), por lo tanto se llega a: \[\label{estadistico_m2d} { \frac{\overline{d}-(\mu_{2}-\mu_{1})}{S_{d}/\sqrt{n}} \sim t_{n-1}}\] equivalente al estadístico \(t\) para la prueba de medias de una muestra.
La gran ventaja de hacer la transformación \(\delta=X_{1}-X_{2}\) es que todos los inobservables propios de los individuos desaparecen, y sólo queda el impacto del tratamiento8.
Problema Resuelto 3.5. Existe un programa de reducción de peso en el que se afirma que, el participante promedio del programa pierde más de 15 kilos. Se toma una muestra de 10 participantes y se anota el peso antes y después del programa.
| Peso en kg | ||
|---|---|---|
| Antes | Después | Pérdida |
| 90 | 78 | 12 |
| 95 | 85 | 10 |
| 88 | 73 | 15 |
| 101 | 88 | 13 |
| 99 | 89 | 10 |
| 109 | 89 | 20 |
| 94 | 83 | 11 |
| 97 | 85 | 12 |
| 104 | 90 | 14 |
| 110 | 97 | 13 |
¿Es correcta la afirmación que realiza el programa de reducción de peso? Se exige un nivel de significancia de \(0.05\).
Solución
Este programa de reducción de peso puede ser considerado como un tratamiento que se hace a los participantes, en donde medimos la variable respuesta (el peso del participante) en dos momentos del tiempo, antes del inicio del programa (pre-tratamiento) y después de finalizado (post-tratamiento). Por lo tanto, el estadístico de esta prueba es el que viene dado por la expresión ([estadistico_m2d]) ya que no conocemos el valor de \(\sigma_{D}\), y la prueba de hipótesis se plantea de la siguiente manera:
\[\begin{aligned} H_{0}\!:\; & \quad (\mu_{2}-\mu_{1}) &\leq& 15 \quad \text{kilos} \nonumber \\ H_{1}\!:\; & \quad (\mu_{2}-\mu_{1}) &>&15 \quad \text{kilos} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
\[\begin{aligned} t_{n-1}^{obs}\!=\; & \frac{\overline{d}-(\mu_{2}-\mu_{1})_{0}} {S_{{d}}/ \sqrt{n}} \end{aligned}\]
Calculando los valores correspondientes a \(\overline{d}\) y \(S_{d}\):
| Peso en kg | |||
|---|---|---|---|
| Antes | Después | Pérdida | |
| \(x_{1}\) | \(x_{2}\) | \(d=x_{1}-x_{2}\) | |
| 90 | 78 | 12 | |
| 95 | 85 | 10 | |
| 88 | 73 | 15 | |
| 101 | 88 | 13 | |
| 99 | 89 | 10 | |
| 109 | 89 | 20 | |
| 94 | 83 | 11 | |
| 97 | 85 | 12 | |
| 104 | 90 | 14 | |
| 110 | 97 | 13 | |
| Media | 98.70 | 85.70 | 13.00 |
| \(S\) | 7.42 | 6.68 | 2.94 |
Luego, reemplazando dichos valores para calcular el estadístico observado de la prueba, tenemos: \[\begin{aligned} t_{n-1}^{obs}\!=\; & \frac{\overline{d}-(\mu_{2}-\mu_{1})_{0}} {s_{d}/ \sqrt{n}} \nonumber \\ \!=\; & \frac{13,0-15}{2,94/\sqrt{10}}=-2,14 \end{aligned}\]
En notación de conjuntos, y teniendo en cuenta que los grados de libertad son \(n-1=9\), tenemos que la zona de rechazo viene dada por: \[\begin{aligned} \textbf{ZR}\!=\; & \lbrace t_{n-1} \in \mathbb{R} \quad \vert \quad t_{n-1}>t_{n-1}^{crit2} \rbrace \nonumber \\ \!=\; & \lbrace t_{9} \in \mathbb{R} \quad \vert \quad t_{9}>1.83 \rbrace \Rightarrow t_{9}^{obs}=-2.14 \notin \textbf{ZR} \end{aligned}\]
Con lo cual, no se rechaza la hipótesis nula a un nivel de significancia del 5%, en consecuencia no hay evidencia suficiente para afirmar que el programa reduce el peso del participante en, al menos, 15 kilos.
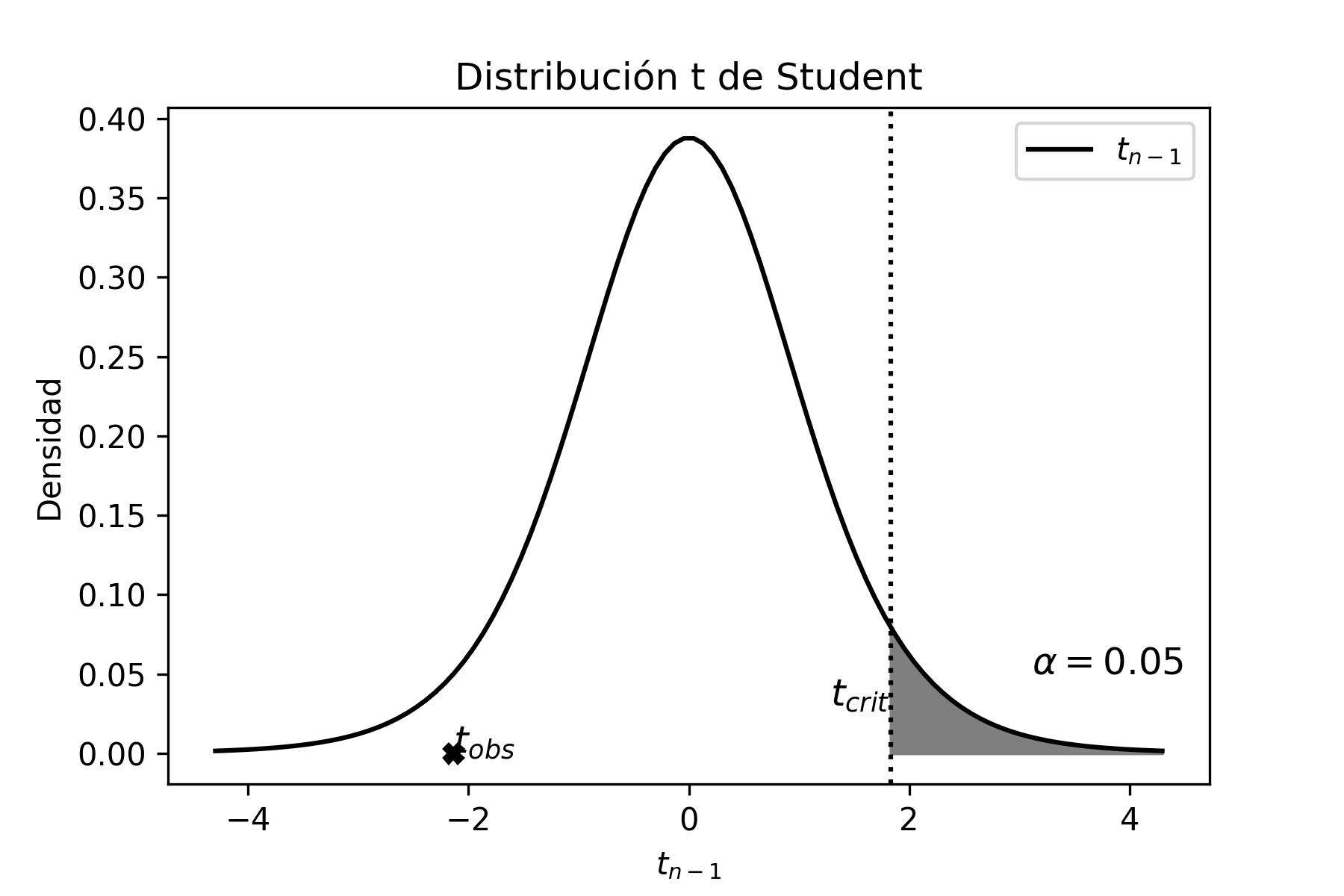
La resolución utilizando Python es muy similar al caso de una prueba t con una muestra (ver página ), pero ahora nuestra variable de análisis es la diferencia de las mediciones entre “Antes” y “Después” del tratamiento.
# Librerias
from scipy.stats import ttest_1samp
import numpy as np
import statistics
from statistics import stdev
# Diferencia de media bajo hipotesis nula
d0=15
# Nivel de significancia
alfa=0.05
# Datos muestrales
data1=[90,95,88,101,99,109,94,97,104,110]
data2=[78,85,73,88,89,89,83,85,90,97]
data=list(np.array(data1) - np.array(data2))
#sides -- 1: dos colas; 2: una cola izquierda 3: una cola derecha
sides=3
if sides==1:
colas=2
else:
colas=1
n1=len(data1)
data1_mean = np.mean(data1)
data1_sd = stdev( data1, data1_mean )
n2=len(data2)
data2_mean = np.mean(data2)
data2_sd = stdev( data2, data2_mean )
tset, p_value = ttest_1samp(data, d0)
if sides==1 or sides==2:
p_value=p_value/sides
else:
p_value=1-p_value/(sides-1)
print("Prueba de hipotesis de ",colas," cola.")
print("Media Muestral 1 =",data1_mean)
print("Media Muestral 2 =",data2_mean)
print("S Muestral 1 =",data1_sd)
print("S Muestral 2 =",data2_sd)
print("n 1 =",n1)
print("n 2 =",n2)
print("Nivel de significancia =",alfa)
print("t observado =",tset)
print("p valor = ",p_value)
# Conclusion de la prueba de hipotesis
if p_value < alfa:
print("Se rechaza la hipotesis nula")
else:
print("No se rechaza la hipotesis nula")
Prueba de hipotesis de 1 cola.
Media Muestral 1 = 98.7
Media Muestral 2 = 85.7
S Muestral 1 = 7.4244341348160825
S Muestral 2 = 6.684143758012524
n 1 = 10
n 2 = 10
Nivel de significancia = 0.05
t observado = -2.1483446221182985
p valor = 0.9699007170884624
No se rechaza la hipotesis nulaDado que estamos en un caso de dos muestras dependientes, los vectores de datos de entrada tienen que tener la misma dimensión, caso contrario el comando que calcula la prueba nos devolverá un error.
Pruebas para la Proporción Poblacional
Para las pruebas de hipótesis sobre la proporción poblacional, diferenciaremos entre una muestra y dos muestras independientes. El resto de casos queda fuera del análisis de este libro.
Prueba para la Proporción de una Población
Por el TCL sabemos que:
\[\label{estadistico_p2} { \frac{P-\pi}{\sqrt{\pi(1-\pi)/n}} \sim N(0,1)}\] donde \(n\) tiene que ser lo suficientemente grande y se deben satisfacer las condiciones del Teorema de De Moivre - Laplace (ver página ) para que la aproximación del estadístico pueda ser utilizada.
Problema Resuelto 3.6. La Facultad de una determinada Universidad afirma que el 85% de los estudiantes está de acuerdo con el pago de una contribución estudiantil, mientras que el Centro de Estudiantes de esa Facultad sostiene que el porcentaje es bastante menor. En busca de evidencia en la afirmación del Centro de Estudiantes, se toma una muestra aleatoria de 160 alumnos de distintos niveles de cursado y se consulta si están a favor o no de la contribución estudiantil. Como resultado se obtienen 130 casos a favor de dicha contribución. ¿Puede ayudar al Centro de Estudiantes a justificar su opinión con un nivel de significancia del 5%?
Solución
En este problema estamos interesados en conocer la proporción poblacional, por lo que se debe utilizar el estadístico ([estadistico_p2]), siempre y cuando se cumplan las condiciones de aproximación del mismo. Además, dado que se quiere demostrar que la opinión del Centro de Estudiantes es correcta, formulamos la prueba como sigue:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \pi &\geq& 0.85 \nonumber \\ H_{1}\!:\; & \quad \pi &<& 0.85 \qquad \textbf{Prueba lateral izquierda} \nonumber \end{aligned}\]
Verifiquemos las condiciones de aproximación, sabiendo que la proporción muestral viene dada por \(p=130/160=0.813\)
\[\begin{aligned} n\cdot p\!=\; & 160 \cdot 0.813 = 136 > 5 \nonumber \\ n(1-p) \!=\; & 160 \cdot (1- 0.813) = 24 > 5 \end{aligned}\]
Como que se cumplen los supuestos, podemos escribir:
\[\begin{aligned} Z_{obs}\!=\; & \frac{p-\pi_{0}}{\sqrt{\pi_{0}(1-\pi_{0})/n}} \nonumber \\ \!=\; & \frac{0.813-0.85}{\sqrt{0.85(1-0.85)/160}} \nonumber \\ \!=\; & -1.33 \end{aligned}\]
Sabiendo que la prueba es unilateral izquierda y con un \(\alpha=0.05\), entonces el \(Z_{crit}=-1.64\). En consecuencia, tenemos que:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z<Z_{crit} \rbrace \nonumber \\ \!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z<-1.64\rbrace \Rightarrow Z_{obs}=-1.33 \notin \textbf{ZR} \end{aligned}\]
En este caso es \(Z_{obs}=-1.33\), por lo que no se rechaza \(H_{0}\), ya que no hay evidencia suficiente, al nivel de significancia del 5%, para afirmar que la opinión del Centro de Estudiantes es correcta.
La representación gráfica es:
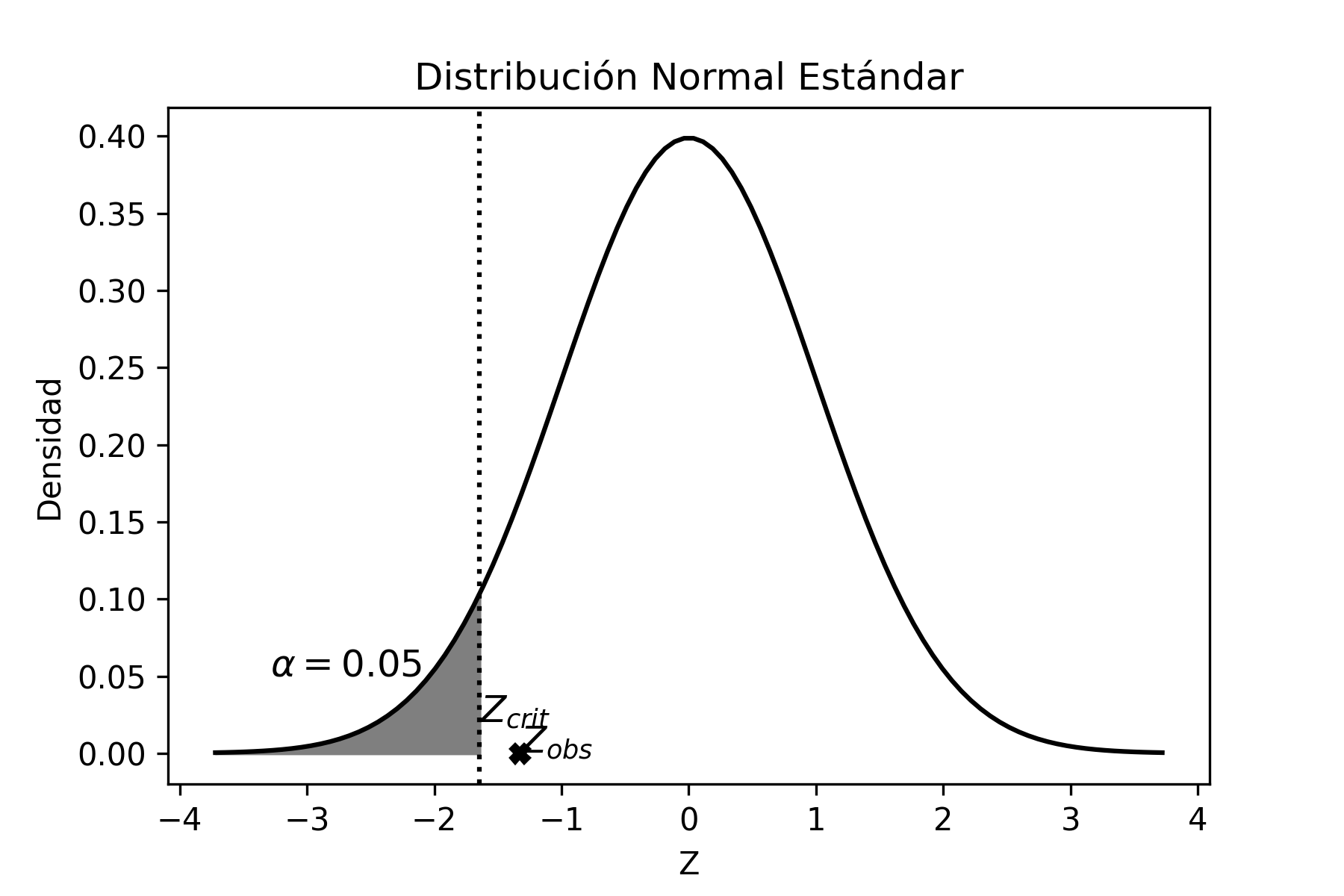
La resolución en Python es:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Proporcion bajo hipotesis nula (valor entre 0 y 1)
P0=0.85
# Nivel de significancia
alfa=0.05
# Casos favorables (valor entero menor o igual a n)
X=130
# n de la muestra
n=160
#sides -- 1: una cola; 2: dos colas
sides=2
def prueba_z(X,n,P0,alfa,sides):
P=X/n
z_obs = (P-P0)/(P0*(1-P0)/n)**0.5
p_value = norm.sf(abs(z_obs))*sides
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return z_obs,p_value,conclusion,P
z_obs,p_value,conclusion,P = prueba_z(X,n,P0,alfa,sides)
print("Prueba de hipotesis de ",sides," cola.")
print("Nivel de significancia =",alfa)
print("Proporcion muestral =",P)
print("Z observado =",z_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis de 2 cola.
Nivel de significancia = 0.05
Proporcion muestral = 0.8125
Z observado = -1.3284223283101422
p valor = 0.1840386271964256
No se rechaza la hipotesis nulaPrueba para la Diferencia de dos Proporciones Poblacionales
Supongamos que tenemos dos variables aleatorias independientes que se distribuyen de la siguiente forma:
\[\begin{aligned} P_{1} \sim N \bigg( \pi_{1},\pi_{1}(1-\pi_{1})/n \bigg) \nonumber \\ P_{2} \sim N \bigg( \pi_{2},\pi_{2}(1-\pi_{2})/n \bigg) \end{aligned}\]
Restando ambas variables y estandarizando,
\[\begin{aligned} \frac{(P_{1}-P_{2})-(\pi_{1}-\pi_{2})}{\sqrt{\frac{\pi_{1}(1-\pi_{1})}{n_{1}}+\frac{\pi_{2}(1-\pi_{2})}{n_{2}}}} \sim N(0,1) \end{aligned}\]
Bajo la hipótesis nula verdadera (o sea \(\pi_{1}=\pi_{2}=\pi\)), la ecuación anterior se convierte en:
\[\begin{aligned} \frac{(P_{1}-P_{2}) }{\sqrt{\frac{\pi(1-\pi)}{n_{1}}+\frac{\pi(1-\pi)}{n_{2}}}} \sim N(0,1) \nonumber \\ \frac{(P_{1}-P_{2})}{\sqrt{\pi(1-\pi)\bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}}\bigg)}} \sim N(0,1) \end{aligned}\]
Como \(\pi\) no se conoce, se combinan las estimaciones puntuales de las dos muestras para así obtener un solo estimador puntual de \(\pi\), que simbolizamos por \(P_{a}\). Es decir:
\[\begin{aligned} \label{p_amalgamada} P_{a}=\frac{n_{1}P_{1}+n_{2}P_{2}}{n_{1}+n_{2}} \end{aligned}\]
A esta proporción se la conoce como \(P\) amalgamado. En consecuencia, el estadístico para diferencia de proporciones independientes viene dado por:
\[\label{estadistico_p2a} { \frac{(P_{1}-P_{2}) }{\sqrt{P_{a}(1-P_{a})\bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}}\bigg)}} \sim N(0,1)}\]
Problema Resuelto 3.7. El Gerente de Control de Calidad de una fábrica de partes de automóviles, que posee dos terminales distintas (1 y 2), debe informar si la proporción de partes defectuosas producidas en la terminal 1 es mayor a la producida en la terminal 2. Para ello, se extraen muestras aleatorias de 100 partes fabricadas en cada una de las terminales, obteniéndose los siguientes resultados:
| Terminal 1 | Terminal 2 | |
|---|---|---|
| Partes Defectuosas | 25 | 12 |
| Partes No Defectuosos | 75 | 88 |
Con un nivel de significancia del 5%, ¿a qué conclusión llega el Gerente?
Solución
Aquí estamos en presencia de una prueba sobre la diferencia de proporciones de defectuosos entre dos muestras, una de la terminal 1 y otra de la terminal 2. Entonces, podemos plantear las siguientes hipótesis:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \pi_{1} &\leq& \pi_{2} \nonumber \\ H_{1}\!:\; & \quad \pi_{1} &>& \pi_{2} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Para esta prueba, se debe usar el estadístico de la ecuación [estadistico_p2a], siempre que se verifiquen los supuestos de que \(n_{i}p_{i}>5\) (Teorema de De Moivre - Laplace), es decir:
\[\begin{aligned} n_{1}p_{1}\!=\; & 100 \cdot \frac{25}{100}=25>5 \nonumber \\ n_{1}(1-p_{1})\!=\; & 100 (1-\frac{25}{100})=75>5 \nonumber \\ n_{2}p_{2}\!=\; & 100 \cdot \frac{12}{100}=12>5 \nonumber \\ n_{2}(1-p_{2})\!=\; & 100 (1-\frac{12}{100})=88>5 \end{aligned}\]
Sabiendo que se satisfacen los supuestos, entonces aplicamos ([p_amalgamada]) para obtener \(P_{a}=0.185\) y luego calcular el estadístico de la prueba.
\[\begin{aligned} Z_{obs}\!=\; & \frac{(p_{1}-p_{2})} {\sqrt{p_{a}(1-p_{a})\bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}}\bigg)}} \nonumber \\ \!=\; & \frac{(0.25-0.12)}{\sqrt{0.185(1-0.185)\bigg(\frac{1}{100}+\frac{1}{100}\bigg)}}=2.37 \end{aligned}\]
Determinamos la zona de rechazo como:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z>Z_{crit} \rbrace \nonumber \\ \!=\; & \lbrace Z \in \mathbb{R} \quad \vert \quad Z>1.64\rbrace \Rightarrow Z_{obs}=2.37 \in \textbf{ZR} \end{aligned}\]
En conclusión, rechazamos la hipótesis nula y por lo tanto, la proporción de defectuosos de la terminal 1 es superior a la de la terminal 2, con un nivel de significancia del 5%. Gráficamente, tenemos:
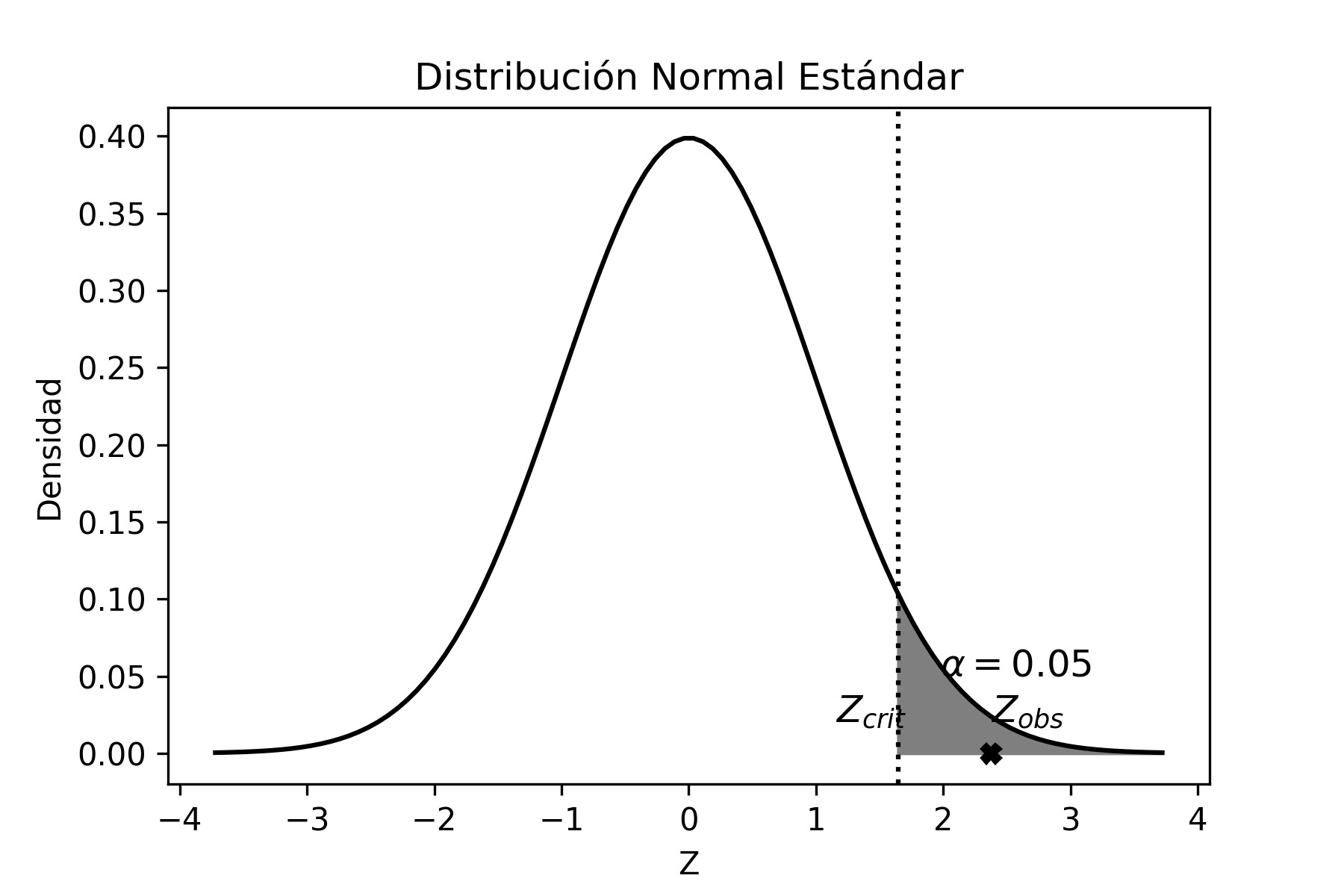
El código en este caso es similar al ejemplo anterior, en donde teníamos una sola muestra. Haciendo pequeñas modificaciones tenemos:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import norm
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Diferencia de Proporciones bajo hipotesis nula (valor entre -1 y 1)
difP0=0
# Nivel de significancia
alfa=0.05
# Casos favorables (valor entero menor o igual a n)
X1=25
X2=12
# n de las muestras
n1=100
n2=100
#sides -- 1: una cola; 2: dos colas
sides=2
def prueba_z(X1,X2,n1,n2,P0,alfa,sides):
P1=X1/n1
P2=X2/n2
Pa=(n1*P1+n2*P2)/(n1+n2)
z_obs = ((P1-P2)-difP0)/(Pa*(1-Pa)*(1/n1+1/n2))**0.5
p_value = norm.sf(abs(z_obs))*sides
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return z_obs,p_value,conclusion
z_obs,p_value,conclusion = prueba_z(X1,X2,n1,n2,P0,alfa,sides)
print("Prueba de hipotesis de ",sides," cola.")
print("Nivel de significancia =",alfa)
print("Z observado =",z_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis de 2 cola.
Nivel de significancia = 0.05
Z observado = 2.367356623645556
p valor = 0.01791566018303965
Se rechaza la hipotesis nulaPruebas para la Varianza Poblacional
Para pruebas sobre la varianza poblacional, distinguiremos entre una población y dos poblaciones.
Prueba para la Varianza de una Población
Cuando estamos interesados en aplicar una prueba de hipótesis sobre la varianza poblacional, se hace uso del estadístico \(\chi^{2}\) según ([estadistico_chi]).
\[{\chi^{2}_{n-1}=\frac{(n-1)S^{2}}{\sigma^{2}}}\]
Problema Resuelto 3.8. Un fabricante de cemento afirma que su producto tiene una resistencia, medida en kilogramos por centímetro cuadrado, relativamente estable y baja, cuyo recorrido es de \(\sigma=10\) kg/cm\(^{2}\) alrededor del valor medio. Sin embargo, un cliente contradice al fabricante y asegura que no se cumple con la especificación informada del producto. Para poder responder a la inquietud del cliente, se toma una muestra aleatoria de \(n=10\) observaciones donde se obtiene una media \(\overline{x}=312\) y una varianza \(S^{2}=195\). ¿Qué podría decir el fabricante acerca de la afirmación del cliente? Suponer que la población de la variable se distribuye normalmente. Se decide trabajar con \(\alpha=0.05\).
Solución
Cuando el parámetro poblacional de interés es la varianza, el estadístico que se usa es \(\chi^{2}\), bajo el supuesto de población normal. Como el fabricante dice que la resistencia es relativamente baja y estable, vamos a plantear la hipótesis nula desde el punto de vista del cliente, entonces:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \sigma^{2}&\leq &10^{2} \nonumber \\ H_{1}\!:\; & \quad \sigma^{2}&>&10^{2} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Y el estadístico de la prueba es:
\[\begin{aligned} \chi^{2}_{obs}\!=\; & \frac{(n-1)s^{2}}{\sigma^{2}} \nonumber \\ \!=\; & \frac{\left( 10-1 \right) 195} {10^2}=17.55 \end{aligned}\]
La zona de rechazo de \(H_{0}\) es:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace \chi^{2}_{n-1} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{n-1}>\chi^{2}_{crit} \rbrace \nonumber \\ \!=\; & \lbrace \chi^{2}_{9} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{9}>16.92\rbrace \Rightarrow \chi^{2}_{obs}=17.55 \in \textbf{ZR} \end{aligned}\]
El valor de \(\chi^{2}_{crit}\) para un nivel de significancia de 5% y 9 grados de libertad es \(16,92\), entonces el estadístico cae en la zona de rechazo de la hipótesis nula. En conclusión, el cliente está en lo cierto, y el fabricante no está cumpliendo con los requisitos al existir evidencia de que la resistencia del cemento tiene una variabilidad mayor a la reportada.
Gráficamente tenemos:
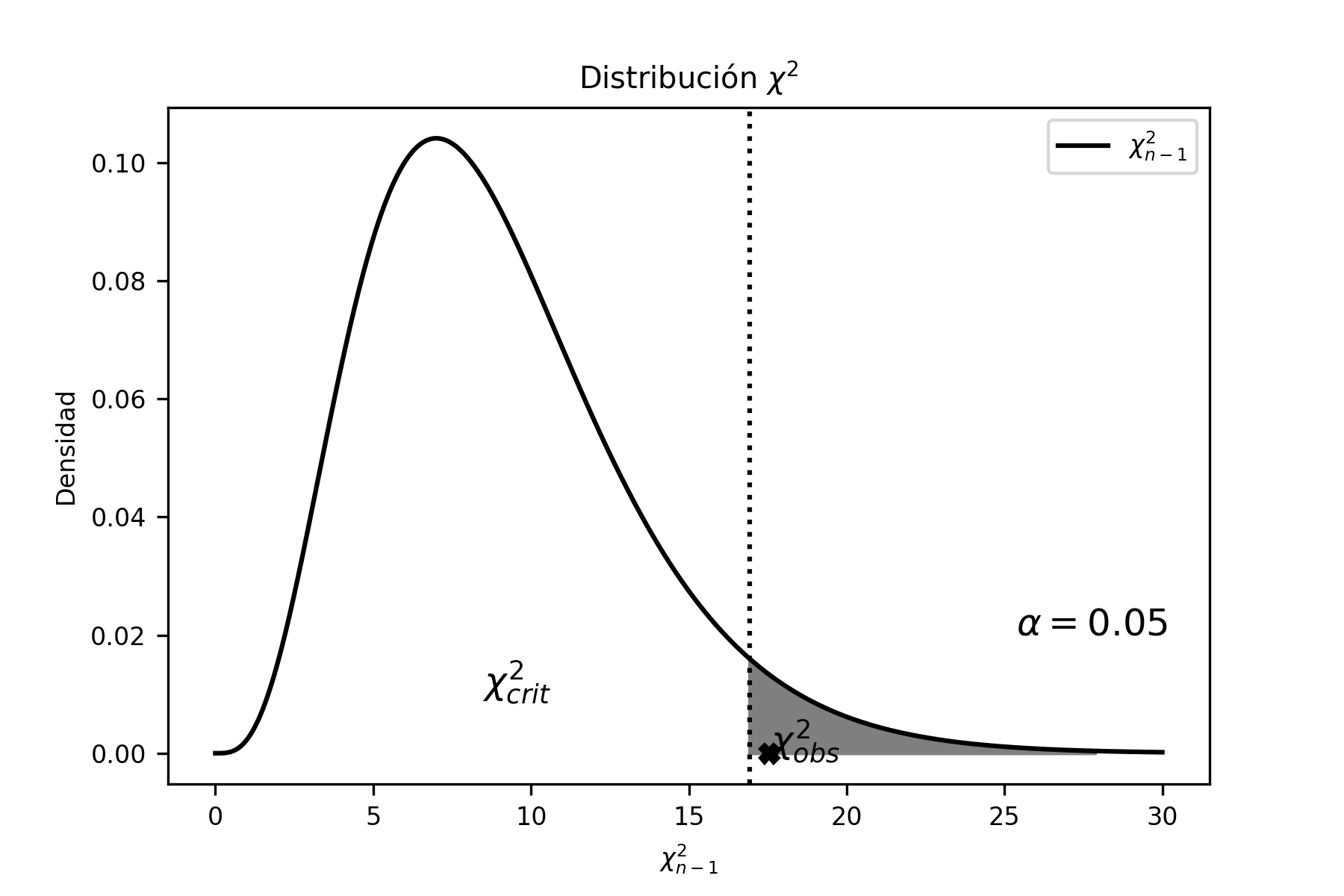
Realizando la prueba de hipótesis con Python, llegamos al siguiente script:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import chi2
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Varianza poblacional bajo hipotesis nula
var0=10**2
# Nivel de significancia
alfa=0.05
# Datos muestrales
data=[293.91,305.70,315.47,321.10,302.15,326.82,281.47,299.19,305.10,320.38]
#sides -- 1: una cola; 2: dos colas
sides=1
def prueba_chi(data,alfa,sides):
n = len(data)
data_mean = np.mean(data)
data_sd = stdev( data, data_mean )
chi_obs = ((n-1)*data_sd**2)/var0
p_value = chi2.sf(chi_obs,n-1)*sides
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return chi_obs,p_value,conclusion,data_sd
chi_obs,p_value,conclusion,data_sd = prueba_chi(data,alfa,sides)
print("Prueba de hipotesis de ",sides," cola.")
print("Nivel de significancia =",alfa)
print("Chi2 observado =",chi_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis de 1 cola.
Nivel de significancia = 0.05
Chi2 observado = 17.551888899999984
p valor = 0.04074305047051333
Se rechaza la hipotesis nulaPrueba para Comparación de Varianzas de dos Poblaciones
En el caso de trabajar con dos poblaciones y estar interesados en comparar las varianzas poblacionales, se usa el estadístico \(F\) (ecuación [estadistico_f1]), es decir:
\[\begin{aligned} F_{n_{1}-1,n_{2}-1}=\frac{\frac{U}{n_{1}-1}}{\frac{V}{n_{2}-1}}=\frac{ \frac{\frac{(n_{1}-1)S_{1}^{2}}{\sigma_{1}^{2}}}{n_{1}-1}} {\frac{\frac{(n_{2}-1)S_{2}^{2}}{\sigma_{2}^{2}}}{n_{2}-1}}=\frac{S_{1}^{2}}{S_{2}^{2}}\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} \end{aligned}\]
Bajo la hipótesis nula verdadera (\(\sigma_{1}=\sigma_{2}\)), el estadístico \(F\) toma la forma:
\[{ F_{n_{1}-1,n_{2}-1}=\frac{S_{1}^{2}}{S_{2}^{2}}}\]
Este estadístico es válido cuando las poblaciones son normales e independientes.
Problema Resuelto 3.9. Se sabe que las calificaciones promedio obtenidas por los alumnos de una universidad que usa plataforma virtual de enseñanza en una materia fue, aproximadamente, la misma en el turno mañana que en el turno tarde. Sin embargo, existe sospecha que el turno tarde presenta mayor variabilidad, por lo que se toma una muestra de calificaciones de cada turno que arrojó los resultados que se presentan en la siguiente tabla:
| Turno | \(n\) | Media Muestral | Varianza Muestral |
| Mañana | 53 | 6,41 | 2,15 |
| Tarde | 50 | 6,23 | 2,36 |
¿Se podría decir que el turno tarde tuvo mayor variabilidad de notas en relación al turno de la mañana a un nivel de significancia del 5%? Suponer normalidad en las poblaciones de las variables.
Solución
Cuando estamos analizando la variabilidad de una variable, nos estamos refiriendo a la varianza de la misma. Además, dado que queremos analizar el turno tarde y el turno mañana, tenemos dos poblaciones, las cuales se suponen que se distribuyen normal. Como se quiere demostrar que el turno tarde tiene mayor variabilidad que el de la mañana, entonces podemos escribir las hipótesis de la siguiente forma:
Planteo de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \sigma_{1:\text{tarde}}^{2}&\leq &\sigma_{2:\text{mañana}}^{2} \nonumber \\ H_{1}\!:\; & \quad \sigma_{1:\text{tarde}}^{2}&>& \sigma_{2:\text{mañana}}^{2} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Donde el estadístico de prueba es \(F\), es decir:
\[\begin{aligned} F^{obs}\!=\; & \frac{s_{1}^{2}}{s_{2}^{2}} \nonumber \\ \!=\; & \frac{2.36}{2.15}=1.11 \end{aligned}\]
Considerando los grados de libertad \((n_{1}-1)=52\), y \((n_{2}-1)=49\) para el numerador y el denominador respectivamente, tenemos que el punto crítico es \(F_{52,49}^{crit}=1.59\) con un \(\alpha=0.05\). Con lo cual:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace F_{n_{1}-1,n_{2}-1} \in \mathbb{R} > 0 \quad \vert \quad F_{n_{1}-1,n_{2}-1}>F_{n_{1}-1,n_{2}-1}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace F_{52,49} \in \mathbb{R} > 0 \quad \vert \quad F_{52,49}>1.59\rbrace \Rightarrow F^{obs}=1.11 \notin \textbf{ZR} \end{aligned}\]
En consecuencia, el \(F^{obs}\) cae en zona de no rechazo de la \(H_{0}\), por lo que no hay evidencia suficiente para aseverar que la variabilidad de las notas del turno tarde es mayor que la del turno mañana.
Gráficamente es:
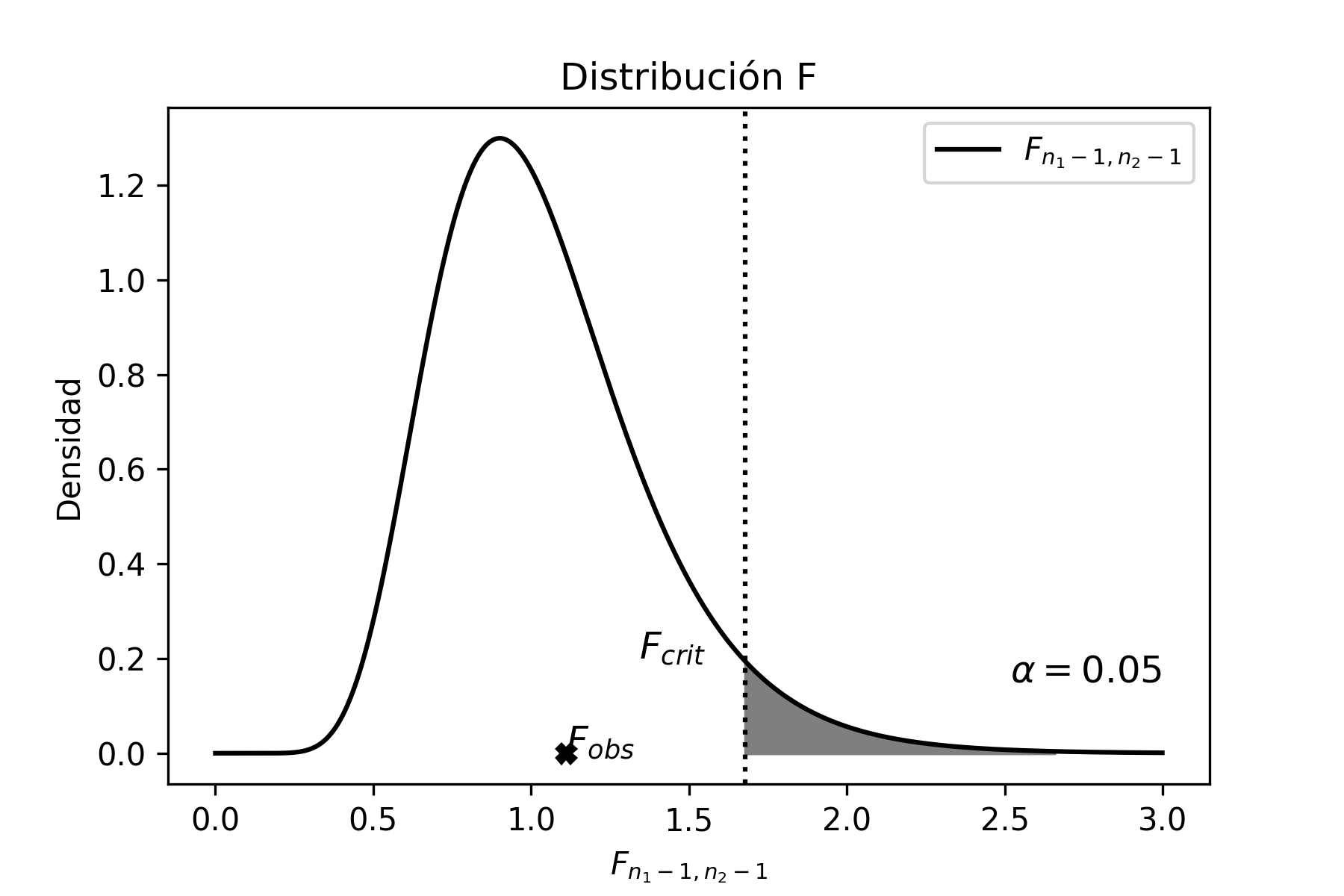
Resolviendo en Python escribimos el siguiente programa:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import f
from statsmodels.stats import weightstats as stests
import statistics
from statistics import stdev
# Nivel de significancia
alfa=0.05
# Datos muestrales
data1=[7.34,3.94,7.11,5.28,6.23,8.33,5.27,7.66,8.25,7.49,5.84,
7.27,6.74,7.04,6.75,4.89,6.49,6.67,8.5,6.08,4.3,5.01,5.74,
3.8,5.58,4.84,7.42,9.3,7.37,8.44,7.33,8.65,5.27,4.28,5.78,
4.6,4.7,4.8,4.99,5.86,6.88,7.87,8.5,4.28,7.34,4.67,3.75,
8.99,4.91,6.3,6.94,2.95,5.66]
data2=[5.26,5.17,2.37,4.18,8.07,5.52,7.34,9.96,8.72,7.31,7.9,
3.45,8.6,5.67,8.09,4.79,5.51,7.81,5.21,6.88,4.18,6.32,
7.86,6.71,5.04,6.95,6.59,6.68,6.67,5.97,6.74,7.63,4.61,
7.37,5.24,6.1,5.48,6.4,7.23,7.02,7.46,7.41,7.03,5.49,
7.43,6.06,4.15,6.45,8.23,5.98]
#sides -- 1: una cola; 2: dos colas
sides=1
def prueba_f(data1,data2,alfa,sides):
n1 = len(data1)
n2 = len(data2)
data1_mean = np.mean(data1)
data2_mean = np.mean(data2)
data1_sd = stdev( data1, data1_mean )
data2_sd = stdev( data2, data2_mean )
f_obs = data1_sd**2/data2_sd**2
p_value = f.sf(f_obs,n1-1,n2-1)*sides
if p_value > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
return f_obs,p_value,conclusion
f_obs,p_value,conclusion = prueba_f(data1,data2,alfa,sides)
print("Prueba de hipotesis de ",sides," cola.")
print("Nivel de significancia =",alfa)
print("F observado =",f_obs)
print("p valor = ",p_value)
print(conclusion)
Prueba de hipotesis de 1 cola.
Nivel de significancia = 0.05
F observado = 1.1180684754060781
p valor = 0.34778951522440243
No se rechaza la hipotesis nulaEn este caso, las observaciones correspondientes a “data1” son las del turno tarde, mientras que la “data2” son las observaciones de la mañana. Nótese también que fue necesario cargar las calificaciones de ambos turnos que, por razones de espacio, no fueron incluidas en el enunciado del problema.
Análisis de Varianza (ANOVA)
Es una prueba de hipótesis que está diseñada específicamente para probar si dos o más poblaciones tienen las mismas medias. Aún cuando el propósito de este test es hacer la prueba para hallar diferencias en las medias poblacionales, implica un examen de las varianzas muestrales, es por ello que se lo conoce como análisis de varianza o ANOVA (por sus siglas en inglés).
Utilizaremos los siguientes conceptos:
Unidades experimentales: son los objetos que reciben el tratamiento.
Factor: es la variable cuyo impacto en las unidades experimentales se desea medir.
Tratamientos: son las acciones que se aplican sobre las unidades experimentales y cuyo efecto es objeto de comparación.
Variable respuesta: es la variable observada con la que se mide el efecto del tratamiento.
Para la aplicación de la prueba ANOVA son esenciales tres supuestos:
Las muestras tienen que ser independientes.
Cada muestra debe provenir de una población normalmente distribuida.
Las varianzas de la variable de respuesta de los grupos en la población deben ser iguales entre sí. Esta propiedad se conoce como homocedasticidad.
Designando como \(c\) al número de tratamientos, tenemos que la formulación de la hipótesi es la siguiente:
\[\begin{aligned} && H_{0}\!:\; & \quad \mu_{1}=\mu_{2}=\cdots=\mu_{n} \nonumber \\ && H_{1}\!:\; & \quad \text{No todas las medias son iguales} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Esta prueba no es equivalente a probar la igualdad de varias medias utilizando varias pruebas \(t\) (ver página ) con pares de muestras. Las razones básicamente son dos:
Si el número de poblaciones se incrementa, el número de pruebas requeridas crece significativamente. Por ejemplo, si tenemos 4 tratamientos, el número de pruebas que se deben hacer son 6 (\(C_{2}^{4}\))
La segunda surge del error de tipo I. Supongamos que las pruebas se desean analizar a un nivel de significancia (\(\alpha\)) del 5%, y hay cuatro poblaciones, entonces la probabilidad del error de tipo I es: \[\begin{aligned} P(\text{Tipo I})\!=\; & (1-(1-\alpha)^{c}) \nonumber \\ \!=\; & (1-(1-0.05)\cdot(1-0.05)\cdot(1-0.05)\cdot(1-0.05)) \nonumber \\ \!=\; & 1-0.95^{4} \nonumber \\ \!=\; & 0.185 \end{aligned}\]
Mientras que se quería probar a un nivel del 5%, la necesidad de hacer cuatro pruebas incrementó la probabilidad del error tipo I más allá de los límites deseados (\(18,5\%\)).
Para determinar si tratamientos diferentes tienen efectos diferentes en sus respectivas poblaciones, se hace una comparación entre la variación de la variable respuesta dentro de las muestras (varianza dentro del grupo o within) y la variación de la variable respuesta entre muestras (varianza entre grupos o between). Entonces, podemos destacar los siguientes aspectos:
Efecto tratamiento: como las muestras diferentes tienen tratamientos distintos, la variación de la variable respuesta entre las muestras puede ser producida por los efectos de los tratamientos diferentes.
El cociente de la variación entre muestras y la variación dentro de las muestras de la variable respuesta, tal como se utiliza en ANOVA, tiene una distribución \(F\).
Cuando las medias poblacionales son diferentes, el efecto tratamiento está presente y las variaciones entre las medias de las muestras serán significativamente diferentes en comparación con las variaciones dentro de las muestras. Como consecuencia, el valor del estadístico \(F\) observado aumentará.
Para mostrar en forma general la descomposición de la varianza total, consideremos \(X_{1},X_{2},\cdots X_{n}\) variables aleatorias que se distribuyen normales, y suponiendo que además provienen de distintas poblaciones con medias \(\mu_{1},\mu_{2},\cdots \mu_{n}\) y varianzas \(\sigma ^{2}_{1},\sigma ^{2}_{2},\cdots,\sigma ^{2}_{n}\), respectivamente. Entonces, podemos calcular la variación total como: \[\begin{aligned} \text{Variación total}=\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{\overline{X}})^{2} \end{aligned}\] donde \(r_{j}\) es la cantidad de observaciones de cada tratamiento, \(c\) la cantidad de grupos (igual a la cantidad de tratamientos), y \(\overline{\overline{X}}\) la media general. Entonces, descomponiendo la variación total, tenemos: \[\begin{aligned} \sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{\overline{X}})^{2}\!=\; & \sum_{j=1}^{c}\sum_{i=1}^{r_{j}}\bigg((X_{ij}-\overline{X}_{j})+(\overline{X}_{j}-\overline{\overline{X}})\bigg)^{2} \nonumber \\ \!=\; & \sum_{j=1}^{c}\sum_{i=1}^{r_{j}}\bigg((X_{ij}-\overline{X}_{j})^{2}+2(X_{ij}-\overline{X}_{j})(\overline{X}_{j}-\overline{\overline{X}})+(\overline{X}_{j}-\overline{\overline{X}})^{2}\bigg) \nonumber \\ \!=\; & \sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{X}_{j})^{2}+2\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{X}_{j})(\overline{X}_{j}-\overline{\overline{X}})+\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(\overline{X}_{j}-\overline{\overline{X}})^{2} \nonumber \\ \!=\; & \sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{X}_{j})^{2}+2\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{X}_{j})(\overline{X}_{j}-\overline{\overline{X}})+\sum_{j=1}^{c}r_{j}(\overline{X}_{j}-\overline{\overline{X}})^{2} \nonumber \end{aligned}\] \[{\begin{aligned} \underbrace{\sum_{i=1}^{c}\sum_{j=1}^{r_j}(X_{ij}-\overline{\overline{X}})^{2}}&=\underbrace{\sum_{j=1}^{c}r_{j}(\overline{X}_{j}-\overline{\overline{X}})^{2}}+\underbrace{\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(X_{ij}-\overline{X}_{j})^{2}} \\ \textbf{SCT} \quad \qquad &\qquad \qquad \textbf{SCE} \qquad \qquad \quad \textbf{SCD} \end{aligned}}\] siendo \(X_{ij}\) la observación \(i\)-ésima en la muestra \(j\)-ésima y \(\overline{X}_{j}\) la media de cada tratamiento o grupo.
En consecuencia, podemos escribir la variación total como:
\[\begin{aligned} \textbf{Variación total}=\textbf{Variación entre grupos}+\textbf{Variación dentro del grupo} \end{aligned}\] que expresamos por: \[\begin{aligned} \text{SCT}=\text{SCE}+\text{SCD} \end{aligned}\]
Si dividimos los desvíos cuadrados medios entre grupos por los desvíos dentro de los grupos, tenemos el estadístico con distribución \(F\) a utilizar con ANOVA, es decir:
\[\begin{aligned} \frac{SCE/(c-1)}{SCD/(n-c)} & \sim & F_{(c-1),(n-c)} \nonumber \end{aligned}\] \[{ \frac{CME}{CMD} \sim F_{(c-1),(n-c)}}\] donde \(n\) es la cantidad total de observaciones. La cantidad de grados de libertad para el numerador es \((c-1)\) y para el denominador \((n-c)\).
Problema Resuelto 3.10. Deseamos medir el efecto de un programa de capacitación sobre la producción de los empleados, donde se consideran tres tipos de formación adicional posible: i) híbrido, ii) on-line y iii) curso presencial.
Consideremos los siguientes puntajes, que expresan los niveles de producción, obtenidos por 15 empleados que fueron capacitados con los distintos tratamientos:
| Tipo de Capacitación | |||
|---|---|---|---|
| Híbrido | On-line | Curso Presencial | |
| 85 | 88 | 82 | |
| 72 | 84 | 80 | |
| 83 | 91 | 85 | |
| 80 | 88 | 90 | |
| 70 | 92 | 88 | |
| \(\overline{x}_{j}\) | 78 | 88,6 | 85 |
| \(\overline{\overline{x}}\) | 83,87 | ||
| \(n\) | 15 | ||
| \(c\) | 3 | ||
Solución
Realizaremos la siguiente prueba:
Planteo de la hipótesis: \[\begin{aligned} && H_{0}\!:\; & \quad \mu_{1}=\mu_{2}=\mu_{3} \nonumber \\ && H_{1}\!:\; & \quad \text{No todas las medias son iguales} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Para calcular el estadístico \(F\) debemos obtener las sumas de los cuadrados. Primero calculamos SCE:
\[\begin{aligned} SCE=\sum_{j=1}^{c}r_{j}(\overline{x}_{j}-\overline{\overline{x}})^{2} \end{aligned}\]
| Cuadrados entre grupos | |||
|---|---|---|---|
| Híbrido | On-line | Curso Presencial | |
| 172,09 | 112,02 | 6,42 | |
| SCE | 290,53 | ||
Luego, calculamos SCD \[\begin{aligned} SCD=\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(x_{ij}-\overline{x}_{j})^{2} \end{aligned}\]
| Cuadrados dentro de los grupos | |||
|---|---|---|---|
| Híbrido | On-line | Curso Presencial | |
| 1,28 | 17,08 | 3,48 | |
| 140,82 | 0,02 | 14,95 | |
| 0,75 | 50,88 | 1,28 | |
| 14,95 | 17,08 | 37,63 | |
| 192,28 | 66,15 | 17,08 | |
| SCD | 285,20 | ||
Calculando el valor de los cuadrados medios: \[\begin{aligned} CME\!=\; & \frac{SCE}{c-1}=\frac{290,53}{3-1}=145,26 \nonumber \\ CMD\!=\; & \frac{SCD}{n-c}=\frac{285,20}{15-3}=23,76 \end{aligned}\]
Por lo que el estadístico \(F\) toma el valor: \[\begin{aligned} F^{obs}=\frac{CME}{CMD}=\frac{145,26}{23,76}=6,11 \end{aligned}\]
Recordemos que, a medida que los tratamientos tienden a producir efectos diferentes, \(CME\) lo refleja incrementándose, por lo que el valor de \(F\) aumenta.
Los grados de libertad del numerador son \((c-1)=(3-1)=2\), mientras que los grados de libertad del denominador son \((n-c)=(15-3)=12\), por lo que el valor crítico de \(F\) con un \(\alpha=0,05\) es \(F_{2;12;0.05}=3,88\). Por lo tanto, la regla de decisión será: rechazar la hipótesis nula si el valor observado supera el valor crítico de \(3,88\).
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace F_{c-1,n-c} \in \mathbb{R} > 0 \quad \vert \quad F_{c-1,n-c}>F_{c-1,n-c}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace F_{2,12} \in \mathbb{R} > 0 \quad \vert \quad F_{2,12}>3.88\rbrace \Rightarrow F^{obs}=6.11 \in \textbf{ZR} \end{aligned}\]
Gráficamente:
Conclusión: el valor \(F^{obs}=6.11\) calculado para el estadístico de la prueba nos conduce a rechazar la hipótesis nula de que las medias de las tres poblaciones sean iguales. Es decir, que hay evidencia suficiente para afirmar que los puntajes de pruebas promedio no son los mismos para los tres programas de capacitación. Existe efecto significativo del tratamiento relacionado con alguno de los programas y hay por lo menos dos medias que son distintas entre sí.
Los resultados del análisis de varianza se presentan generalmente en una tabla resumen cuyo formato es el siguiente:
| Variación | Suma de Cuadrados | Grados de Libertad | Cuadrados Medios | F | p-valor |
| Entre Grupos | \(SCE=\sum_{j}^{c}r_{j}(\overline{x}_{j}-\overline{\overline{x}})^{2}\) | \(c-1\) | \(CME=\frac{SCE}{c-1}\) | \(F=\frac{CME}{CMD}\) | \(p\) |
| Dentro de los Grupos | \(SCD=\sum_{j}^{c}\sum_{i}^{r_{j}}(x_{ij}-\overline{x}_{j})^{2}\) | \(n-c\) | \(CMD=\frac{SCD}{n-c}\) | ||
| Total | \(SCT=\sum_{j}^{c}\sum_{i}^{r_{j}}(x_{ij}-\overline{\overline{x}})^{2}\) | \(n-1\) | \(CMT=\frac{SCT}{n-1}\) | ||
En este caso particular, la Tabla de ANOVA es:
| Variación | Suma de Cuadrados | Grados de Libertad | Cuadrados Medios | F | p-valor |
| Entre Grupos | \(SCE=290.53\) | \(3-1\) | \(CME=\frac{290.53}{3-1}\) | \(F=6.11\) | \(0.015\) |
| Dentro de los Grupos | \(SCD=285.20\) | \(15-3\) | \(CMD=\frac{285.20}{15-3}\) | ||
| Total | \(SCT=575.73\) | \(15-1\) | \(CMT=\frac{575.73}{15-1}\) | ||
Cuando el cociente calculado para \(F\) en la tabla ANOVA es mayor que el correspondiente valor crítico de tabla, la hipótesis nula es rechazada, aceptándose, en consecuencia, la hipótesis alternativa de que todas las medias no son iguales, es decir que una o más son diferentes. En este caso, surge la pregunta ¿Cúal o cuáles de las medias son diferentes? Para responder a este interrogante deberemos utilizar métodos de comparaciones múltiples, como la Prueba de Tukey-Kramer que se verá en el siguiente capítulo (página ).
Para tener en cuenta:
Existen tests para verificar si se cumplen las condiciones del ANOVA. Por ejemplo, para homogeneidad de varianzas están las pruebas de Bartlett, Q de Cochran y Hartley (ver página ); para contrastar la normalidad, el test de Shapiro-Wilk
Alternativamente al ANOVA, existen otros test no paramétricos de análisis de varianza. Por ejemplo, Test de Kruskal Wallis
Pruebas de Hipótesis No Paramétricas
A diferencia de las pruebas parámetricas, en las cuales se hacen supuestos acerca de distribución de la población, las pruebas no paramétricas son aquellas que tienen como denominador común que no requieren que la distribución de la población sea caracterizada por ciertos parámetros. En este capítulo veremos las principales pruebas que se suelen usar en la práctica, aunque existe un gran número de pruebas no paramétricas.
Prueba para Comparación de Varianzas de dos o más Poblaciones
Para comparar varianzas de dos o más poblaciones también se puede usar la prueba no paramétrica de Hartley, cuya ventaja principal es que pueden compararse varianzas de más de dos poblaciones.
Prueba de Hartley
Esta es una prueba para comparar varianzas de dos o más poblaciones. La hipótesis de la prueba es:
\[ \begin{aligned} H_{0}\!:\; & \sigma_{1}^{2}=\sigma_{2}^{2}=\cdots=\sigma_{n}^{2} \\ H_{1}\!:\; & \text{Alguna varianza es distinta}\ \textbf{Prueba lateral derecha} \end{aligned} \]
El estadístico de esta prueba es el llamado \(F_{max}\) que sigue la distribución de Hartley y que se define como: \[{ \frac{S^{2}_{max}}{S^{2}_{min}} \sim F_{max \quad c,(\overline{n}-1)}}\] donde \(S^{2}_{max}\) es la mayor y \(S^{2}_{min}\) la menor varianza muestral, \(c\) es la cantidad de poblaciones, \(\overline{n}=\textit{Int} \lfloor \frac{n}{c} \rfloor\), es decir la parte entera de \(n/c\), en el que \(n\) es el número de observaciones. Los valores de \(F_{max}\) están tabulados y, al ser una prueba lateral derecha, se rechaza \(H_{0}\) cuando el \(F_{max}^{obs}>F_{max}^{crit}\).
Prueba de Independencia
En esta prueba se busca analizar la existencia o no de independencia estadística entre dos variables cualitativas de una población. Para ello se toma una muestra y se analiza una tabla de doble entrada con las dos variables cualitativas de interés. Luego se comparan las frecuencias absolutas observadas y esperadas, y a través del estadístico \(\chi^{2}\) se concluye que las variables son independientes cuando las diferencias son no siginificativas, o dependientes en caso contrario.
Las hipótesis que se deben plantear en esta prueba siempre son las mismas y no pueden ser modificadas, donde: \[\begin{aligned} && H_{0}\!:\; & \quad \text{Las variables son independientes} \nonumber \\ && H_{1}\!:\; & \quad \text{Las variables NO son independientes} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Supongamos que tomamos una muestra de tamaño \(n\), y se recoleta la información para dos variables cualitativas donde cada una tiene dos posibles respuestas (A o B, y I y II respectivamente). Entonces, si construimos una tabla de doble entrada, tenemos:
| Variable 2 | |||
|---|---|---|---|
| Variable 1 | I | II | Total |
| A | \(f^{o}_{11}\) | \(f^{o}_{12}\) | \(f^{o}_{1.}\) |
| B | \(f^{o}_{21}\) | \(f^{o}_{22}\) | \(f^{o}_{2.}\) |
| Total | \(f^{o}_{.1}\) | \(f^{o}_{.2}\) | \(n\) |
donde \(f^{o}_{ij}\) es la frecuencia absoluta observada9 de la fila \(i\) y columna \(j\) para todo \(i=1,2\) y \(j=1,2\); \(f^{o}_{i.}\) es la frecuencia absoluta observada en la fila \(i\) y, \(f^{o}_{.j}\) la frecuencia absoluta observada de la columna \(j\). Suponiendo que queremos estudiar la independencia de las variables 1 y 2, el estadístico \(\chi^{2}\) de la prueba será:
\[{ \sum_{i=1}^{n_{f}}\sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}} \sim \chi^{2}_{(n_{f}-1)(n_{c}-1)}}\] donde \(n_{f}\) es cantidad de filas y \(n_{c}\) la cantidad de columnas.
La cantidad de grados de libertad asociados al estadístico viene dada por \((n_{f}-1)(n_{c}-1)\), y las frecuencias esperadas se calculan como:
\[\label{estimador_chi2_indep} { f^{e}_{ij}=\frac{f^{o}_{i.}\cdot f^{o}_{.j}}{n}}\]
En el caso particular de la tabla anterior, la cantidad de filas es \(n_{f}=2\) y la cantidad de columnas es \(n_{c}=2\). Este estadístico no proviene de ningún parámetro, por lo que los supuestos con los que se aplica son mucho menos restrictivos que las pruebas paramétricas. La única condición que se debe cumplir es que las frecuencias esperadas de cada una de las celdas debe ser mayor a 5, es decir:
\[\begin{aligned} f^{e}_{ij}>5 \quad \forall \quad i,j \end{aligned}\]
En el caso de no cumplirse esta condición, y si se supone que el valor esperado de la celda de la fila k-ésima y columna n-ésima tiende a cero (\(f^{e}_{kn}\to 0\)) y su correspondiente valor observado es mayor que cero (\(f^{o}_{kn}>0\)), tendríamos:
\[\begin{aligned} \lim_{f^{e}_{ij} \to 0} \chi^{2}_{(n_{f}-1)(n_{c}-1)}\!=\; & \lim_{f^{e}_{ij} \to 0} \sum_{i=1}^{n_{f}} \sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}} \nonumber \\ \!=\; & \sum_{i=1}^{n_{f}} \sum_{j=1}^{n_{c}} \lim_{f^{e}_{ij} \to 0} \frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}} \nonumber \\ \!=\; & \lim_{f^{e}_{kn} \to 0} \frac{(f^{o}_{kn}-f^{e}_{kn})^{2}} {f^{e}_{kn}} + K \nonumber \\ \!=\; & \infty \end{aligned}\] donde \(K\) representa al valor de todos los otros términos distintos a la celda de la fila k-ésima y columna n-ésima.
Como podemos apreciar, al ser una prueba lateral derecha, el estadístico siempre caería en zona de rechazo de \(H_{0}\) para cualquier valor de \(\alpha\), con lo que la prueba no podría ser aplicada. La solución de este problema es realizar una agrupación de filas o de columnas hasta que las frecuencias esperadas sean mayores que 510 para cada una de las celdas.
Otra manera de analizar esta condición es considerando que cada celda es un variable binomial \(X\), es decir dicotómica. Como estamos trabajando con un estadístico \(\chi^{2}\) que es la suma de variables aleatorias normales estándares independiente elevadas al cuadrado, para que una binomial se aproxime a la normal estándar se debe cumplir la condición del Teorema de De Moivre - Laplace, es decir que \(X \sim N(n\cdot p,\sqrt{n\cdot p \cdot (1-p)})\) si \(n\geq 30\), \(np\geq 5\) y \(n(1-p)\geq 5\) (ver página ).
Problema Resuelto 4.1. El Gobierno sabe que durante los últimos años aumentó el número de matrículas en escuelas privadas en relación a las escuelas públicas. Además, cree que las familias de altos ingresos tienden a enviar a sus hijos a escuelas privadas y que las familias de bajos ingresos los envían a escuelas públicas. Para confirmar o desechar esta presunción, decide tomar una muestra aleatoria de 1600 familias obteniendo los siguientes resultados:
| Escuela | |||
|---|---|---|---|
| Ingresos | Privada | Publica | Total |
| Bajos | 506 | 494 | 1 000 |
| Altos | 438 | 162 | 600 |
| Total | 944 | 656 | 1 600 |
¿A qué conclusión llega a un nivel de significancia del 5%?
Solución
Dado que se pretende analizar la independencia (o no) de las variables de ingresos familiares y el tipo de escuela (público o privada) a la que asisten los hijos, se plantea lo siguiente:
Planteo de la hipótesis: \[\begin{aligned} && H_{0}\!:\; & \quad \text{Las variables ingresos y tipo de escuela son independientes} \nonumber \\ && H_{1}\!:\; & \quad \text{Las variables ingresos y tipo de escuela NO son independientes} \nonumber \end{aligned}\]
Lo primero que debemos hacer es calcular las frecuencias esperadas. Para ello, usaremos el estimador de la ecuación ([estimador_chi2_indep]), es decir que, para la primer celda (ingresos Bajos y escuela Privada), tenemos:
\[\begin{aligned} f^{e}_{11}\!=\; & \frac{f^{o}_{1.}\cdot f^{o}_{\text{.}1}}{n} \nonumber \\ \!=\; & \frac{944 \cdot 1\,000}{1\,600}=590 \end{aligned}\]
Procediendo de igual manera para las otras celdas, se llega a que las frecuencias esperadas son:
| Frecuencias Esperadas | |||
|---|---|---|---|
| Ingresos | Privada | Publica | Total |
| Bajos | 590 | 410 | 1 000 |
| Altos | 354 | 246 | 600 |
| Total | 944 | 656 | 1 600 |
Se puede observar que todas las frecuencias esperadas son mayores que 5, con lo cual se cumple el requisito para que la aproximación del teorema de De Moivre - Laplace sea válida. Por otra parte, cabe destacar que las frecuencias esperadas pueden tomar valores fraccionarios, mientras que las frecuencias observadas son siempre enteras. Posteriormente, calculando las diferencias al cuadrado entre frecuencias observadas y esperadas y dividiendo por la frecuencia esperada para cada celda, obtenemos los términos de la suma que arroja el valor del estadístico:
| Términos del estadístico \(\chi^{2}\) | ||
|---|---|---|
| Ingresos | Privada | Publica |
| Bajos | 12.0 | 17.2 |
| Altos | 19.9 | 28.7 |
\[\begin{aligned} \chi^{2}_{obs}=\sum_{i=1}^{n_{f}}\sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}}=12.0+17.2+19.9+28.7=77.78 \end{aligned}\]
La zona de rechazo, teniendo en cuenta los grados de libertad \((f-1)(c-1)=(2-1)(2-1)=1\) y que estamos trabajando con un \(\alpha=0.05\), es entonces: \[\begin{aligned} \textbf{ZR}\!=\; & \lbrace \chi^{2}_{(n_{f}-1)(n_{c}-1)} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{(n_{f}-1)(n_{c}-1)}>\chi^{2}_{crit} \rbrace \nonumber \\ \!=\; & \lbrace \chi^{2}_{1} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{1}>6.64 \rbrace \Rightarrow \chi^{2}_{obs}=77.78 \in \textbf{ZR} \end{aligned}\]
Como conclusión, se rechaza \(H_{0}\), por lo que las variables ingreso y tipo de escuela son dependientes a un nivel de significancia del 5%.
El código para solucionar el problema en Python es el siguiente:
#Librerias
from scipy.stats import chi2_contingency
# Nivel de significancia
alfa=0.05
# Datos muestrales en formato de tabla
table = [[506,494],[438,162]]
chi2_obs, p_value, dof, expected = chi2_contingency(table, correction=False)
print("Frecuencias Observadas:", table)
print("Frecuencias Esperadas:", expected)
print("Grados de Libertad =", dof)
print("Chi2 observado =",chi2_obs)
print("p valor = ",p_value)
if p_value < alfa:
print("Se rechaza la hipotesis nula")
else:
print("No se rechaza la hipotesis nula")
Frecuencias Observadas: [[506, 494], [438, 162]]
Frecuencias Esperadas: [[590. 410.]
[354. 246.]]
Grados de Libertad = 1
Chi2 observado = 77.78420835055809
p valor = 1.1493539476186201e-18
Se rechaza la hipotesis nulaA tener en cuenta: los datos deben ser ingresados en forma de tabla, donde cada fila se presenta entre corchetes y la coma separa las filas. El comando “correction=False” es para que utilice el estimador ([estimador_chi2_indep]), con la opción “True” realiza la corrección de Yates11 al estimador.
Prueba de Homogeneidad
La prueba \(\chi^{2}\) desarrollada en el punto anterior (sección 4.2), también se puede aplicar para determinar si dos o más muestras aleatorias independientes se extraen de una misma población. Para ello se clasifica a la población en términos de una variable cualitativa en \(k\) grupos (categorías de la variable), con el objetivo de evaluar si las proporciones poblacionales son homogéneas. Es decir, se plantea la hipótesis siguiente:
\[\begin{aligned} && H_{0}\!:\; & \quad \pi_{1}=\pi_{2}=\cdots =\pi_{k} \nonumber \\ && H_{1}\!:\; & \quad \text{Alguna de las proporciones es distinta} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
El estadístico de la prueba de homogeneidad será idéntico al estadístico de la prueba de independencia:
\[{\sum_{i=1}^{n_{f}}\sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}} \sim \chi^{2}_{(n_{f}-1)(n_{c}-1)}}\]
Problema Resuelto 4.2. Se pretende analizar la intención de voto para las próximas elecciones a gobernador de una provincia. A tal fin se realiza una encuesta a 115 profesionales, 110 empresarios y 125 empleados en relación de dependencia, a quienes se les pregunta sobre su intención de voto respecto del candidato A o del candidato B, ambos postulados para ser gobernador de la provincia. Los resultados obtenidos son:
| Frecuencias Observadas | |||
|---|---|---|---|
| Candidato | |||
| Grupo de personas | A | B | Total |
| Profesionales (P) | 80 | 35 | 115 |
| Empresarios (E) | 72 | 38 | 110 |
| Empleados (ERD) | 69 | 56 | 125 |
| Total | 221 | 129 | 350 |
¿Existe diferencia de opinión entre los tres grupos de personas a un nivel de significancia del 10%?
Solución
Cuando se quieren comparar proporciones de distintas poblaciones, estamos ante la presencia de una prueba de homogeneidad. La hipótesis de esta prueba viene dada por:
\[\begin{aligned} && H_{0}\!:\; & \quad \pi^{A}_{P}=\pi^{A}_{E} =\pi^{A}_{ERD} \nonumber \\ && H_{1}\!:\; & \quad \text{Alguna de las proporciones es distinta} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Y el estadístico es:
\[\begin{aligned} \sum_{i=1}^{n_{f}}\sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}} \sim \chi^{2}_{(n_{f}-1)(n_{c}-1)} \end{aligned}\]
Calculando las frecuencias esperadas haciendo uso del estimador ([estimador_chi2_indep]), se tiene:
\[\begin{aligned} f^{e}_{ij}\!=\; & \frac{f^{o}_{i.}\cdot f^{o}_{.j}}{n} \end{aligned}\]
| Frecuencias Esperadas | |||
|---|---|---|---|
| Candidato | |||
| A | B | Total | |
| Profesionales | 72.61 | 42.39 | 115 |
| Empresarios | 69.46 | 40.54 | 110 |
| Empleados | 78.93 | 46.07 | 125 |
| Total | 221 | 129 | 350 |
Con la tabla anterior, se puede ver que las frecuencias esperadas de todas las celdas son mayores que 5, con lo cual se satisfacen las condiciones impuestas para la prueba de hipótesis. Luego, calculando las diferencias al cuadrado entre frecuencias observadas y esperadas y dividiendo por la frecuencia esperada para cada celda, llegamos a:
| Términos del estadístico \(\chi^{2}\) | ||
|---|---|---|
| A | B | |
| Profesionales | 0.8 | 1.3 |
| Empresarios | 0.1 | 0.2 |
| Empleados | 1.2 | 2.1 |
Entonces:
\[\begin{aligned} \chi^{2}_{obs}\!=\; & \sum_{i=1}^{n_{f}}\sum_{j=1}^{n_{c}}\frac{(f^{o}_{ij}-f^{e}_{ij})^{2}}{f^{e}_{ij}}\nonumber \\ \!=\; & 0.8+1.3+0.1+0.2+1.2+2.1=5.7 \end{aligned}\]
La zona de rechazo, teniendo en cuenta los grados de libertad \((n_{f}-1)(n_{c}-1)=(3-1)(2-1)=2\) y que estamos trabajando con \(\alpha=0.10\), entonces:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace \chi^{2}_{(n_{f}-1)(n_{c}-1)} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{(n_{f}-1)(n_{c}-1)}>\chi^{2}_{crit} \rbrace \nonumber \\ \!=\; & \lbrace \chi^{2}_{2} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{2}>4..60 \rbrace \Rightarrow \chi^{2}_{obs}=5.70 \in \textbf{ZR} \end{aligned}\]
Entonces, se rechaza \(H_{0}\), por lo que las proporciones de intención de voto de los distintos grupos de votantes no es la misma, a un nivel de significancia del 10%. En otros términos, las tres poblaciones (Profesionales, Empresarios y Empleados) no son homogéneas (no son iguales) en cuanto a la intención de voto.
Gráficamente tenemos:
Prueba de Marascuilo
Cuando la hipótesis nula es rechazada en la prueba de homogeneidad, aceptándose en consecuencia la hipótesis alternativa de que todas las proporciones no son iguales, es decir que una o más son diferentes, surge la pregunta ¿Cuáles son diferentes? Para responder este interrogante deberemos utilizar métodos de comparaciones múltiples. Una de esas pruebas es la de Prueba de Marascuilo.
Este procedimiento nos permite probar simultáneamente las diferencias de todos los pares posibles de proporciones cuando hay varias poblaciones bajo estudio y determinar cuál o cuáles proporciones son distintas.
Si \(\pi_{1}, \pi_{2},\cdots ,\pi_{c}\) son las verdaderas proporciones de las \(c\) poblaciones, sus estimadores son \(P_{1},P_{2},\cdots,P_{c}\), entonces se construye el parámetro poblacional \(\theta_{j}=\pi_{j}-\pi_{i}\), por lo que su estimador vendrá dado por \(\widehat{\theta}_{ji}=P_{j}-P_{i}\). Se puede demostrar que dicho estimador debe ser comparado con el siguiente punto crítico:
\[\label{maracuillo0} { m_{ji}=\sqrt{\chi^{2}_{c-1,1-\alpha}}\sqrt{\frac{P_{j}(1-P_{j})}{n_{j}}+\frac{P_{i}(1-P_{i})}{n_{i}}}}\]
Entonces la regla de decisión será la siguiente:
Si \(\vert \widehat{\theta}_{ji} \Big\vert > m_{ji}\) significa que hay diferencias significativas entre las dos proporciones poblacionales comparadas.
Problema Resuelto 4.3. Continuando con el problema 4.2, ¿Qué categorías de personas encuestadas es la que opina diferente con un nivel de significancia del 10%?
Solución
En el problema 4.2 se rechazó la hipótesis nula de que todas las proporciones son iguales, por lo que continuamos con la prueba de Marascuilo para poder diferenciar cuáles son las poblaciones con proporciones diferentes. En primer lugar calcularemos las proporciones de votos al candidato A en la muestra:
\[\begin{aligned} p^{A}_{P}\!=\; & \frac{80}{115}=0.696 \nonumber \\ p^{A}_{E}\!=\; & \frac{72}{110}=0.654 \nonumber \\ p^{A}_{ERD}\!=\; & \frac{69}{125}=0.552 \nonumber \\ \end{aligned}\]
Luego, teniendo en cuenta que \(\chi^{2}_{c-1,1-\alpha}=\chi^{2}_{2,0.90}=4.60\) podemos calcular los puntos críticos, aplicando ([maracuillo0]):
\[\begin{aligned} m_{P-E}\!=\; & \sqrt{\chi^{2}_{c-1,1-\alpha}}\sqrt{\frac{p^{A}_{P}(1-p^{A}_{P})}{n_{P}}+\frac{p^{A}_{E}(1-p^{A}_{E})}{n_{E}}} \nonumber \\ \!=\; & \sqrt{4.60}\sqrt{\frac{0.696(1-0.696)}{115}+\frac{0.654(1-0.654)}{110}}=0.134 \end{aligned}\]
Procediendo de igual forma calculamos:
\[\begin{aligned} m_{P-ERD}\!=\; & \sqrt{\chi^{2}_{c-1,1-\alpha}}\sqrt{\frac{p^{A}_{P}(1-p^{A}_{P})}{n_{P}}+\frac{p^{A}_{ERD}(1-p^{A}_{ERD})}{n_{ERD}}} \nonumber \\ \!=\; & \sqrt{4.60}\sqrt{\frac{0.696(1-0.696)}{115}+\frac{0.552(1-0.552)}{125}}=0.133 \\ m_{E-ERD}\!=\; & \sqrt{\chi^{2}_{c-1,1-\alpha}}\sqrt{\frac{p^{A}_{E}(1-p^{A}_{E})}{n_{E}}+\frac{p^{A}_{ERD}(1-p^{A}_{ERD})}{n_{ERD}}} \nonumber \\ \!=\; & \sqrt{4.60}\sqrt{\frac{0.654(1-0.654)}{110}+\frac{0.552(1-0.552)}{125}}=0.136 \end{aligned}\]
Por último, debemos comparar el estadístico \(\widehat{\theta}_{ji}=P_{j}-P_{i}\) con los puntos críticos calculados, es decir:
\[\begin{aligned} \vert \widehat{\theta}_{P-E} \Big\vert = \Big\vert p^{A}_{P}-p^{A}_{E} \Big\vert \!=\; & \vert 0.696-0.654 \Big\vert = 0.042 < m_{P-E} = 0.134 \nonumber \\ \vert \widehat{\theta}_{P-ERD} \Big\vert = \Big\vert p^{A}_{P}-p^{A}_{ERD} \Big\vert \!=\; & \vert 0.696-0.553 \Big\vert = 0.144 > m_{P-ERD} = 0.133 \nonumber \\ \vert \widehat{\theta}_{E-ERD} \Big\vert = \Big\vert p^{A}_{E}-p^{A}_{ERD} \Big\vert \!=\; & \vert 0.654-0.553 \Big\vert = 0.102 < m_{E-ERD} = 0.136 \nonumber \\ \end{aligned}\]
Como conclusión, existen diferencias significativas entre las proporciones de las categorías de Profesionales y Empleados en Relación de Dependencia a un nivel de significancia del 10%, siendo mayor la intención de votos en los Profesionales por el candidato A.
Prueba de Bondad de Ajuste \(\chi^{2}\)
Esta es una prueba para decidir, a partir de una muestra particular, si se rechaza o no la hipótesis de que una variable aleatoria se ajusta a una distribución probabilística específica.
El procedimiento comienza con el planteo de la hipótesis nula de que la variable aleatoria bajo estudio tiene una distribución específica. Es decir, suponiendo que estamos estudiando la variable aleatoria \(X\), entonces:
\[\begin{aligned} && H_{0}\!:\; & \quad X \sim f(\theta) \nonumber \\ && H_{1}\!:\; & \quad X \nsim f(\theta) \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
El estadístico de esta prueba viene dado por:
\[{ \chi^{2}=\sum{\frac{\left( f^{o}_{i}-f^{e}_{i} \right)^{2}} {f^{e}_{i}}} \quad \text{con $k-p-1$ grados de libertad}}\] donde \(k\) es el número de categorías de la variable y \(p\) el número de parámetros desconocidos de dicha variable que se deben estimar.
Problema Resuelto 4.4. Se tienen los datos históricos que corresponden al número de llamadas de una central de emergencias de la ciudad de Buenos Aires. El objetivo es encontrar un modelo que explique el comportamiento de las llamadas a fin de establecer la cantidad de unidades móviles, policías, médicos y bomberos necesarias para atender la demanda. Se obtiene una muestra aleatoria de 100 intervalos de 15 minutos y se registran las frecuencias de llamadas solicitando el servicio, tal como se muestra en la siguiente tabla:
| Numero de llamadas | Cantidad de intervalos |
|---|---|
| 0 | 20 |
| 1 | 52 |
| 2 | 15 |
| 3 | 10 |
| 4 | 3 |
| Total | 100 |
Con un nivel de significancia del 5%, probar si la distribución de Poisson es apropiada para describir el número de llamadas a la central.
Solución
En esta ocasión estamos interesados en conocer si la variable número de llamadas que ingresan al centro de emergencia se distribuye como Poisson. Recordemos que la distribución de Poisson viene dada por:
\[\begin{aligned} \label{poisson} f(k,\lambda)=\frac{e^{-\lambda}\lambda^{k}}{k !} \end{aligned}\]
La prueba de hipótesis que se plantea para este problema es:
Planteo de hipótesis: \[\begin{aligned} && H_{0}\!:\; & \quad \text{El número de llamadas sigue una distribución de Poisson} \nonumber \\ && H_{1}\!:\; & \quad \text{El número de llamadas NO sigue una distribución de Poisson} \nonumber \end{aligned}\]
Dado que no se conoce el parámetro \(\lambda\), tendremos que estimarlo, por lo que perderemos un grado de libertad. La estimación de \(\lambda\) viene dada por:
\[\begin{aligned} \label{lambda} \lambda=\frac{\sum x_{i}}{n}\!=\; & \frac{0 \cdot 20 +1\cdot 52 + \cdots + 4 \cdot 3}{100}=1.24 \quad \text{llamadas por intervalo} \end{aligned}\]
Usando la función de Poisson ([poisson]) y el valor estimado \(\lambda=1.24\), calculamos la probabilidad de cada número de llamadas de la tabla, teniendo en cuenta que la última categoría corresponde a 4 llamadas o más. Luego, multiplicamos dichas probabilidades por el tamaño de la muestra (\(n=100\)) para así obtener las cantidades esperadas de cada categoría. Es decir:
| Numero de llamadas | Cantidad de intervalos observados (\(f^{o}\)) | Probabilidad | Cantidad de intervalos esperados (\(f^{e}\)) |
| 0 | 20 | 0.289 | 28.94 |
| 1 | 52 | 0.359 | 35.88 |
| 2 | 15 | 0.222 | 22.25 |
| 3 | 10 | 0.092 | 9.20 |
| 4 ó + | 3 | 0.037 | 3.73 |
| Total | 100 | 1.00 | 100.00 |
| \(\lambda\) | 1.24 |
En este caso, la última categoría (4 ó +) no cumple con la condición que las frecuencias esperadas sean mayor que 5, por lo que deberemos agrupar con el número de llamadas inmediato anterior y rehacer todo el cálculo, incluyendo la estimación de \(\lambda\). Repitiendo el procedimiento, ahora con cuatro categorías (\(k=4\)), llegamos a:
| Numero de llamadas | Cantidad de intervalos observados (\(f^{o}\)) | Probabilidad | Cantidad de intervalos esperados (\(f^{e}\)) | \(\frac{\left( f^{o}_{i}-f^{e}_{i} \right)^{2}} {f^{e}_{i}}\) |
| 0 | 20 | 0.298 | 29.82 | 3.23 |
| 1 | 52 | 0.361 | 36.08 | 7.02 |
| 2 | 15 | 0.218 | 21.83 | 2.14 |
| 3 ó + | 13 | 0.123 | 12.27 | 0.04 |
| Total | 100 | 1.00 | 100.00 | |
| \(\lambda\) | 1.21 |
\[\begin{aligned} \chi^{2}_{obs}=\sum{\frac{\left( f^{o}_{i}-f^{e}_{i} \right)^{2}} {f^{e}_{i}}}=12.44 \end{aligned}\]
El punto crítico con \(k-p-1=4-1-1=2\) grados de libertad y \(\alpha\) del 5% es de \(5.99\), por lo que la zona de rechazo se define de la siguiente manera:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace \chi^{2}_{k-p-1} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{k-p-1}>\chi^{2}_{crit} \rbrace \nonumber \\ \!=\; & \lbrace \chi^{2}_{2} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{2}>5.99 \rbrace \Rightarrow \chi^{2}_{obs}=12.44 \in \textbf{ZR} \end{aligned}\]
En conclusión, se rechaza la hipótesis nula, por lo que la variable número de llamadas al centro de emergencias no sigue una distribución de Poisson.
La representación gráfica es:
Problema Resuelto 4.5. Con el fin de ajustar el periodo de garantía que ofrece una empresa que vende computadoras, registró el número de requerimientos técnicos solicitados durante el período de garantía de 3 años. Los resultados se muestran en la siguiente tabla:
| Mes | Cantidad de requerimientos |
|---|---|
| De 0 a 6 | 60 |
| más de 6 a 12 | 150 |
| más de 12 a 18 | 250 |
| más de 18 a 24 | 130 |
| más de 24 a 30 | 70 |
| más de 30 a 36 | 40 |
| Total | 700 |
A un nivel de significancia del 5% ¿puede probar que el tiempo que transcurre hasta que se efectúa el requerimiento técnico se distribuye normal?
Solución
Dado que estamos interesados en saber si los datos registrados siguen una distribución normal, la prueba de hipótesis es:
\[\begin{aligned} && H_{0}\!:\; & \quad \text{El tiempo transcurrido se distribuye normal} \nonumber \\ && H_{1}\!:\; & \quad \text{El tiempo transcurrido NO se distribuye normal} \nonumber \end{aligned}\]
La distribución normal viene dada por dos parámetros, \(\mu\) y \(\sigma^{2}\), y ninguno está especificado, por lo que se deberán calcular con los datos muestrales.
Para ello se determina el punto medio12 de cada intervalo y se obtienen:
\[\begin{aligned} \overline{x}\!=\; & \frac{\sum_{i} x_{i}^{medio}\cdot n_{i}}{n} \nonumber \\ \!=\; & \frac{60 \cdot 3 + 150 \cdot 9 + \cdots + 40 \cdot 33}{700}=16.03 \end{aligned}\]
\[\begin{aligned} s^{2}\!=\; & \frac{\sum_{i} n_{i}(x_{i}-\overline{x})^{2}}{n-1} \nonumber \\ \!=\; & \frac{60(3-16.03)^{2}+\cdots +40(33-16.03)^{2}}{700-1}=58.68 \end{aligned}\]
Una vez que tenemos \(\overline{x}\) y \(s^{2}\), que son los estimadores de \(\mu\) y \(\sigma^{2}\), necesitamos calcular la probabilidad de ocurrencia de cada intervalo de la distribución normal con esos parámetros. Para ello estandarizamos los límites de los intervalos, teniendo en cuenta que el mínimo del primer intervalo incluye todos los valores desde \(-\infty\) y el máximo del último intervalo todos los valores hasta \(+\infty\).
Una vez que tenemos los límites estandarizados (\(Z\)) de cada intervalo, calculamos las probabilidades haciendo uso de una tabla de distribución normal estándar.
Por último, las frecuencias esperadas vendrán dadas por la multiplicación de la probabilidad de ocurrencia de ese intervalo por el tamaño de la muestra \(n\). Entonces, ahora estamos en condiciones de obtener el valor del estadístico \(\chi^{2}_{obs}\) de la prueba:
\[\begin{aligned} \chi^{2}_{obs}=\sum{\frac{\left( f^{o}_{i}-f^{e}_{i} \right)^{2}} {f^{e}_{i}}}=0.67+\cdots + 10.91=31.71 \end{aligned}\]
La siguiente tabla muestra el detalle de los cálculo de realizados.
| Mes | Cantidad requerida (\(f^{o}\)) | Punto medio | \(n_{i}(x_{i}-\overline{x})^{2}\) | Z | Prob. | Frec esp (\(f^{e}\)) | \(\frac{(f^{o}-f^{e})^{2}}{f^{e}}\) | |
| min | max | |||||||
| De 0 a 6 | 60 | 3 | 10184,6 | \(-\infty\) | -1,31 | 0,0952 | 66,67 | 0,67 |
| + de 6 a 12 | 150 | 9 | 7410,1 | -1,31 | -0,53 | 0,2042 | 142,97 | 0,35 |
| + de 12 a 18 | 250 | 15 | 264,5 | -0,53 | 0,26 | 0,3021 | 211,44 | 7,03 |
| + de 18 a 24 | 130 | 21 | 3213,0 | 0,26 | 1,04 | 0,2494 | 174,59 | 11,39 |
| + de 24 a 30 | 70 | 27 | 8426,1 | 1,04 | 1,82 | 0,1149 | 80,46 | 1,36 |
| + de 30 a 36 | 40 | 33 | 11521,2 | 1,82 | \(+\infty\) | 0,0341 | 23,86 | 10,91 |
| Total | 700 | 1,0000 | 700 | 31,71 | ||||
Los grados de libertad de esta prueba son \(k-p-1=6-2-1=3\), donde \(p=2\) dado que se estimaron los parámetros \(\mu\) y \(\sigma^{2}\). Además, se verifica que las cantidades esperadas de cada intervalo cumplen con la condición de ser mayores que 5. Luego, tenemos que la zona de rechazo es:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace \chi^{2}_{k-p-1} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{k-p-1}>\chi^{2}_{crit} \rbrace \nonumber \\ \!=\; & \lbrace \chi^{2}_{3} \in \mathbb{R} > 0 \quad \vert \quad \chi^{2}_{3}>7.82 \rbrace \Rightarrow \chi^{2}_{obs}=31.71 \in \textbf{ZR} \end{aligned}\]
En conclusión, se rechaza \(H_{0}\), por lo que el tiempo transcurrido hasta que se efectúa el requerimiento técnico no sigue una distribución normal a un nivel de significancia del 5%.
Prueba de Tukey-Kramer
Este test permite responder a la pregunta planteada en la Prueba de ANOVA (ver página ) y está basado en el recorrido, o rango studentizado, que tiene un error de tipo I constante para todas las comparaciones de medias de a pares. La prueba determina que dos medias son significativamente diferentes si el valor absoluto de sus diferencias muestrales excede a:
\[\label{TK} { T_{ij}=q_{c,(n-c),\alpha}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{i}}+\frac{1}{r_{j}}\right)}}\] donde \(q\) es una variable aleatoria que corresponde al rango studentizado, la cual se encuentra tabulada para diferentes valores de \(c\) (cantidad de tratamiento) y los grados de libertad del error \((n-c)\), donde \(n\) representa el tamaño de la muestra, \(r_{i}\) es el tamaño de la muestra del grupo \(i\) y, \(r_{j}\) es tamaño de la muestra del grupo \(j\)
Problema Resuelto 4.6. Continuando con el problema planteado en la página , ahora se desea medir cuál o cuáles de los programa de capacitación sobre la producción de los empleados son diferentes entre sí, a un nivel de significancia del 5%.
Solución
Aplicando el test de Tukey-Kramer para todas las combinaciones de los grupos, teniendo en cuenta que, en este caso, el valor que figura en la tabla \(q_{3;12;0,05}=3.77\) y que, todas los grupos poseen el mismo tamaño de muestra (\(r_{i}=r_{j}=r\)), por lo cual el valor del punto crítico \(T_{ij}\) será el mismo para todas las combinaciones de grupos, tenemos:
\[\begin{aligned} T_{ij}\!=\; & q_{c,(n-c),\alpha}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{j}}+\frac{1}{r_{i}}\right)} \nonumber \\ \!=\; & q_{3;12;0,05}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r}+\frac{1}{r}\right)} \nonumber \\ \!=\; & q_{3;12;0,05}\times \sqrt{\frac{CMD}{r}} \nonumber \\ \!=\; & 3.77 \times \sqrt{\frac{23,76}{5}}=8.22 \nonumber \end{aligned}\]
Comparando el valor absoluto de cada par de diferencias de medias muestrales con el punto crítico del estimador de la prueba, tenemos:
| Grupos | Medias | Dif de Medias | \(T_{ij}\) | Conclusión | ||
|---|---|---|---|---|---|---|
| Híbrido | On-line | 78,00 | 88,60 | 10,60 | 8,22 | Hay diferencias |
| Híbrido | Curso Presencial | 78,00 | 85,00 | 7,00 | 8,22 | No hay diferencias |
| On-line | Curso Presencial | 88,60 | 85,00 | 3,60 | 8,22 | No hay diferencias |
En consecuencia, podemos concluir que existe efecto significativo y positivo (mayor productividad) del tratamiento relacionado con el programa de capacitación “On-line” en comparación con el “Híbrido” a un nivel de significancia del 5%.
Problema Resuelto 4.7. En la cátedra de una materia de una carrera universitaria se asignaron en forma aleatoria 26 alumnos a tres modalidades de examen final: oral, escrito con desarrollo y en computadora. El objetivo es definir la mejor forma de evaluación, en función de la nota final obtenida por los alumnos, a fin de implementarla en los años siguientes. Las notas obtenidas por este grupo de alumnos fueron:
| Forma de Evaluación | ||
|---|---|---|
| Oral | Escrito | En computadora |
| con desarrollos | ||
| 4 | 2 | 10 |
| 6 | 4 | 8 |
| 7 | 3 | 7 |
| 7 | 6 | 5 |
| 5 | 5 | 7 |
| 4 | 2 | 6 |
| 4 | 3 | 5 |
| 5 | 4 | |
| 6 | 6 | |
| 4 | ||
A partir de estos datos, ¿se puede recomendar, con un nivel de significancia del 5%, alguna técnica de examen en particular?
Solución
Dado que estamos interesados en comparar medias de tres poblaciones distintas, debemos aplicar la prueba de ANOVA. La hipótesis de la prueba viene dada por:
\[\begin{aligned} && H_{0}\!:\; & \quad \mu_{Oral}=\mu_{Esc D}=\mu_{Comp} \nonumber \\ && H_{1}\!:\; & \quad \text{No todas las medias son iguales} \quad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Bajo los siguientes supuestos se puede aplicar la prueba:
Todas las poblaciones involucradas son normales: para constatar que se cumpla, se puede hacer uso de la prueba de Shapiro-Wilk (ver página )
Todas las poblaciones tienen la misma varianza: para verificar este supuesto se puede hacer uso de la prueba de Hartley (ver página )
Las muestras son aleatorias: el cumplimiento de este supuesto se analiza a través de los residuos medidos como \(e_{ij}=x_{ij}-\overline{x}_{j}\)
En este ejemplo sólo verificaremos el supuesto de igualdad de varianzas y supondremos que los otros dos se cumplen.
Primero calcularemos medias y varianzas muestrales.
| Forma de Evaluación | |||
|---|---|---|---|
| Oral | Escrito | En computadora | |
| con desarrollos | |||
| 4 | 2 | 10 | |
| 6 | 4 | 8 | |
| 7 | 3 | 7 | |
| 7 | 6 | 5 | |
| 5 | 5 | 7 | |
| 4 | 2 | 6 | |
| 4 | 3 | 5 | |
| 5 | 4 | ||
| 6 | 6 | ||
| 4 | |||
| Media | 5.20 | 3.57 | 6.44 |
| Varianza | 1.51 | 2.29 | 3.28 |
| Gran media | 5.19 | ||
| n | 26 | ||
| c | 3 | ||
Recordando la hipótesis y el estadístico de la prueba de Hartley (ver página ) tenemos: \[\begin{aligned} H_{0}: \!:\; & \sigma_{Oral}^{2}=\sigma_{Esc D}^{2}=\sigma_{Comp}^{2} \nonumber \\ H_{1}: \!:\; & \text{Alguna varianza es distinta} \qquad \textbf{Prueba lateral derecha} \nonumber \end{aligned}\]
Donde el estadístico de la prueba es el siguiente: \[\begin{aligned} F_{max \quad c,(\overline{n}-1)}\!=\; & \frac{S^{2}_{max}}{S^{2}_{min}} \nonumber \\ F_{max \quad 3,(8-1)}\!=\; & \frac{3.28}{1.51} = 2.17 \end{aligned}\]
La zona de rechazo es: \[\begin{aligned} \textbf{ZR}\!=\; & \lbrace F_{max \quad c,(\overline{n}-1)} \in \mathbb{R} > 0 \quad \vert \quad F_{max \quad c,(\overline{n}-1)}> F_{max \quad c,(\overline{n}-1)}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace F_{max \quad 3,7} \in \mathbb{R} > 0 \quad \vert \quad F_{max \quad 3,7}>6.94 \rbrace \Rightarrow F_{max}^{obs}=2.17 \notin \textbf{ZR} \end{aligned}\]
En conclusión, no tenemos evidencia para rechazar \(H_{0}\) por lo que supondremos que las varianzas son iguales.
Procediendo al cálculo de la suma de los cuadrados entre grupos y dentro de los grupos, tenemos:
\[\begin{aligned} SCE=\sum_{j=1}^{c}r_{j}(\overline{x}_{j}-\overline{\overline{x}})^{2} \end{aligned}\]
| Cuadrados entre grupos | |||
|---|---|---|---|
| Oral | Escrito | En computadora | |
| con desarrollos | |||
| 0.001 | 18.391 | 14.111 | |
| SCE | 32.50 | ||
\[\begin{aligned} SCD=\sum_{j=1}^{c}\sum_{i=1}^{r_{j}}(x_{ij}-\overline{x}_{j})^{2} \end{aligned}\]
| Cuadrados dentro de los grupos | |||
|---|---|---|---|
| Oral | Escrito | En computadora | |
| con desarrollos | |||
| 1.44 | 2.47 | 12.64 | |
| 0.64 | 0.18 | 2.42 | |
| 3.24 | 0.33 | 0.31 | |
| 3.24 | 5.90 | 2.09 | |
| 0.04 | 2.04 | 0.31 | |
| 1.44 | 2.47 | 0.20 | |
| 1.44 | 0.33 | 2.09 | |
| 0.04 | 5.98 | ||
| 0.64 | 0.20 | ||
| 1.44 | |||
| SCD | 53.54 | ||
Luego, calculando el estadístico de la prueba:
\[\begin{aligned} F_{obs}\!=\; & \frac{SCE/(c-1)}{SCD/(n-c)} \nonumber \\ \!=\; & \frac{32.50/(3-1)}{53.54/(26-3)}=6.98 \end{aligned}\]
La zona de rechazo de \(H_{0}\) para \(\alpha=0.05\) es:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace F_{c-1,n-c} \in \mathbb{R} >0 \quad \vert \quad F_{c-1,n-c}>F_{c-1,n-c}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace F_{2,23} \in \mathbb{R} > 0 \quad \vert \quad F_{2,23}>3.42\rbrace \Rightarrow F_{obs}=6.98 \in \textbf{ZR} \end{aligned}\]
Por lo que se rechaza la hipótesis nula, es decir hay evidencia suficiente para afirmar que no todas las medias son iguales. Esto significa que no todas las modalidades de examen final producen idénticos resultados, medidos por las notas finales de dichos exámenes.
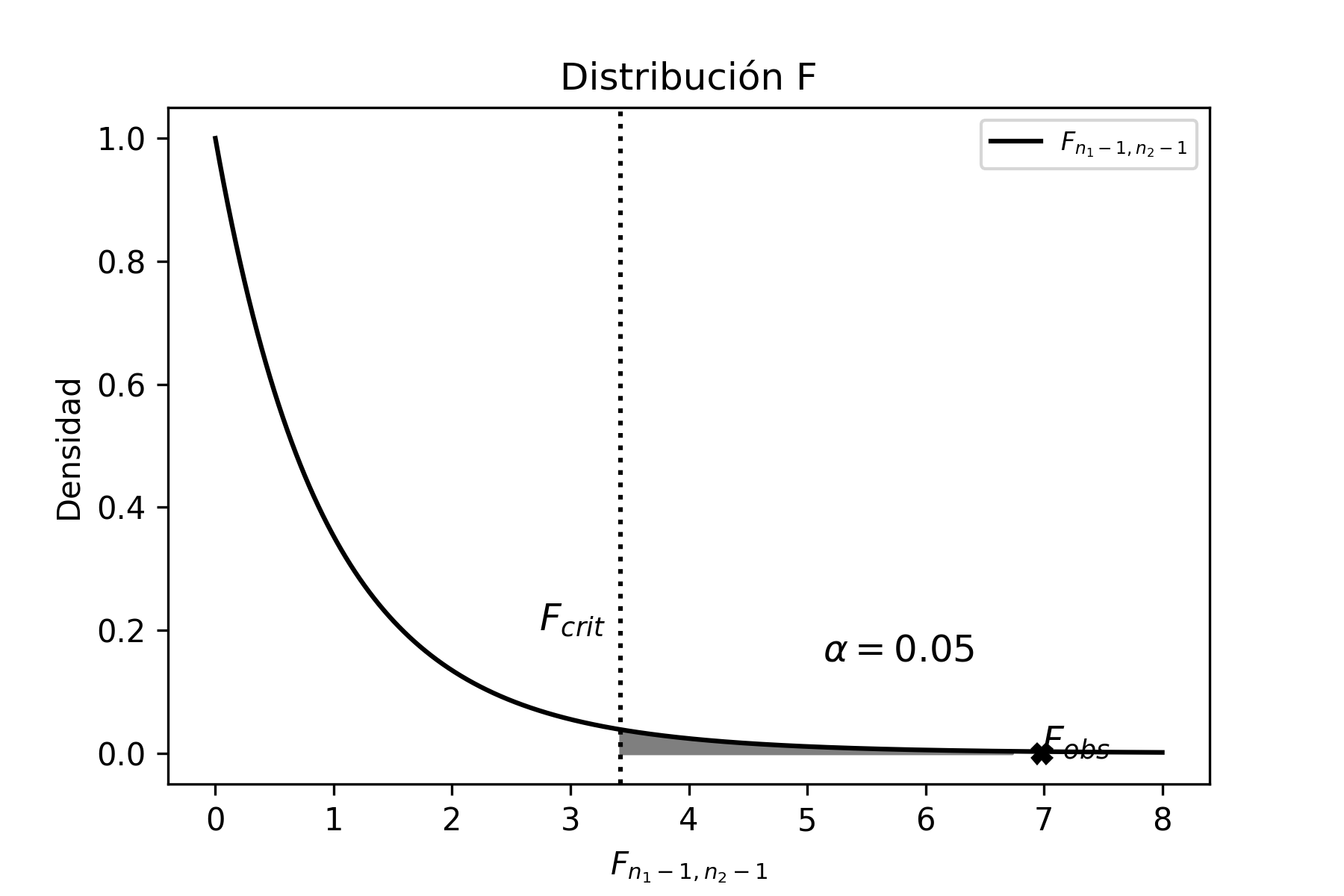
Si construimos la Tabla ANOVA (ver cuadro de la página ), nos queda:
| Variación | Suma de | Grados de | Cuadrados | F | p-valor |
| Cuadrados | Libertad | Medios | |||
| Entre Grupos | \(SCE=32.50\) | \(3-1\) | \(CME=\frac{32.50}{3-1}\) | \(F=6.98\) | \(0.005\) |
| Dentro de los Grupos | \(SCD=53.54\) | \(26-3\) | \(CMD=\frac{SCD}{26-3}\) | ||
| Total | \(SCT=86.04\) | \(26-1\) | \(CMT=\frac{86.04}{26-1}\) | ||
Para poder conocer cuál/cuáles de las medias son diferentes, se usa el estadístico de Tukey-Kramer ([TK]). Resolviendo para un \(\alpha=0.05\) y teniendo en cuenta que, según la tabla, es \(q_{c,n-c,\alpha}=q_{ 3;23;0.05}=3.54\), tenemos: \[\begin{aligned} T_{ij}\!=\; & q_{ c,(n-c),\alpha}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{i}}+\frac{1}{r_{j}}\right)} \nonumber \\ T_{Oral,EscD}\!=\; & q_{3;23;0.05}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{Oral}}+\frac{1}{r_{EscD}}\right)} \nonumber \\ \!=\; & 3.54 \times \sqrt{\frac{2.33}{2}\left(\frac{1}{10}+\frac{1}{7}\right)}=1.87 \nonumber \end{aligned}\] \[\begin{aligned} T_{Oral,Comp}\!=\; & q_{3;23;0.05}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{Oral}}+\frac{1}{r_{Comp}}\right)} \nonumber \\ \!=\; & 3.54 \times \sqrt{\frac{2.33}{2}\left(\frac{1}{10}+\frac{1}{9}\right)}=1.75 \nonumber \\ T_{Comp,EscD}\!=\; & q_{3;23;0.05}\times \sqrt{\frac{CMD}{2}\left(\frac{1}{r_{Comp}}+\frac{1}{r_{EscD}}\right)} \nonumber \\ \!=\; & 3.54 \times \sqrt{\frac{2.33}{2}\left(\frac{1}{9}+\frac{1}{7}\right)}= 1.92 \nonumber \end{aligned}\]
Por último, comparamos el valor absoluto de cada par de diferencias de medias muestrales con el respectivo punto crítico del estimador de la prueba, entonces: \[\begin{aligned} \Big\vert \overline{x}_{Oral}-\overline{x}_{EscD} \Big\vert \!=\; & \Big\vert 5.20 - 3.57 \Big\vert = 1.63 < T_{Oral,EscD}=1.87 \nonumber \\ \Big\vert \overline{x}_{Oral}-\overline{x}_{Comp} \Big\vert \!=\; & \Big\vert 5.20 - 6.44 \Big\vert = 1.24 < T_{Oral,Comp}=1.75 \nonumber \\ \Big\vert \overline{x}_{EscD}-\overline{x}_{Comp} \Big\vert \!=\; & \Big\vert 3.57 - 6.44 \Big\vert = 2.87 > T_{Comp,EscD}=1.92 \end{aligned}\]
En conclusión, las calificaciones medias de la modalidad en Computadora son distintas a la modalidad Escrito con Desarrollo a un nivel de significancia del 5%. Los resultados de la primera son mejores que los de la segunda modalidad
Desarrollando el código en Python para resolver la prueba de ANOVA, tenemos:
# Librerias
import numpy as np
from scipy import stats
from scipy.stats import f
from scipy.stats import f_oneway
def sc(d):
mean=np.mean(d)
n = len(d)
d=(d-mean)**2
scd=d.sum(axis=0)
return scd, n, mean
# Nivel de significancia
alfa=0.05
# Tratamientos
tratamientos=3
# Datos muestrales. Los arreglos deben comenzar en cero y ser consecutivos
data0 = [4,6,7,7,5,4,4,5,6,4]
data1 = [2,4,3,6,5,2,3]
data2 = [10,8,7,5,7,6,5,4,6]
#Suma de cuadrados
scd=0
gmedia=0
N=0
for x in range(tratamientos):
aux=scd
aux2=gmedia
aux3=N
locals()["scd"+str(x)], locals()["n"+str(x)], locals()["media"+str(x)] = sc(locals()["data"+str(x)])
scd=aux+locals()["scd"+str(x)]
gmedia=aux2+locals()["n"+str(x)]*locals()["media"+str(x)]
N=aux3+locals()["n"+str(x)]
gmedia=gmedia/N
sce=0
for x in range(tratamientos):
aux=sce
sce=aux+locals()["n"+str(x)]*(locals()["media"+str(x)]-gmedia)**2
sct=scd+sce
# Cuadrados medios
cmd=scd/(N-tratamientos)
cme=sce/(tratamientos-1)
cmt=sct/(N-1)
# Estadistico y p valor
F_obs=cme/cmd
p_valor = f.sf(F_obs,tratamientos-1,N-tratamientos)
if p_valor > alfa:
conclusion='No se rechaza la hipotesis nula'
else:
conclusion='Se rechaza la hipotesis nula'
print("Tabla ANOVA")
print("=================================================================")
print("Variacion | SC | GL | CM | F | p-valor")
print("-----------------------------------------------------------------")
print("Entre Grupos | ", round(sce,4), " | ", tratamientos-1, " | ", round(cme,4), " | " , round(F_obs,3), " | ", round(p_valor,4))
print("Dentro Grupos | ", round(scd,4), " | ", N-tratamientos, " | ", round(cmd,4))
print("-----------------------------------------------------------------")
print("Total | ", round(sct,4), " | ", N-1, " | ", round(cmt,4))
print("=================================================================")
print(conclusion)
Tabla ANOVA
=================================================================
Variacion | SC | GL | CM | F | p-valor
-----------------------------------------------------------------
Entre Grupos | 32.502 | 2 | 16.251 | 6.982 | 0.0043
Dentro Grupos | 53.5365 | 23 | 2.3277
-----------------------------------------------------------------
Total | 86.0385 | 25 | 3.4415
=================================================================
Se rechaza la hipotesis nulaHay que tener en cuenta que cada grupo debe ser cargado en un arreglo distinto y se debe indicar la cantidad de tratamientos (o grupos) con los que se desea trabajar.
Para resolver la prueba de Tukey-Kramer usamos:
import pandas as pd
import numpy as np
from statsmodels.stats.multicomp import (pairwise_tukeyhsd,
MultiComparison)
# Nivel de significancia
alfa=0.05
# Tratamientos
tratamientos=3
# Datos muestrales (completar con
# np.nan para que todas las columnas tengan la misma dimension)
data0 = [4,6,7,7,5,4,4,5,6,4]
data1 = [2,4,3,6,5,2,3,np.nan,np.nan,np.nan]
data2 = [10,8,7,5,7,6,5,4,6,np.nan]
df = pd.DataFrame()
for x in range(tratamientos):
df['Tratamiento'+str(x)] = locals()["data"+str(x)]
stacked_data = df.stack().reset_index()
stacked_data = stacked_data.rename(columns={'level_0': 'id',
'level_1': 'Tratamiento',
0:'Resultado'})
MultiComp = MultiComparison(stacked_data['Resultado'],
stacked_data['Tratamiento'])
print(MultiComp.tukeyhsd(alpha=alfa).summary())
Multiple Comparison of Means - Tukey HSD, FWER=0.05
===============================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------------------
Tratamiento0 Tratamiento1 -1.6286 0.0986 -3.511 0.2539 False
Tratamiento0 Tratamiento2 1.2444 0.2001 -0.5107 2.9996 False
Tratamiento1 Tratamiento2 2.873 0.003 0.948 4.7981 True
---------------------------------------------------------------Todos los arreglos deben tener la misma dimensión, por lo que, en este caso, se deben completar los faltantes con valores “missing”, es decir con “np.nan”.
Función de Potencia y Curva CO
Definición 4.1. La función de potencia de un test, que simbolizaremos por \(\phi(\theta_{1})\) , es la probabilidad de rechazar la hipótesis nula de que \(\theta=\theta_{0}\) cuando el valor verdadero del parámetro es \(\theta_{1}\), es decir, la probabilidad de rechazar \(H_{0}\) cuando debe ser rechazada.
Sea el contraste paramétrico
\[\begin{aligned} &H_{0}:& \theta = \theta_{0} \nonumber \\ &H_{1}:& \theta = \theta_{1} \nonumber \end{aligned}\] donde \(\theta\) representa al verdadero valor del parámetro poblacional, \(\theta_{0}\) el valor que asume el parámetro poblacional bajo hipótesis nula y \(\theta_{1}\) el valor que asume el parámetro poblacional bajo hipótesis alternativa.
Entonces, se define la función de potencia como:
\[\begin{aligned} \phi(\theta_{1})\!=\; & 1-\beta(\theta_{1})=1-P(\text{Error de Tipo II})=P(\text{Rech $H_{0}\vert H_{0}$ falsa}) \nonumber \\ \!=\; & P(\text{Rech $H_{0}\vert \theta=\theta_{1}$}) \quad \forall \quad \theta_{1} \in \Theta_{1} \end{aligned}\]
Como vemos, \(\phi(\theta_{1})\) nos da la probabilidad de “rechazar cuando efectivamente hay que rechazar”. Veamos un ejemplo para la media poblacional. Sea \(X\) una variable aleatoria que proviene de una población normal con varianza \(\sigma^{2}\) conocida. Suponiendo que estamos ante una prueba de hipótesis con un nivel de significancia \(\alpha\), entonces el estadístico de la prueba es:
\[\begin{aligned} Z=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \nonumber \end{aligned}\]
Si la prueba es del tipo unilateral izquierda, es decir:
\[\begin{aligned} H_{0}: \mu \geq \mu_{0} \nonumber \\ H_{1}: \mu < \mu_{0} \nonumber \end{aligned}\]
Entonces, bajo la hipótesis alternativa \(\mu=\mu_{1}\), la función de potencia vendrá definida por:
\[\begin{aligned} \phi(\mu_{1})\!=\; & 1-\beta(\mu_{1})=P(X \leq X_{crit} \Big\vert E(\overline{X})=\mu_{1}) \nonumber \\ \!=\; & P\bigg(\frac{X-\mu_{1}}{\sigma/\sqrt{n}} \leq \frac{X_{crit}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \nonumber \\ \!=\; & P\bigg(Z \leq \frac{X_{crit}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \end{aligned}\]
Si calculamos la potencia \((1-\beta)\) para distintos valores de \(\mu_{1}\), tenemos el siguiente gráfico:
Por lo tanto, podemos concluir que la función de potencia representa la relación entre los valores de \((1-\beta)\) y los valores de \(\mu_{1}\).
Como se explica más adelante, se considera que una prueba posee una mejor función de potencia cuando su curva tiene una mayor pendiente, dado que indica que el test tiene más capacidad de discriminación, o sea detecta con mayor probabilidad un resultado muestral que no provenga de la población que se está considerando, aún cuando la diferencia entre el estadístico y el parámetro sea pequeña.
Si la prueba es del tipo unilateral derecha, es decir:
\[\begin{aligned} H_{0}: \mu \leq \mu_{0} \nonumber \\ H_{1}: \mu > \mu_{0} \nonumber \end{aligned}\]
Bajo hipótesis alternativa de \(\mu=\mu_{1}\), la función de potencia es:
\[\begin{aligned} \phi(\mu_{1})\!=\; & 1-\beta(\mu_{1})=P(X \geq X_{crit} \Big\vert E(\overline{X})=\mu_{1}) \nonumber \\ \!=\; & P\bigg(\frac{X-\mu_{1}}{\sigma/\sqrt{n}} \geq \frac{X_{crit}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \nonumber \\ \!=\; & P\bigg(Z \geq \frac{X_{crit}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \end{aligned}\]
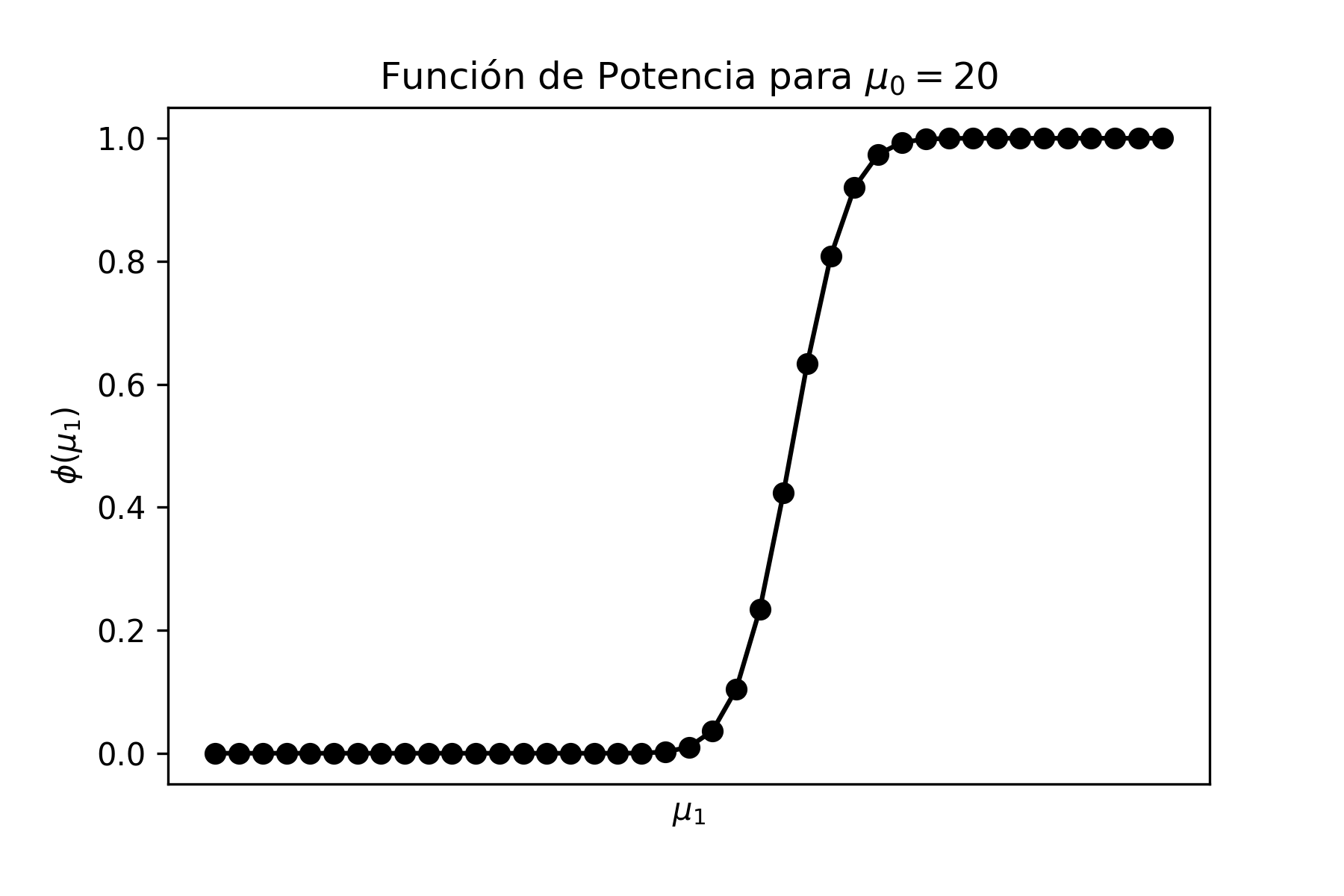
Si la prueba es del tipo bilateral, es decir:
\[\begin{aligned} H_{0}: \mu = \mu_{0} \nonumber \\ H_{1}: \mu \neq \mu_{0} \nonumber \end{aligned}\]
Bajo la hipótesis alternativa de \(\mu=\mu_{1}\), la función de potencia es:
\[\begin{aligned} \label{potencia_bi} \phi(\mu_{1})\!=\; & 1-\beta(\mu_{1})=1-P(X_{crit1} \leq X \leq X_{crit2} \Big\vert E(\overline{X})=\mu_{1}) \nonumber \\ \!=\; & 1-P\bigg( \frac{X_{crit1}-\mu_{1}}{\sigma/\sqrt{n}} \leq \frac{X-\mu_{1}}{\sigma/\sqrt{n}} \leq \frac{X_{crit2}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \nonumber \\ \!=\; & 1-P\bigg( \frac{X_{crit1}-\mu_{1}}{\sigma/\sqrt{n}} \leq Z \leq \frac{X_{crit2}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \end{aligned}\]
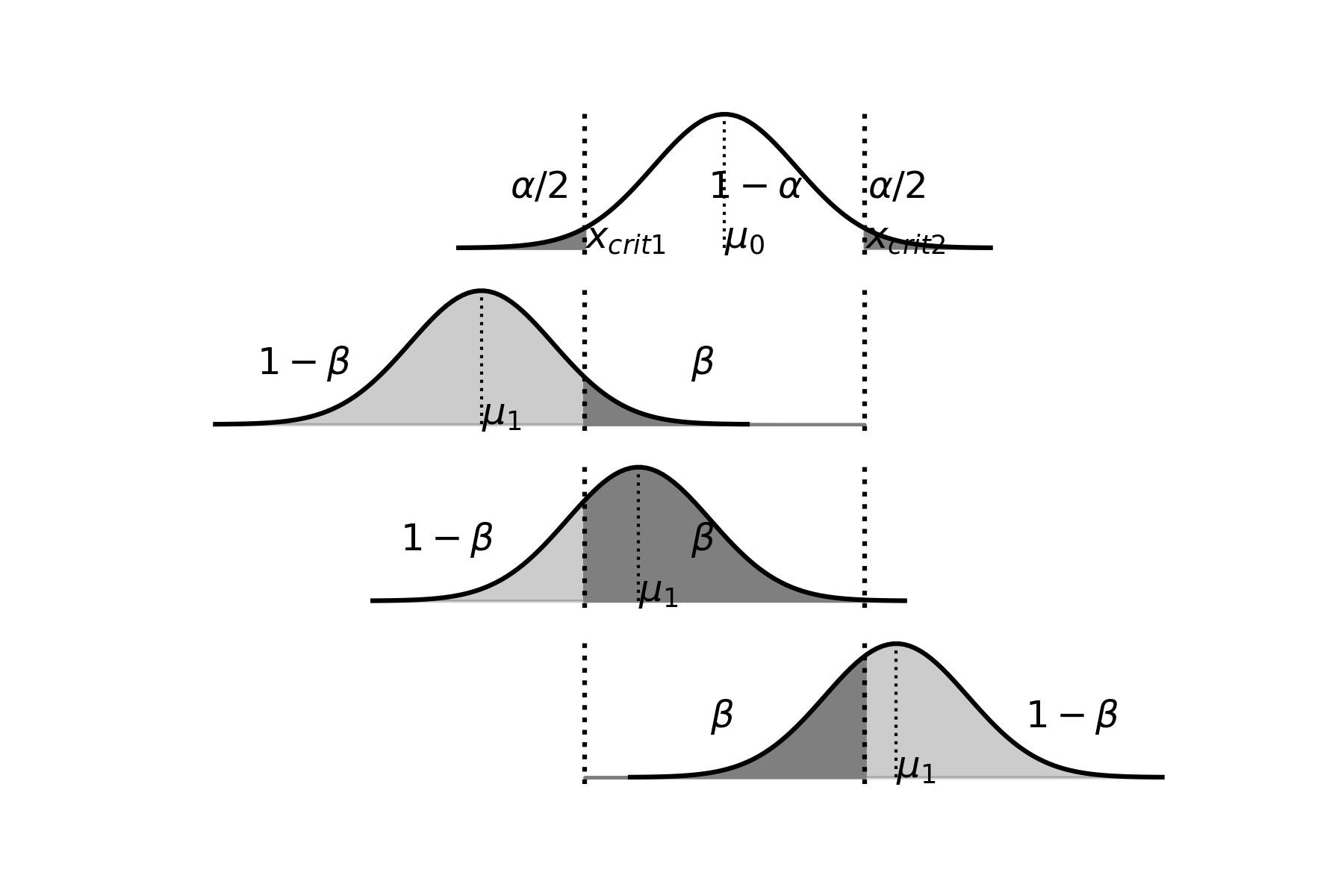
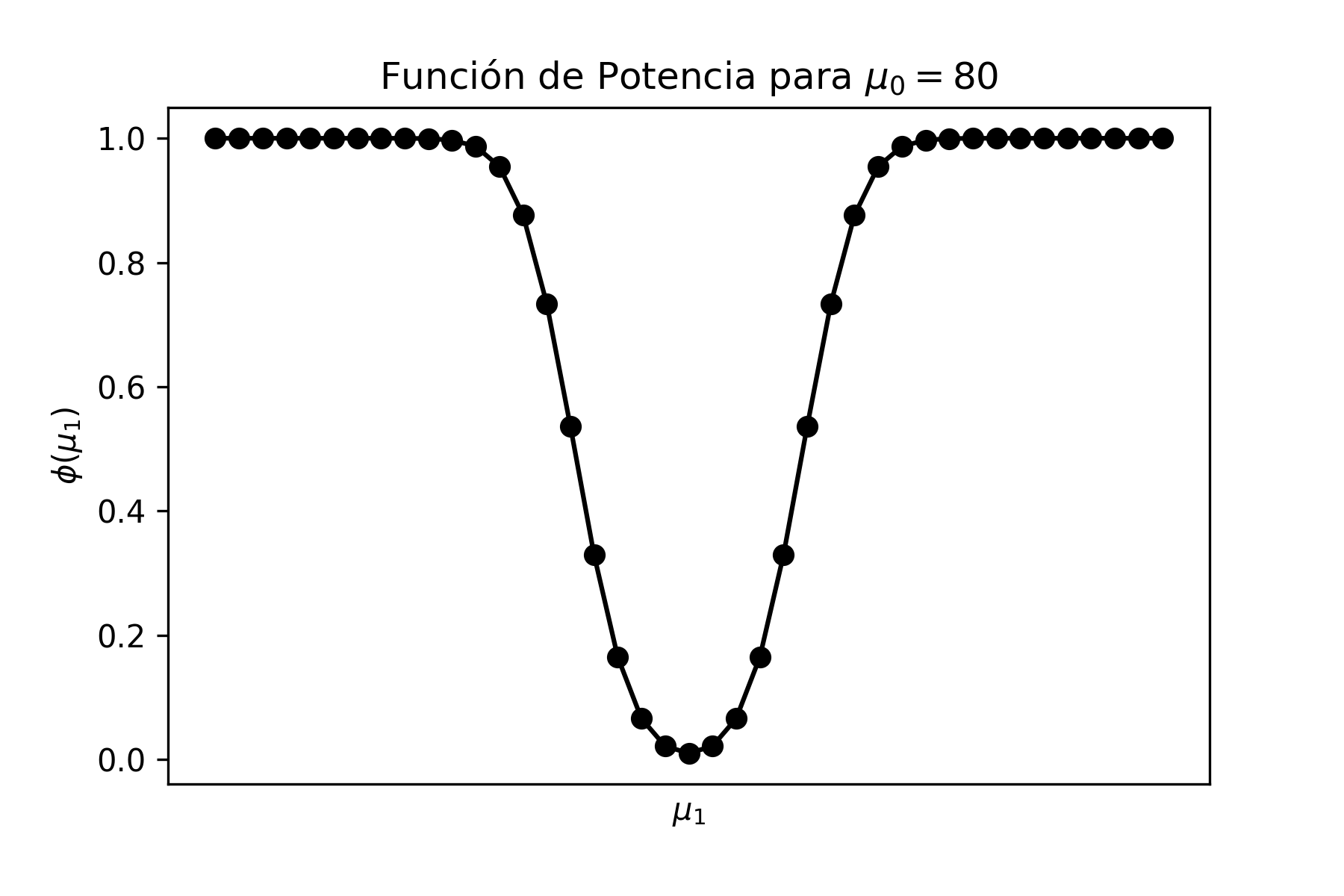
Lo ideal es que esta curva sea lo más cerrada posible en el tramo de convexidad, o sea que las dos ramas posean elevada pendiente (en valor absoluto). De esa forma hay una alta probabilidad de rechazar \(H_{0}\), cuando realmente deba ser rechazada, aunque el valor de \(\mu_{1}\) sea muy próximo a \(\mu_{0}\). Es decir, el test tiene, en ese caso, fuerte sensibilidad para detectar que la media poblacional no es \(\mu_{0}\), a pesar que \(\mu_{1}\) sea cercano a \(\mu_{0}\). Por lo tanto, si queremos comparar dos test de hipótesis que tienen diferente función de potencia, como podrían ser las siguientes figuras:
| Test 1 con (\(\sigma=9\)) | Test 2 con (\(\sigma=3\)) |
 |
 |
se elije la segunda prueba, es decir la de mayor sensibilidad.
La comparación también se puede realizar para distintos tamaños de muestra y en ese caso el resultado es que, a medida que el mismo aumenta, mejora el desempeño del test, es decir, se torna más sensible.
Problema Resuelto 4.8. Los cerámicos producidos por una fábrica poseen una resistencia media a la ruptura de 80 kg con una desviación estándar de 15 kg. Se pretende aplicar un nuevo proceso de fabricación y que el mismo no haga variar la resistencia media. Para ello, se toman 64 cerámicos fabricados por este nuevo proceso. Obtener los valores de la función de potencia para \(\mu=70; 75; 80; 85\) con un \(\alpha=0.01\).
Solución
Como estamos interesados en analizar la resistencia media del cerámico, la cual no queremos que tenga variación frente al nuevo proceso y dado que conocemos la varianza poblacional, podemos plantear las hipótesis de la siguiente manera:
Planteo de hipótesis: \[\begin{aligned} H_{0}: \mu = 80 \nonumber \\ H_{1}: \mu \neq 80 \nonumber \end{aligned}\] cuyo estadístico es:
\[\begin{aligned} Z_{obs}\!=\; & \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \nonumber \end{aligned}\]
Por lo que la función de potencia vendrá dada por la ecuación [potencia_bi], es decir:
\[\begin{aligned} \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{X_{crit1}-\mu_{1}}{\sigma/\sqrt{n}} \leq Z \leq \frac{X_{crit2}-\mu_{1}}{\sigma/\sqrt{n}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \end{aligned}\]
Teniendo en cuenta que estamos trabajando con \(\alpha=0.01\) y usando la relación para estandarizar una variable aleatoria \(Z=(X-\mu)/\sigma\) para la media muestral (ver página ), entonces podemos calcular los puntos críticos \(X_{crit1}\) y \(X_{crit2}\) como:
\[\begin{aligned} X_{crit1}\!=\; & \mu_{0}+Z_{\alpha/2} \sigma /\sqrt{n} \nonumber \\ \!=\; & 80+(-2.57) 15/ \sqrt{64}=75.18 \\ X_{crit2}\!=\; & \mu_{0}+Z_{1-\alpha/2} \sigma /\sqrt{n} \nonumber \\ \!=\; & 80+2.57 \cdot 15/ \sqrt{64}=84.82 \end{aligned}\]
Por lo tanto,
\[\begin{aligned} \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{75.18-\mu_{1}}{15/\sqrt{64}} \leq Z \leq \frac{84.82-\mu_{1}}{15/\sqrt{64}} \Big\vert E(\overline{X})=\mu_{1}\bigg) \end{aligned}\]
Calculando la potencia para los distintos valores de \(\mu_{1}\) se tiene:
\[\begin{aligned} \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{75.18-70}{15/\sqrt{64}} \leq Z \leq \frac{84.82-70}{15/\sqrt{64}} \Big\vert E(\overline{X})=70\bigg) =0.99\nonumber \\ \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{75.18-75}{15/\sqrt{64}} \leq Z \leq \frac{84.82-75}{15/\sqrt{64}} \Big\vert E(\overline{X})=75\bigg) =0.54\nonumber \\ \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{75.18-80}{15/\sqrt{64}} \leq Z \leq \frac{84.82-80}{15/\sqrt{64}} \Big\vert E(\overline{X})=80\bigg) =0.01 \nonumber \\ \phi(\mu_{1})\!=\; & 1-P\bigg( \frac{75.18-85}{15/\sqrt{64}} \leq Z \leq \frac{84.82-85}{15/\sqrt{64}} \Big\vert E(\overline{X})=85\bigg) =0.54 \end{aligned}\]
La función de potencia es:
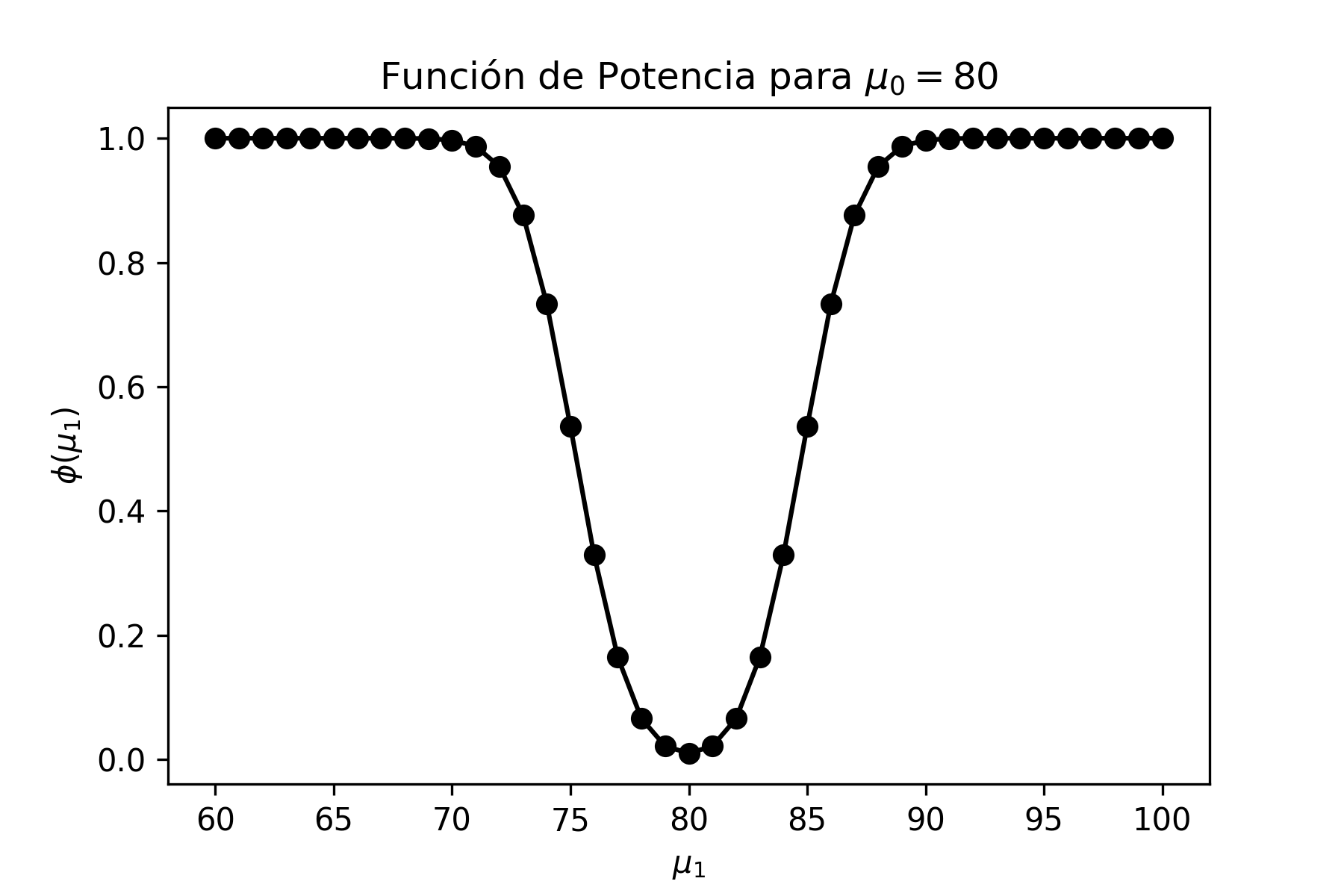
Como conclusión podemos decir que, si la empresa utiliza el nuevo proceso de producción, podrá monitorear si la resistencia media de los nuevos cerámicos se aparta de los 80kg fijados como estándar a mantener. Para ello deberá tomar muestras aleatorias periódicas de 64 cerámicos, con las cuales detectará, con una probabilidad de \(0.54\), cualquier variación de \(\pm 5\)kg en dicha resistencia y con una probabilidad de \(0.99\) cualquier desviación de \(\pm 10\)kg. Todo ello, de acuerdo a la función de potencia obtenida. Por cierto que si deseara tener más sensibilidad (probabilidad más elevada que \(0.54\) y \(0.99\) para la detección de esas desviaciones) debería utilizar muestras de mayor tamaño.
Para obtener la función de potencia con Python, tenemos el siguiente script, donde debemos especificar las medias bajo \(H_{0}\) y \(H_{1}\), \(\sigma\) de la población, el tamaño de la muestra y el tipo de prueba a realizar. Con estas especificaciones, el código nos devuelve la potencia de la prueba. En este ejemplo sólo se calculó, a modo ilustrativo, la potencia para \(\mu_{1}=75\).
#Librerias
import numpy as np
from scipy import stats
from scipy.stats import expon
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import norm
mu, sigma = 0, 1 # media y desvio estandar
normal = stats.norm(mu, sigma)
# Media poblacional bajo hipotesis nula
u0=80
# n muestral
n=64
# Desviacion estandar poblacional
sigma=15
# Nivel de significancia
alfa=0.01
# Media poblacional bajo hipotesis alternativa
u1=75
# Tipo de prueba de hipotesis
tipo=3 # 1: Prueba izquierda 2: Prueba derecha 3: Prueba Bilateral
potencia=pd.DataFrame(np.ones(shape=(1,1)))
def func_pot(alfa,sigma,u0,u1,n):
z=norm.ppf(alfa)
x_crit=u0+z*sigma/n**0.5
z_pot=pd.DataFrame(np.ones(shape=(1,1)))
z_pot=(x_crit-u1)/(sigma/n**0.5)
return z_pot
if tipo==1:
tipo_t="Prueba izquierda"
z_pot=func_pot(alfa,sigma,u0,u1,n)
potencia=1-norm.cdf(z_pot)
elif tipo==2:
tipo_t="Prueba derecha"
z_pot=func_pot(1-alfa,sigma,u0,u1,n)
potencia=1-norm.cdf(z_pot)
elif tipo==3:
tipo_t="Prueba bilateral"
z_pot1=func_pot(alfa/2,sigma,u0,u1,n)
z_pot2=func_pot(1-alfa/2,sigma,u0,u1,n)
potencia=norm.cdf(z_pot1)+(1-norm.cdf(z_pot2))
print(tipo_t)
print("Media bajo H0: ", u0)
print("Varianza poblacional: ", sigma**2)
print("n muestral: ", n)
print("Nivel de significancia: ", alfa)
print("Media bajo H1: ", u1)
print("Potencia: ", potencia)
print("Error de Tipo II: ", 1-potencia)
Prueba bilateral
Media bajo H0: 80
Varianza poblacional: 225
n muestral: 64
Media bajo H1: 75
Nivel de significancia: 0.01
Potencia: 0.5361891685656514
Error de Tipo II: 0.46381083143434865Definición 4.2. La curva CO (característica de operación)13 corresponde a la función de la probabilidad de error de tipo II ante distintos valores del parámetro bajo hipótesis alternativa. En términos simbólicos:
\[\begin{aligned} 1-\phi(\theta_{1})\!=\; & \beta(\theta_{1})=P(\text{Error de Tipo II})=P(\text{No Rech $H_{0}\vert H_{0}$ falsa}) \nonumber \\ \!=\; & P(\text{No Rech $H_{0}\vert \theta=\theta_{1}$}) \quad \forall \quad \theta_{1} \in \Theta_{1} \end{aligned}\]
La curva CO muestra la probabilidad de no rechazar \(H_{0}\), cuando debe ser rechazada, calculada para los distintos valores de \(\theta_{1}\).
Interpretación del p-valor
Para una variable aleatoria \(X\), el del test de hipótesis sobre el parámetro poblacional de la variable a analizar se define según sea el tipo de prueba: unilateral izquierda, unilateral derecha o bilateral.
Definición 4.3. Sea \(X\) una variable aleatoria con distribución conocida.
: el es igual al área bajo la curva desde el extremo de la distribución hasta el valor observado del estadístico de dicha prueba.
Suponiendo que nuestro estadístico sigue una distribución normal estándar, entonces el viene representado gráficamente como:
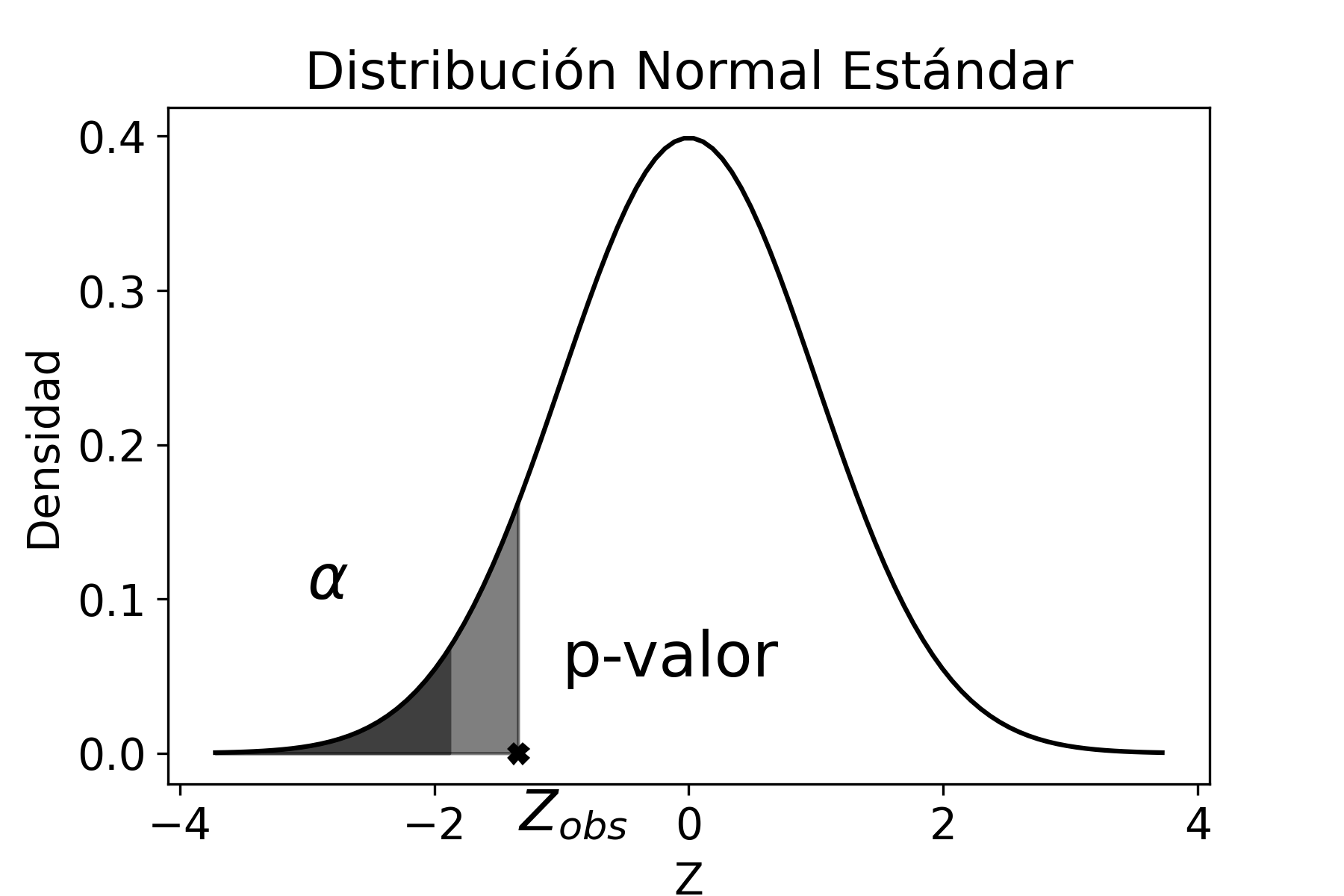
En este ejemplo gráfico, como el p-valor tiene un área mayor que \(\alpha\), es decir que el nivel de significancia, entonces No Rechazaremos \(H_{0}\).
Nótese que el p-valor es la probabilidad acumulada hasta el \(Z_{obs}\), mientras que la probabilidad acumulada hasta el \(Z_{crit}\) corresponde al nivel de significancia \(\alpha\) (o error de tipo I).
: el es igual el área bajo la curva situada en el extremo de la distribución computada a partir del valor observado del estadístico de dicha prueba.
La representación gráfica es:
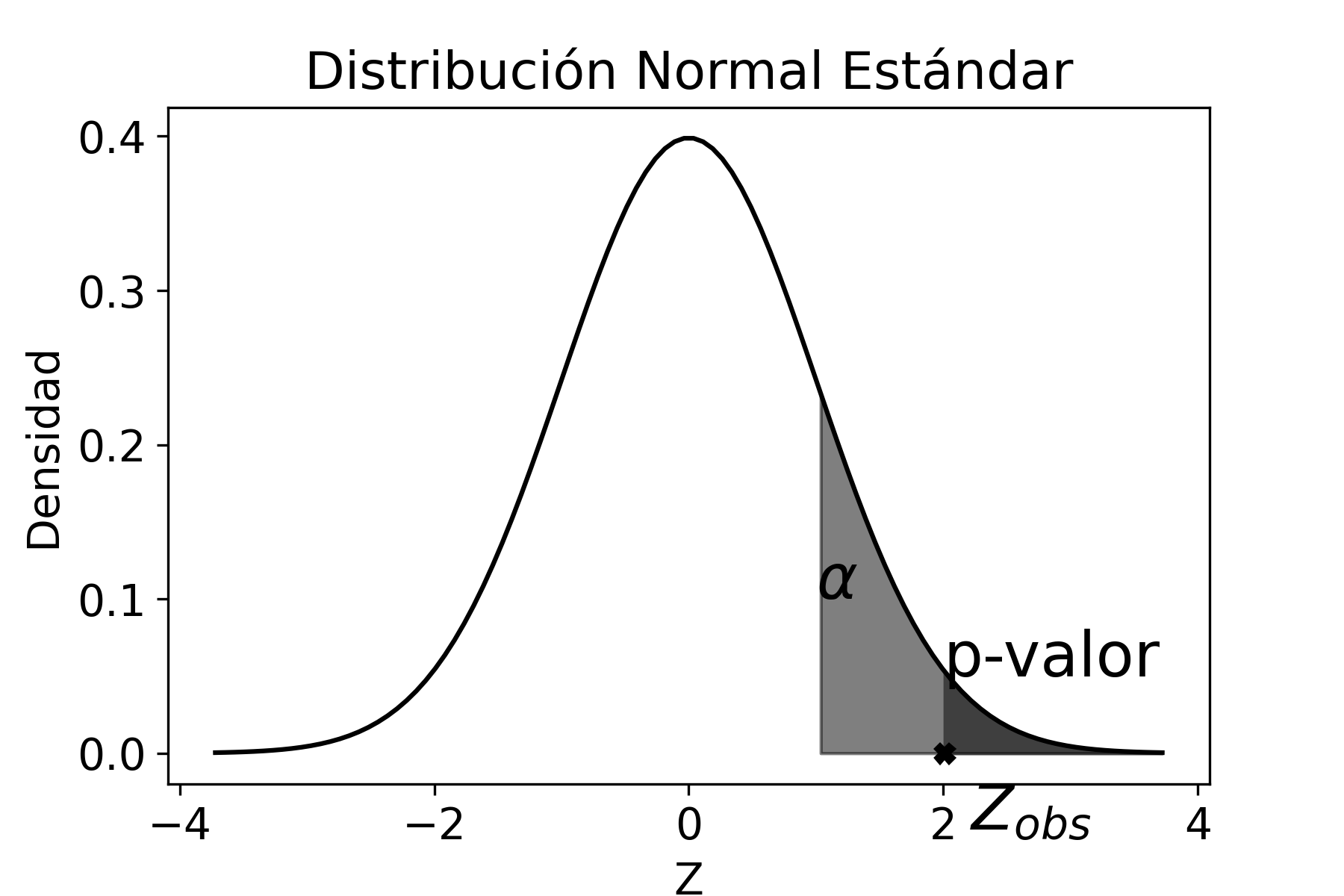
En este caso, como el área correspondiente al p-valor es menor a \(\alpha\), entonces Rechazaremos \(H_{0}\).
: el es igual al área bajo la curva correspondiente al conjunto de valores de \(X\) mayores, en valor absoluto, que el valor observado del estadístico de la distribución.
Gráficamente:
En este último ejemplo, dado que el área del p-valor es menor que \(\alpha\), nuevamente Rechazaremos \(H_{0}\).
En conclusión, la regla de decisión para rechazar o no la hipótesis nula viene dada por:
\[\begin{aligned} \text{p-valor} > \alpha \quad & \Rightarrow &\quad \textbf{No se rechaza }H_{0} \nonumber \\ \text{p-valor} \leq \alpha \quad & \Rightarrow &\quad \textbf{Se rechaza }H_{0} \nonumber \end{aligned}\]
El p-valor para estadísticos que siguen otras distribuciones se calcula de la misma manera.
Prueba de Normalidad de Shapiro-Wilk
Uno de los supuestos que se establece al realizar una prueba de hipótesis es que la variable se distribuye normalmente. El Test de Shapiro Wilk se usa para contrastar la normalidad de un conjunto de datos. Se plantea como hipótesis nula que una muestra \(x_{1},\cdots, x_{n}\) proviene de una población normalmente distribuida. Es decir, \[\begin{aligned} && H_{0}\!:\; & \quad X \sim N(\mu,\sigma^{2}) \nonumber \\ && H_{1}\!:\; & \quad X \nsim N(\mu,\sigma^{2}) \qquad \textbf{Prueba lateral derecha} \nonumber \\ \end{aligned}\]
Para efectuarla se calcula la media \(\overline{X}\) y la varianza muestral \(S^{2}\), y se ordenan las observaciones de menor a mayor. A continuación se calculan las diferencias entre: el primero y el último; el segundo y el penúltimo; el tercero y el antepenúltimo, y así sucesivamente. Posteriormente, se corrigen con unos coeficientes tabulados por Shapiro y Wilk. El estadístico de prueba es:
\[\begin{aligned} W=\frac{D^{2}}{nS^{2}} \end{aligned}\] donde \(D\) es la suma de las diferencias corregidas.
Se rechazará la hipótesis nula de normalidad si el estadístico \(W\) es menor que el valor crítico proporcionado por la tabla elaborada por Shapiro-Wilk para el tamaño muestral y el nivel de significación dado.
En la práctica se suele usar el p-valor de la prueba para tomar la decisión sobre \(H_{0}\).
Problema Resuelto 4.9. Supongamos que queremos analizar si el salario promedio por hora, pagado por las empresas de tecnología, se distribuye normalmente. Para ello se selecciona una muestra aleatoria de 15 empresas y se les consulta el salario promedio que pagan a los trabajadores, medido en dólares, obteniéndose los siguientes resultados:
| Empresa | Salario medio horario (US$) | Empresa | Salario medio horario (US$) |
|---|---|---|---|
| 1 | 14,51 | 9 | 12,37 |
| 2 | 17,31 | 10 | 14,91 |
| 3 | 12,39 | 11 | 17,75 |
| 4 | 15,84 | 12 | 16,28 |
| 5 | 13,51 | 13 | 19,89 |
| 6 | 21,98 | 14 | 20,95 |
| 7 | 13,83 | 15 | 11,85 |
| 8 | 8,13 |
Solución
Cuando estamos interesados en probar la normalidad, como en este caso, vamos a querer “No rechazar \(H_{0}\)”, entonces nos tenemos que concentrar en el error de tipo de II (no rechazar \(H_{0}\) cuando es falsa). Si no tenemos la posibilidad de aumentar el tamaño de muestra, entonces la única alternativa para bajar el error de tipo II es aumentando el error de tipo I, es decir el nivel de significancia \(\alpha\). Es por ello que en pruebas de hipótesis como éstas se sugiere utilizar valores de \(\alpha\) más altos que los habituales. Para este ejemplo utilizaremos un \(\alpha=0.50\).
Hacemos uso del siguiente código para calcular el estadístico de la prueba y luego concluir:
# Libreria
from scipy.stats import shapiro
# Nivel de significancia
alfa=0.50
# Datos muestrales
data=[14.51,17.31,12.39,15.84,13.51,21.98,13.83,
8.13,12.37,14.91,17.75,16.28,19.89,20.95,11.85]
sw_obs, p_value = shapiro(data)
if p_value < alfa:
print("Se rechaza la hipotesis nula")
else:
print("No se rechaza la hipotesis nula")
print("SW observado = ", sw_obs)
print("p valor = ",p_value)
No se rechaza la hipotesis nula
SW observado = 0.9775175452232361
p valor = 0.949718713760376Por lo que no rechazamos la hipótesis nula, y podemos suponer que el salario medio por hora medido en dólares pagado por las empresas de tecnología sigue una distribución normal.
Resumen de Pruebas Paramétricas y No Paramétricas


Nociones de Muestreo
El objetivo de este capítulo es que el lector obtenga los conocimientos básicos sobre Muestreo, las propiedades que deben cumplir las muestras aleatorias, los distintos tipos de muestreo, y el procedimiento para determinar el tamaño de una muestra. Cabe destacar que el tema del muestreo abarca programas completos de materias, ya que es una especialidad dentro de la Estadística, por lo que se deberá complementar con bibliografía adicional en caso de necesitar resolver problemas de mayor complejidad.
Se define a una muestra como un subconjunto extraído de una población, con la intención de realizar inferencia sobre algún parámetro de la población a la cual pertenece.
Una muestra apropiada debe permitir extraer conclusiones válidas y para ello es necesario que reúna las siguientes condiciones:
Homogeneidad: Todos los elementos de la muestra deben provenir de la misma población y la diferencia que exista entre ellos debe ser atribuible al azar.
Independencia: Las observaciones no deben estar mutuamente condicionadas.
Representatividad: La muestra debe ser seleccionada criteriosamente, de forma tal que constituya el mejor reflejo posible de la población.
Además, podemos distinguir entre dos tipos de muestreo:
Muestreo no probabilístico: la selección de los elementos se basa en el juicio personal del observador.
Muestreo probabilístico: todos los elementos de la población tienen una probabilidad conocida de ser elegidos.
En el muestreo probabilístico o aleatorio, se pueden determinar las propiedades de los estimadores, y establecer el error de estimación, mientras que en el muestreo no probabilístico, las propiedades de los estimadores no está asegurada. Es allí donde radica la importancia del muestreo probabilístico.
Existen básicamente cuatro formas de muestreo probabilístico:
Muestreo Aleatorio Simple: Cada unidad de la población tiene la misma probabilidad de ser elegida en la muestra.
Muestreo Sistemático: Se elige aleatoriamente una unidad inicial, y luego se seleccionan las siguientes observaciones a intervalos fijos de orden, tiempo o espacio.
Muestreo Estratificado: Se divide a la población en estratos homogéneos y luego se hace un muestreo aleatorio simple dentro de cada estrato. Se busca que la variación entre estratos sea mayor y que la variación dentro de los mismos, la menor posible.
Muestreo por Conglomerados: Se divide a la población en grupos o conglomerados, y luego se elige una muestra aleatoria simple de conglomerados. Dentro de cada conglomerado seleccionado se toma una muestra aleatoria (puede ser aleatoria simple o sistemática) de los elementos que constituirán las unidades finales de muestreo. Se procura que la variación dentro del conglomerado sea elevada y que la variación entre conglomerados sea la menor posible.
Tamaño de una muestra
Una vez que seleccionamos el método de muestreo, la siguiente pregunta que nos hacemos es: ¿cuál es el tamaño adecuado para una muestra? Para responder a dicha pregunta se debe determinar cuál es el parámetro poblacional principal objeto de nuestro análisis. Generalmente, dichos parámetros, suelen ser la media poblacional o la proporción.
Media poblacional
Comenzaremos analizando el caso en el que nuestro parámetro de interés principal para realizar la inferencia es la media poblacional. Entonces podemos distinguir dos casos: cuando la población es infinita y cuando la población es finita.
Población infinita
Para responder a la pregunta, vamos a suponer que estamos trabajando con una variable cuantitativa, discreta o continua, (\(X\)) y que se desea determinar la media de la población (\(\mu\)), donde además se conoce la varianza poblacional \(\sigma\). Entonces, partiendo de la expresión para un intervalo de confianza sobre la media poblacional (ecuación [ic_z]) podemos escribir: \[\begin{aligned} P\bigg(Z_{\alpha/2}\leq \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq Z_{1-\alpha/2}\bigg)\!=\; & 1-\alpha \end{aligned}\]
Como estamos ante la presencia de la distribución normal estándar que es simétrica respecto a la media, y llamando a \(\vert \overline{X}-\mu \vert\) error de estimación \(e\), podemos escribir: \[\begin{aligned} \label{ec_ic} P\bigg(\vert \overline{X}-\mu \vert < Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \nonumber \\ P\bigg(\vert e \vert < Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\bigg)\!=\; & 1-\alpha \end{aligned}\]
En otras palabras, podemos decir que [ec_ic] es la probabilidad de cometer un error de estimación máximo de \(Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\), en valor absoluto.
Si operamos con la desigualdad contenida dentro del paréntesis de ([ec_ic]) para despejar \(n\), tenemos:
\[\label{n_inf} { n_{\infty} \geq \frac{Z_{1-\alpha/2}^{2}\sigma^{2}}{e^{2}}}\] donde \(n_{\infty}\) representa el tamaño de muestra necesario para que el error deseado de estimación del parámetro no supere el valor \(\vert Z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \vert\).
Cabe destacar que este tamaño de muestra es válido para una población infinita. Si se trabaja con poblaciones finitas y se extrae la muestra sin reemplazo, es necesario realizar correcciones para las varianzas.
Población finita
Partiendo de la inecuación [n_inf] y aplicando el factor de corrección para poblaciones finitas, tenemos que el tamaño de la muestra vendrá dado por:
\[\begin{aligned} n\!=\; & \frac{Z_{1-\alpha/2}^{2}\sigma^{2}}{e^{2}} \frac{N-n}{N-1}\nonumber \\ \!=\; & n_{\infty} \frac{N-n}{N-1} \end{aligned}\]
Despejando \(n\) de la ecuación anterior, llegamos a:
\[\label{n_fin} { n= \frac{n_{\infty} N}{(N-1)+n_{\infty}}}\] donde \(N\) es el tamaño de la población y \(n\) es el tamaño de la muestra con población finita.
Proporción poblacional
Si el parámetro principal de interés que queremos analizar está asociado a una proporción (\(\pi\)), es decir que la variable de interés es cualitativa, entonces el tamaño de la muestra para una población infinita viene dado por:
\[\label{n_p} { n_{\infty} \geq \frac{Z_{1-\alpha/2}^{2}\pi(1-\pi)}{e^{2}}}\]
En el caso de trabajar con una población finita, debemos aplicar el mismo factor de corrección que en el caso de la media poblacional (ver [n_fin]).
Resumiendo, podemos decir que:
\(Z_{1-\alpha/2}\) es un valor que viene de la distribución normal estándar y está asociado a la confianza de la estimación que se realizará. Si la confianza es de un 95%, entonces el valor de \(Z_{1-\alpha/2}\) sera de \(1.96\).
\(\sigma^{2}\) es la varianza poblacional de \(X\) (variable cuantitativa) y \(\pi(1-\pi)\) la varianza poblacional de \(\pi\), que en ambos casos indica si hay mayor o menor dispersión en la población, lo cual incide en el tamaño de la muestra. . Cuando no se conoce \(\sigma^{2}\), es suficiente con tener un valor aproximado para poder determinar el tamaño de muestra14.
\(e\) es el error máximo aceptable, medido en términos de la variable en cuestión si es cuantitativa, o en términos de proporción si es cualitativa (dicotómica). Es decir, si estamos en el caso de una variable medida en pesos, el error se mide en pesos, y si es una proporción se mide en puntos porcentuales
Problema Resuelto 5.1. Se desea conocer si, de acuerdo a los censos nacionales de Población 2010 y 2022, hubo algún cambio en la cantidad promedio de personas que viven en una misma vivienda. En el país había en 2010 un total de \(11.3\) millones viviendas y el promedio de personas por vivienda era de \(3.54\) y la varianza \(0.5\). ¿Cuántas viviendas se deben seleccionar para que, con un nivel de confianza del 95%, podamos estimar el número promedio de personas por vivienda en 2022 con un error absoluto máximo no mayor de \(0.1\) personas por vivienda?
Solución
Teniendo en cuenta que estamos trabajando con una población muy grande y que la variable de interés es la media poblacional, entonces podemos usar la expresión [n_inf]:
\[\begin{aligned} n_{\infty} &\geq & \frac{Z_{1-\alpha/2}^{2}\sigma^{2}}{e^{2}} \nonumber \\ n_{\infty} &\geq & \frac{1.96^{2} 0.5}{0.1^{2}} \simeq 192 \quad \text{viviendas} \end{aligned}\]
O sea que habría que seleccionar al menos 192 viviendas para cumplir con las condiciones impuestas de un error absoluto máximo de \(0.1\) personas y un nivel de confianza del 95%. Como podemos apreciar, en este caso conocemos la varianza en el año 2010 y la utilizamos como aproximación de la varianza en el año 2022 (que desconocemos) para determinar el tamaño de muestra.
Problema Resuelto 5.2. Una compañía de transporte local de pasajeros piensa establecer una línea desde un determinado barrio hasta el centro de la ciudad. Dicha empresa quiere estimar la proporción de usuarios que utilizarían esa nueva ruta, con una confianza del 95% y un error máximo de \(\pm 0.02\) puntos porcentuales. ¿Cuántas personas, sobre una población de 8000 potenciales usuarios, debería entrevistar a fin de tomar la decisión de implementar o no el nuevo servicio? ¿Por qué los valores de \(n_{\infty}\) y \(n\) son diferentes?
Solución
En este caso la variable de interés es la proporción, por lo que se debe trabajar con la inecuación [n_p]. Además, dado que la población “no es muy grande”, debemos corroborar si hay que hacer la corrección por poblaciones finitas (ecuación [n_fin]). Por otra parte, cuando se trabaja con proporciones y no se conoce ningún valor de dicha proporción poblacional de estudios anteriores, se suele usar el valor \(\pi=0.5\) ya que maximiza el valor de \(n_{\infty}\).
Primero aplicamos [n_p]:
\[\begin{aligned} n_{\infty} & \geq & \frac{Z_{1-\alpha/2}^{2}\pi(1-\pi)}{e^{2}} \nonumber \\ n_{\infty} & \geq & \frac{1.96^{2}\cdot 0.5(1-0.5)}{0.02^{2}}\simeq 2\,401 \quad \text{personas} \end{aligned}\]
Una regla que se suele usar para saber si se debe aplicar la corrección por poblaciones finitas es ver si \(n_{\infty}\) supera el 5% del total de la población, entonces se recomienda corregir, caso contrario no efectuar dicha corrección. O sea:
\[\begin{aligned} \frac{n_{\infty}}{N}>0.05 \end{aligned}\] En este caso tenemos que esa relación es \(2401/8000=0.30\) por lo que se recomienda corregir, usando [n_fin]:
\[\begin{aligned} n\!=\; & \frac{n_{\infty} N}{(N-1)+n_{\infty}} \nonumber \\ \!=\; & \frac{2\,401\cdot 8\,000}{(8\,000-1)+2\,401} \simeq 1\,847 \quad \text{personas} \end{aligned}\]
Los valores de \(n_{\infty}\) y \(n\) son diferentes porque hemos aplicado la ecuación [n_fin], donde siempre es \(\frac{N}{(N - 1) + n_{\infty}} \leq 1\). La corrección para poblaciones finitas sirve para obtener un tamaño de muestra menor, manteniendo los mismos objetivos de error máximo absoluto y nivel de confianza. Es importante utilizar dicha corrección, cuando corresponde, porque reduce también los costos de muestreo.
Tamaño de muestra con \(\alpha\) y \(\beta\) fijos
Cuando el objetivo no es estimar un parámetro por intervalos de confianza sino efectuar una prueba de hipótesis, se puede calcular el tamaño de muestra haciendo uso del error de tipo I y el error de tipo II simultáneamente. Supongamos que deseamos fijar la probabilidad de cometer ambos errores, entonces el punto crítico de la distribución bajo las hipótesis nula y alternativa será el mismo. Gráficamente tendríamos:
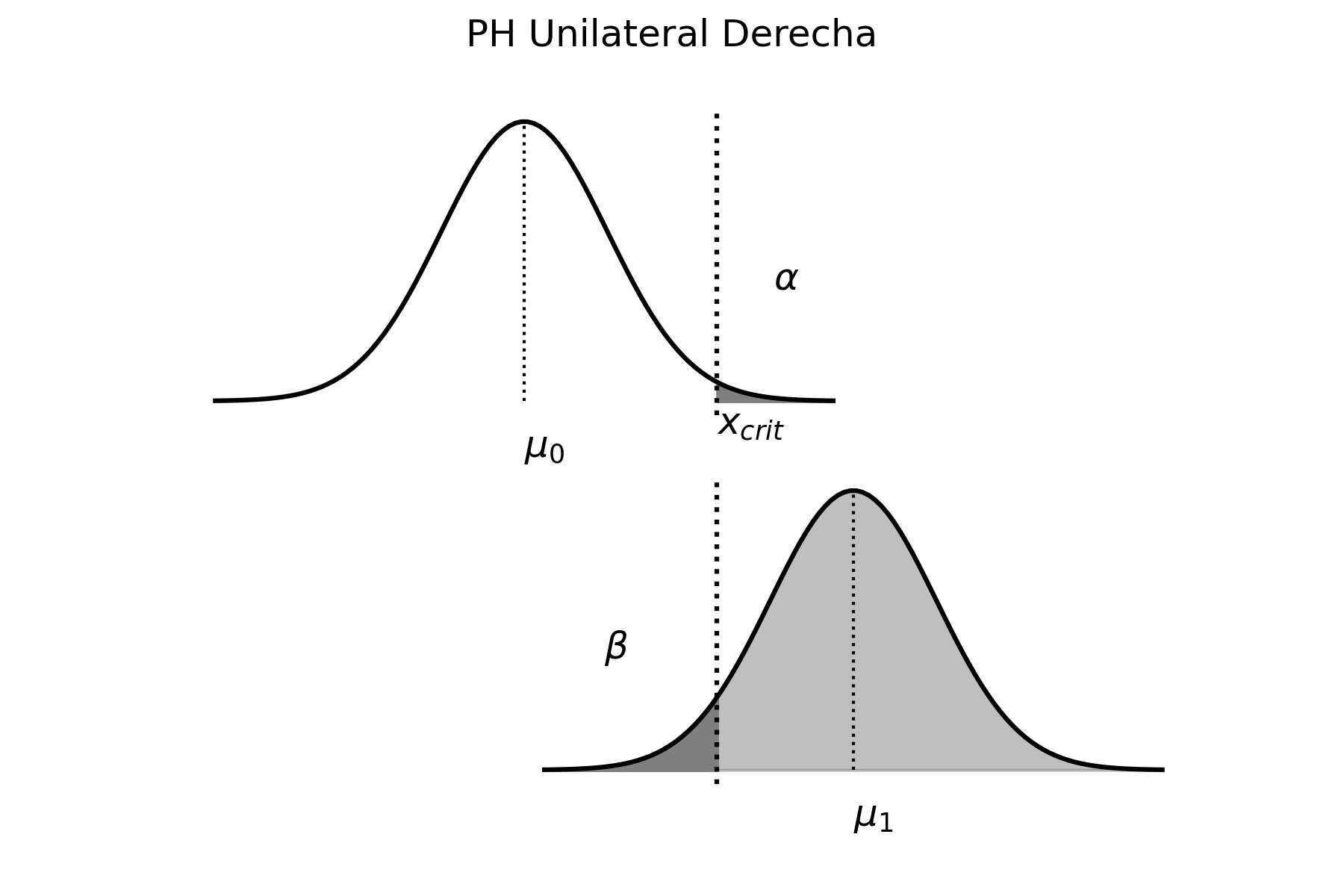
Donde, el punto crítico puede ser escrito para cada distribución de la siguiente manera:
\[\begin{aligned} X_{crit}\!=\; & \mu_{0}+Z_{\alpha}\sigma /\sqrt{n} \nonumber \\ X_{crit}\!=\; & \mu_{1}+Z_{\beta}\sigma /\sqrt{n} \end{aligned}\]
Igualando ambas ecuaciones, dado que los primeros miembros son iguales, y despejando \(n\) llegamos a:
\[\begin{aligned} \label{tam_alfabeta} \mu_{0}+Z_{\alpha}\sigma /\sqrt{n}\!=\; & \mu_{1}+Z_{\beta}\sigma /\sqrt{n} \nonumber \\ (\mu_{0}-\mu_{1})\!=\; & (Z_{\beta}-Z_{\alpha})\sigma /\sqrt{n} \nonumber \\ \sqrt{n}\!=\; & \frac{(Z_{\beta}-Z_{\alpha})\sigma}{(\mu_{0}-\mu_{1})} \nonumber \end{aligned}\] \[{ n=\frac{(Z_{\beta}-Z_{\alpha})^{2}\sigma^{2}}{(\mu_{0}-\mu_{1})^{2}}}\]
En resumen podemos decir que:
El error de tipo II (\(\beta\)), (y en consecuencia la potencia del test), queda automáticamente establecido al fijar el tamaño de la muestra y el error de tipo I (\(\alpha\)).
Para un tamaño de muestra dado, las probabilidades de cometer los errores de tipo I y tipo II están asociadas. Esto significa que, si el error de tipo I se reduce, el error de tipo II aumenta y viceversa.
Si fijamos \(\alpha\) y \(\beta\), debemos determinar el tamaño de la muestra tal que cumpla con esos requerimientos.
Problema Resuelto 5.3. La imprenta de una editorial debe decidir la cantidad de libros a imprimir de la nueva edición. Información archivada de años anteriores indica que se han vendido en promedio \(12\,500\) libros por año, con una desviación estándar de \(1\,735\) libros. Para esta nueva edición, la editorial ha calculado que debe vender \(13\,130\) ejemplares, ya que este nivel le permitiría cubrir costos de impresión y difusión. Ha decidido trabajar con \(\alpha=0.01\) y \(\beta=0.05\). ¿A cuántos potenciales lectores del libro deberá preguntar sobre su intención de compra, para mantener ambos niveles de riesgo?
Solución
En este problema la imprenta se enfrenta a la pregunta de saber si la media poblacional de libros está por encima del valor histórico, para así poder cubrir los costos de impresión. Por lo cuál, la prueba que se plantea es la siguiente:
Prueba de hipótesis: \[\begin{aligned} H_{0}\!:\; & \quad \mu \leq 12\,500 \nonumber \\ H_{1}\!:\; & \quad \mu > 12\,500 \end{aligned}\]
Sabiendo que para mantener el \(\alpha=0.01\) y un \(\beta=0.05\), el tamaño mínimo de muestra debe ser el que viene dado por la ecuación [tam_alfabeta], es decir: \[\begin{aligned} n\!=\; & \frac{(Z_{\beta}-Z_{\alpha})^{2}\sigma^{2}}{(\mu_{0}-\mu_{1})^{2}} \nonumber \\ \!=\; & \frac{(-1.64-2.32)^{2}\cdot 1\,735^{2}}{(12\,500-13\,130)^{2}} \nonumber \\ \!=\; & 119.6\Rightarrow n \geq 120 \end{aligned}\]
En conclusión, con una muestra de por lo menos 120 personas, podremos determinar, con un 1% de nivel de significancia y un error de tipo II del 5%, la cantidad promedio de libros que se venderán.
Gráficamente tenemos las siguientes distribuciones con \(n=120\) y las restricciones de \(\alpha=0.01\), \(\beta=0.05\).
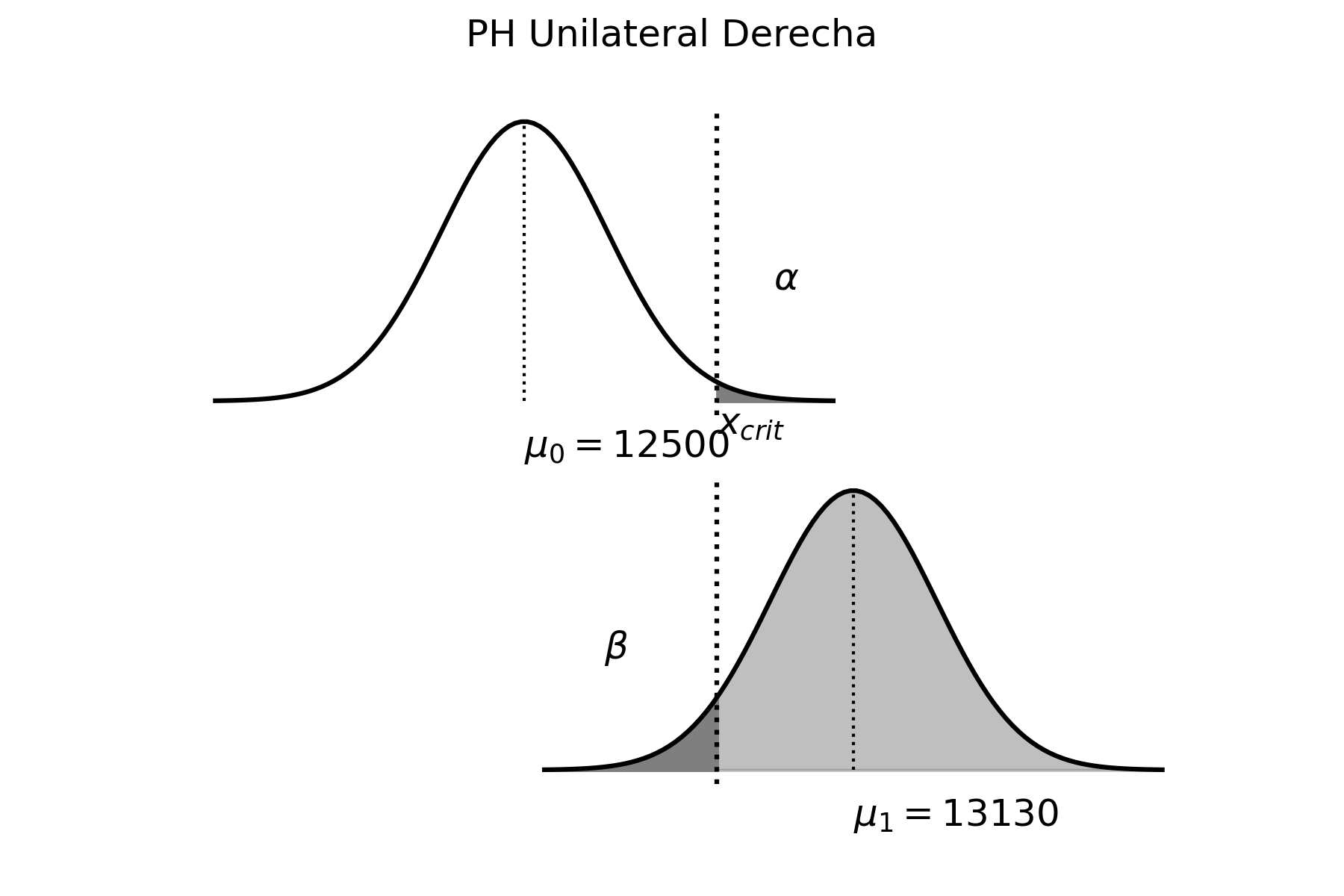
Para calcular con Python el tamaño de la muestra para \(\alpha\) y \(\beta\) fijo, teniendo en cuenta que es una prueba unilateral derecha, se puede usar el siguiente código:
import numpy as np
from scipy import stats
from scipy.stats import norm
alfa=0.01
beta=0.05
sigma=1735
mu0=12500
mu1=13130
normal = stats.norm(0,1)
z_alfa=normal.ppf(1-alfa)
z_beta=normal.ppf(beta)
n=((z_beta-z_alfa)**2*sigma**2)/(mu0-mu1)**2
print("El tamano de la muestra para un alfa ",alfa, " y un beta ", beta, " es: ",n)Tipos de Muestreo
En esta sección se presentarán, de manera sintética, los principales tipos de muestreo, sus características y estimadores.
Muestreo Aleatorio Simple
El muestreo aleatorio simple (MAS) es el más sencillo de implementar. Sin embargo, tiene una restricción muy importante y es que se debe contar con el listado de los elementos que componen toda la población.
Las características principales del MAS son las siguientes:
Cada elemento de la población tiene la misma probabilidad de ser seleccionado
Se necesita un listado de todos los elementos de la población
La selección puede hacerse con o sin reemplazo
La muestra se obtiene a partir de un generador de números aleatorios
Como la probabilidad asignada a cada elemento de la población es la misma, entonces los errores estándares de los estimadores de la media poblacional y proporción poblacional vienen dados por:
| Estimador | Error Estándar | Error Estándar |
| (con reemplazo) | (sin reemplazo) | |
| \(\overline{X}\) | \(\sigma/\sqrt{n}\) | \(\sigma/\sqrt{n} \sqrt{(N-n)/(N-1)}\) |
| \(P\) | \(\sqrt{p(1-p)/n}\) | \(\sqrt{p(1-1)/n} \sqrt{(N-n)/(N-1)}\) |
Hay que tener en cuenta que este método de muestreo no es adecuado en las siguientes ocasiones:
Cuando no es posible enumerar todos los elementos de la población
Cuando la población está formada por subconjuntos bien diferentes entre sí y se necesitan estimaciones para cada subgrupo, además de la estimación general
Si los elementos están muy dispersos geográficamente. En este caso es desaconsejable porque eleva significativamente el costo
Muestreo Sistemático
Este método de muestreo se basa en la forma en que se seleccionan los elementos de la muestra. Se parte de una observación inicial (\(k_{0}\)), la cual es elegida aleatoriamente y es el primer elemento de la muestra. Los elementos sub-siguientes son seleccionados a intervalos \(k\) del punto inicial, es decir, el segundo elemento es el que ocupa el orden \(k_{0}+k\), el tercero el que ocupa el orden \(k_{0}+2k\) y así sucesivamente. El valor de \(k\) vendrá determinado por la relación entre el tamaño de la población y el tamaño de la muestra, es decir:
\[\begin{aligned} k=\frac{N}{n} \end{aligned}\]
Resumiendo, los pasos que se deben seguir en este método de muestreo son:
Decidir el tamaño de la muestra (\(n\)), que se suele determinar en función del presupuesto disponible y del \(n\) que se utilizaría si fuese posible aplicar el MAS
Dividir la población en \(k\) subconjuntos: \(k=N/n\)
Seleccionar al azar un individuo del primer grupo (\(k_{0}\)), para lo cual se toma un número aleatorio entre 1 y \(k\)
Seleccionar los restantes elementos de la muestra tomando el \(k\)-ésimo elemento de cada subconjunto
Una de las grandes desventajas de esta técnica es que no se puede calcular la varianza del estimador, ya que sólo se selecciona al azar la primera observación \(k_{0}\). Por otra parte, en el caso de tener algún conocimiento de que en la población existe cierta periodicidad en el ordenamiento de los elementos, este método puede arrojar muestras sesgadas y se desaconseja su uso.
Muestreo Estratificado
Esta técnica de muestreo divide a la población en subconjuntos llamados estratos. Internamente, dichos estratos tienen baja variabilidad, es decir los elementos que pertenecen al mismo presentan un alto grado de homogeneidad. Sin embargo, la variabilidad entre estratos (calculada a través de la comparación de las medias) es elevada. Posteriormente, se aplica un MAS dentro de cada estrato, resultando en general una muestra con mayor eficiencia que el muestreo aleatorio simple. Otra ventaja que otorga este método es que se puede hacer inferencia respecto a los estratos, es decir acerca de los subconjuntos de la población. Los estratos son mutuamente excluyentes y la unión de todos los estratos es igual a la población.
Entonces, podemos resumir el muestro por estratificación (ME) del siguiente modo:
La población se divide en subconjuntos de acuerdo a alguna característica en común.
Se toma una MAS de cada subgrupo.
Luego, los subconjuntos se combinan en una única muestra para obtener el estimador general.
En general es más eficiente que el MAS (muestras de menor tamaño para un mismo error de estimación).
Es posible diseñar la muestra de tal forma que puedan obtenerse estimaciones respecto de los estratos de la población.
Se combinan las estimaciones para obtener el parámetro general.
Para las estimaciones que se realicen, es posible obtener sus respectivos errores.
Ahora bien, la pregunta que surge es ¿cómo repartimos o sea, asignamos los elementos de la muestra en cada subgrupo o estrato? Para ello existen distintas alternativas que se conocen como métodos de afijación.
Suponiendo que tenemos \(h\) estratos, entonces distinguiremos tres tipos de afijación:
| Igualitaria | Óptima | Proporcional |
|---|---|---|
| \(n_{h}=n/h\) | \(n_{h}=\frac{N_{h}\sigma_{h}}{\sum{N_{i}\sigma_{i}}}n\) | \(n_{h}=\frac{N_{h}}{N}\) |
La afijación igualitaria distribuye de forma equitativa la cantidad de observaciones en cada uno de los estratos, con independencia del tamaño de los mismos. En el caso de la afijación óptima, se distribuye teniendo en cuenta la dispersión dentro de los estratos. Si bien con esta afijación se obtienen los mejores resultados en términos de tamaño de muestra y error, conocer la dispersión dentro del estrato puede ser un obstáculo si no se dispone de información suficiente a la hora de diseñar la muestra. Por último, la afijación proporcional tiene en cuenta la cantidad de observaciones de cada estrato para asignar el tamaño de muestra en dicho subconjunto. Este tipo de asignación suele ser el usado con mayor frecuencia.
Es recomendable no dividir a la población en un número demasiado elevado de estratos, ya que podríamos obtener subconjuntos con un número bajo de elementos que lo integren, con lo cual se reduciría la ganancia que se obtiene con respecto al MAS. Por el motivo opuesto, tampoco es conveniente tomar un número pequeño de estratos.
Media: Estimador y Varianza
El estimador de la media poblacional usando el ME viene dado por:
\[\begin{aligned} \label{media_conglo} \overline{X}=\sum_{h}{w_{h}\overline{X}_{h}} \end{aligned}\] donde \(w_{h}=N_{h}/N\).
Por otra parte, la varianza del estimador en ME viene dada por:
\[\begin{aligned} \label{var_conlgo} V(\overline{X})\!=\; & \sum_{h}{w_{h}^{2}V(\overline{X}_{h})} \\ \nonumber \!=\; & \sum_{h}w_{h}^{2} \frac{\sigma_{h}^{2}}{n_{h}} \end{aligned}\]
Hay que tener en cuenta que, para la varianza del estimador en muestreo aleatorio sin reemplazo, realizado sobre una población finita, se debe aplicar la corrección \(\frac{N_{h}-n_{h}}{N_{h}-1}\).
Efecto Diseño
Para poder comprender si efectivamente el diseño obtenido con el muestreo estratificado es superior al MAS, calculamos la siguiente relación entre las varianzas de los respectivos estimadores: \[\begin{aligned} \text{Efecto Diseño}=\frac{V(\overline{X}_{ME})}{V(\overline{X}_{MAS})} \end{aligned}\]
Si el ratio tiene un valor menor que uno, entonces existe una ganancia utilizando el estimador ME en comparación con MAS.
Problema Resuelto 5.4. Se sabe que en la Zona Sur de nuestra provincia la cosecha proveniente de la soja es almacenada en tres tipos de silos diferentes. Los datos de la siguiente tabla se obtuvieron de la Federación Agraria local:
| Tipo de Silo | Cantidad de silos | \(\sigma_{h}\) (en tn) |
|---|---|---|
| I | 150 | 6,70 |
| II | 500 | 8,30 |
| III | 180 | 3,00 |
Se desea estudiar la capacidad de almacenaje de cada uno de los tres tipos de silos, para lo cual se tomará una muestra de tamaño 96.
Calcular y comparar los \(n_{h}\) utilizando las distintas afijaciones.
Solución
Teniendo en cuenta las afijaciones anteriores, podemos calcular:
| Afijación | |||||
|---|---|---|---|---|---|
| Tipo de Silo | Cantidad de silos | \(\sigma_{h}\) (en tn) | Igualitaria | Proporcional | Óptima |
| I | 150 | 6,70 | 32 | 17 | 17 |
| II | 500 | 8,30 | 32 | 58 | 70 |
| III | 180 | 3,00 | 32 | 21 | 9 |
| Total | 830 | 96 | 96 | 96 | |
donde el denominador de la afijación óptima viene dado por:
\[\begin{aligned} \sum{N_{i}\sigma_{i}}\!=\; & 150\cdot 6.70 + 500 \cdot 8.30 + 180 \cdot 3.00 \nonumber \\ \!=\; & 5\,695 \end{aligned}\]
Con los valores de \(\overline{x}_{h}\) y \(\sigma_{h}\) que arroja la muestra aplicada según la afijación, se obtiene el valor de \(\overline{x}\), aplicando [media_conglo], y de \(V(\overline{x})\) utilizando [var_conlgo].
Muestreo por Conglomerados
En este tipo de muestreo, la población se divide en conglomerados, grupos o “clusters”, donde cada uno es representativo de la población, es decir, posee una variabilidad interna alta, mientras que la variabilidad entre grupos es baja. Generalmente, la creación de los conglomerados está asociada a una distribución espacial, por ejemplo, un grupo de localidades que sean próximas entre sí. Es especialmente útil para reducir costos cuando los elementos de la población están geográficamente dispersos. Su aplicación se realiza a través de los siguientes pasos:
La población se divide en varios conglomerados, cada uno representativo de una parte de la población.
Se realiza un MAS entre los conglomerados de la población.
Se seleccionan muestras aleatorias simples o sistemáticas en cada uno de los conglomerados seleccionados en el punto anterior.
Se combinan las muestras en una única.
Posee las siguientes ventajas e inconvenientes:
Es especialmente indicado cuando las unidades estadísticas (elementos de la población) están muy dispersas geográficamente y llevaría a tener un alto costo si se aplicara MAS sobre todos los elementos de la población.
Es ideal cuando cada conglomerado es muy heterogéneo internamente (varianza alta), y a su vez los conglomerados presentan baja varianza entre sí.
Es también apropiado cuando unos pocos conglomerados representan a una proporción alta de la población.
Una de las desventajas es que puede haber conglomerados importantes que no tienen representatividad en la muestra porque quedaron fuera de la selección MAS del segundo paso.
Media: Estimador y Varianza
Supongamos que tenemos \(K\) conglomerados con \(M\) unidades estadísticas en cada uno (conglomerados iguales), entonces el estimador de la media poblacional es:
\[\begin{aligned} \overline{X}\!=\; & \frac{\sum_{i=1}^{k}\sum_{j=1}^{M} X_{ij}}{kM} \\ \nonumber \!=\; & \sum_{i=1}^{k}\frac{\overline{X}_{i}}{k} \end{aligned}\] donde \(k\) corresponde al número de conglomerados seleccionados en la muestra (o sea que \(k\leq K\)) y \(\overline{X}_{i}\) es la media de cada conglomerado.
La varianza del estimador es:
\[\begin{aligned} V(\overline{X})=\frac{1}{kM}(1-\frac{k}{K}) S^{2}(1+(M-1)^\delta) \end{aligned}\] donde \(\delta\) es el coeficiente de homogeneidad definido como:
\[\begin{aligned} \delta=\frac{\frac{1}{M-1}\sum_{i=1}^{K}\sum_{j,l=1}^{M}(X_{ij}-\overline{X})(X_{il}-\overline{X})}{\sum_{i=1}^{K}\sum_{j=1}^{M}(X_{ij}-\overline{X})} \quad \text{con } j<l \end{aligned}\]
Proporción: Estimador y Varianza
Supongamos nuevamente que tenemos \(K\) conglomerados con \(M\) unidades estadísticas en cada uno (conglomerados iguales), sabiendo que el parámetro poblacional es:
\[\begin{aligned} \pi=\frac{\sum_{i=1}^{K}\sum_{j=1}^{M}{X_{ij}}}{KM} \end{aligned}\] entonces, el estimador usando esta técnica de muestreo viene dado por:
\[\begin{aligned} P=\frac{\sum_{i=1}^{k}\sum_{j=1}^{M}{X_{ij}}}{kM} \end{aligned}\] y su varianza es:
\[\begin{aligned} V(P)=\frac{1}{k}(1-k/K)\frac{\sum_{i=1}^{k}{(P_{i}-P)^{2}}}{k-1} \end{aligned}\] donde \(P_{i}\) es la proporción de éxitos en el conglomerado i-ésimo.
Si los conglomerados son parecidos entre si, es decir, hay baja variabilidad entre grupos, entonces \(P_{i} \to P\) y la varianza del estimador tenderá a cero.
Resumiendo los distintos tipos de muestreo, podemos decir, en general, que:
El MAS es el más sencillo de aplicar si se dispone de un listado completo de los elementos de la población, pero puede ser costoso cuando los elementos que resultan seleccionados son difíciles de acceder (por ejemplo muy dispersos territorialmente).
El ME posibilita mejor la representación de los individuos de toda la población.
El Muestreo por Conglomerados es el que se puede implementar con menor costo, especialmente cuando se trata de muestras de elementos distribuidos en un territorio. Sin embargo, es menos eficiente, ya que necesita muestras más grandes para lograr el mismo nivel de precisión que el ME.
En la práctica, se suele usar una combinación de varias métodos de muestreo.
Análisis de Regresión
El análisis de regresión es el proceso en el cual se propone una relación funcional entre una variable dependiente y una o varias variables independientes, y luego se estiman los coeficientes correspondientes a dicha relación funcional. Hallar la relación funcional y las variables independientes que intervienen en la misma es la parte fundamental en el análisis de regresión.
Abordaremos dos aspectos íntimamente ligados, que son la correlación y el análisis de regresión entre variables. En el primero, analizaremos el grado de asociación que pueden tener las variables objeto de estudio, y en el segundo, cómo se pueden relacionar funcionalmente dichas variables.
Análisis de Correlación
El objetivo del análisis de correlación es medir el grado de asociación que existe entre dos o más variables. Consideremos sólo el caso de dos variables. El primer paso para explorar la posible vinculación entre dos variables es mediante un diagrama de dispersión.
Supongamos que queremos analizar la vinculación entre el peso y la estatura de cada persona, entonces un gráfico de dispersión sería:
Una alternativa es estudiar el grado de asociación conjunta, o de covarianza, que existe entre las dos variables. La covarianza es definida como:
Definición 6.1 (Covarianza). Sean dos variables aleatorias \(X\) y \(Y\), la covarianza es un valor que indica el grado de asociación entre dichas variables medido como:
\[\begin{aligned} \label{cov} Cov \left(X,Y \right)\!=\; & \frac{\sum_{i=1}^{n}{\left( X_{i}-\overline{X}\right) \left( Y_{i}-\overline{Y}\right)}} {n-1}, \qquad \text{para la muestra} \nonumber \\ COV \left(X,Y \right)\!=\; & E(\left( X_{i}-E(X)\right) \left( Y_{i}-E(Y)\right)), \qquad \text{para la población} \end{aligned}\] donde \(\mu_{x}\) y \(\mu_{y}\) son las medias poblacionales de las variables \(X\) e \(Y\) respectivamente.
El signo de la covarianza indica el tipo de asociación entre las dos variables y el valor absoluto representa el grado de asociación entre \(X\) e \(Y\). Si la covarianza es nula, significa que las variables no covarían, es decir, cuando una varía la otra no responde, por lo que son independientes.
Si operamos sobre la expresión de la covarianza muestral y aplicamos las propiedades de la sumatoria, llegamos a:
\[\begin{aligned} \label{covar_alternativa} Cov \left(X,Y \right)\!=\; & \frac{\sum_{i=1}^{n}{\left( X_{i}-\overline{X}\right) \left( Y_{i}-\overline{Y}\right)}} {n-1} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}{\left(X_{i}Y_{i}+X_{i}\overline{Y}-\overline{X}Y_{i}+\overline{X}\overline{Y}\right)}}{n-1} \nonumber \\ \!=\; & \sum_{i=1}^{n}\frac{X_{i}Y_{i}}{n-1}+\sum_{i=1}^{n}\frac{X_{i}\overline{Y}}{n-1}-\sum_{i=1}^{n}\frac{\overline{X}Y_{i}}{n-1}+\sum_{i=1}^{n}\frac{\overline{X}\overline{Y}}{n-1} \nonumber \\ \!=\; & \sum_{i=1}^{n}\frac{X_{i}Y_{i}}{n-1}+\frac{n\overline{X}\overline{Y}}{n-1}-\frac{\overline{X}\overline{Y}n}{n-1}+\sum_{i=1}^{n}\frac{\overline{X}\overline{Y}}{n-1} \nonumber \\ \!=\; & \frac{1}{n-1}\Big(\sum_{i=1}^{n}X_{i}Y_{i}+n\overline{X}\overline{Y}\Big) \end{aligned}\]
Ésta es otra forma de expresar la covarianza entre dos variables que usaremos más adelante.
En términos prácticos, la covarianza es una cantidad bastante difícil de interpretar, ya que por un lado tiene las unidades de medida de \(X\) e \(Y\), y por otro no es simple entender qué expresa concretamente su valor, además de que puede asumir valores entre \(-\infty\) y \(+\infty\).
Para salvar estos inconvenientes se calcula una magnitud denominada coeficiente de correlación lineal, que se determina sobre la base de una relación lineal entre las variables \(X\) e \(Y\). Ésta es otra opción para estudiar el grado de asociación conjunta entre las variables.
Definición 6.2 (Coeficiente de Correlación Lineal). Es una medida adimensional que cuantifica la relación lineal entre dos variables y se calcula como:
\[\begin{aligned} \label{coef_correl} r=\frac{Cov \left(X,Y\right)}{S_{X}S_{Y}}, \qquad \rho=\frac{COV \left(X,Y\right)}{\sigma_{X}\sigma_{Y}} \end{aligned}\] donde \(\rho\) denota al parámetro poblacional y \(r\) al estimador muestral.
Como vemos, el Coeficiente de Correlación Lineal se calcula
dividiendo la covarianza por el producto de los desvíos estándar de
ambas variables, con lo que se obtiene un valor sin unidad de medida que
queda acotado entre \(-1\) y \(1\).
Si el coeficiente de correlación tiende a uno en valor absoluto, indica
un fuerte grado de asociación entre las variables. En cambio, cuando
tiende a cero, existe un débil grado de asociación. En caso de ser
positivo, la asociación es directa, mientras que cuando es negativo la
asociación es inversa. En todos estos casos estamos suponiendo una
relación lineal entre las variables.
| Asociación directa | Asociación Inversa | Sin Asociación |
 |
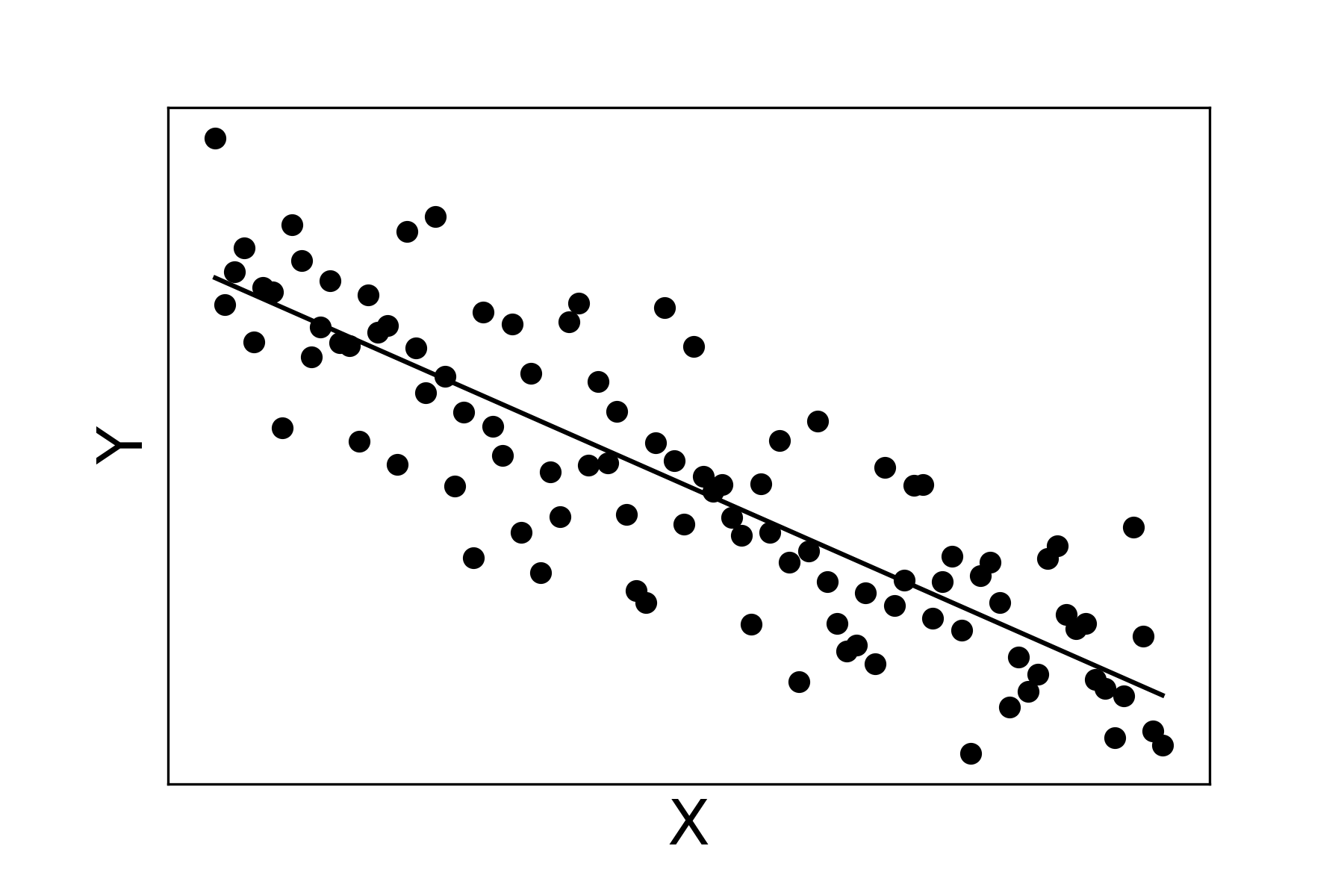 |
 |
Problema Resuelto 6.1. Se dispone de datos de una encuesta realizada a \(13\,378\) personas, que contiene información de la estatura (medida en cm) y peso (medido en kg) de cada una. Se desea conocer el grado de asociación entre dichas variables, conociendo que:
| Variable | Media | Desviación estándar | \({\sum_{i=1}^{n}{\left( x_{i}-\overline{x}\right) \left( y_{i}-\overline{y}\right)}} \) |
|---|---|---|---|
| Estatura (cm) | 163,59 | 9,18 | 796 400,23 |
| Peso (kg) | 71,67 | 13,31 |
Solución
Usando los datos proporcionados en la tabla anterior y la expresión [cov], calculamos la covarianza entre la estatura y el peso:
\[\begin{aligned} Cov \left(X,Y \right)\!=\; & \frac{\sum_{i=1}^{n}{\left( x_{i}-\overline{x}\right) \left( y_{i}-\overline{y}\right)}} {n-1} \nonumber \\ \!=\; & \frac{796\,400,23 \quad \textbf{kg $\times$ cm}}{13\,378-1}=59,53 \quad \textbf{kg $\times$ cm} \end{aligned}\]
Como vemos, la unidad de medida de la \(Cov(X,Y)\), en este caso, es \(kg \times cm\), que es difícil de interpretar y, especialmente, imposible de comparar con la covarianza de otras variables, expresadas en distintas unidades de medida.
Utilizamos entonces, el coeficiente de correlación \(r\) que incorpora los desvíos estándares: \[\begin{aligned} r\!=\; & \frac{Cov \left(X,Y\right)}{S_{X}S_{Y}} \nonumber \\ \!=\; & \frac{59,53 \quad \textbf{kg $\times$ cm}}{9,18 \quad \textbf{kg} \times 13,31 \quad \textbf{cm}}=0,487 \end{aligned}\]
Por lo que, en este ejemplo, existe una asociación positiva entre la estatura y el peso de las personas.
En un caso real es poco probable que el coeficiente de correlación sea exactamente igual a uno. También sería muy raro que el valor de \(r\) sea exactamente cero, indicando total ausencia de asociación lineal entre las variables. Pero siempre surge la pregunta sobre ¿cuál es el verdadero valor del parámetro poblacional? Es por ello que se plantea la necesidad de decidir hasta qué punto se puede pensar que el \(r\) no es significativamente distinto de cero y, por lo tanto, si las variables están o no relacionadas. Se trata de plantear una prueba de hipótesis donde:
\[\begin{aligned} && H_{0}: \rho=\rho_{0}\nonumber \\ && H_{1}: \rho \neq \rho_{0} \qquad \textbf{Prueba bilateral} \nonumber \end{aligned}\]
El estadístico de la prueba es el siguiente: \[\begin{aligned} \frac{r-\rho_{0}}{\sqrt{\frac{1-r^{2}}{n-2}}} \sim t_{n-2} \end{aligned}\]
El caso más usual es cuando se prueba \(\rho_{0}=0\), ya que si se rechaza \(H_{0}\), entonces \(\rho \neq 0\), por lo que existe asociación entre las variables analizadas, condición necesaria para poder seguir con el análisis de regresión.
Análisis de Regresión
El análisis de regresión tiene como objetivo estimar la relación funcional que vincula a una variable dependiente (\(Y\)) con una o varias variables independientes (\(X\)). En este caso, una o más variables/s explica/n el comportamiento estadístico de la otra.
Existen distintos tipos de regresión:
Regresión Simple: se relaciona una variable dependiente con una sola variable independiente. \[\begin{aligned} Y=f\left(X, \epsilon \right) \end{aligned}\]
Regresión Múltiple: se relaciona una variable dependiente con dos o más variables independientes. \[\begin{aligned} Y=f\left( X_{1},X_{2}, \cdots ,X_{n} , \epsilon \right) \end{aligned}\]
A su vez, cada uno de estos tipos de regresiones pueden ser:
Regresión Lineal: la función es lineal respecto a sus parámetros que en el caso de la regresión simple es: \[\begin{aligned} Y=\beta_{0} + \beta_{1} X + \epsilon \end{aligned}\]
Regresión No Lineal: la función no es lineal respecto a alguno de sus parámetros. Por ejemplo, para la regresión simple: \[\begin{aligned} Y=\alpha \beta^{X}+ \epsilon, \qquad Y=\alpha X^{\beta}+ \epsilon \end{aligned}\]
Como veremos, la ecuación de regresión poblacional es un modelo que describe la dependencia del valor promedio (media condicional) de una variable sobre la otra. En el caso de modelos lineales simple, esa relación corresponde a una linea recta.
Regresión Lineal Simple
Supongamos que tenemos una variable \(Y\) (dependiente o respuesta) y otra variable \(X\) (independiente, explicativa o regresor). La relación funcional que se propone para el modelo poblacional viene dada por:
\[\begin{aligned} \label{ec_lineal_simple} Y_{i}\!=\; & \underbrace{\beta_{0}+\beta_{1} X_{i}} + \epsilon_{i} \qquad \forall i\\ && \quad \mu_{YX} \nonumber \end{aligned}\] donde \(\epsilon_{i}\) es el término de error aleatorio. Este término recoge el efecto aleatorio de las \(k\) variables no incluidas en el modelo propuesto, que se suponen son independientes de \(X\), y no autocorrelacionadas15. Como consecuencia del TCL, la suma de las \(k\) variables aleatorias tiende a distribuirse normalmente con media cero y varianza constante (homocedasticidad), a medida que la cantidad de variables omitidas \(k\) crece, es decir:
\[\begin{aligned} \epsilon \sim N(0,\sigma^{2}) \end{aligned}\]
Si hacemos la representación gráfica de la ecuación [ec_lineal_simple] obtenemos:
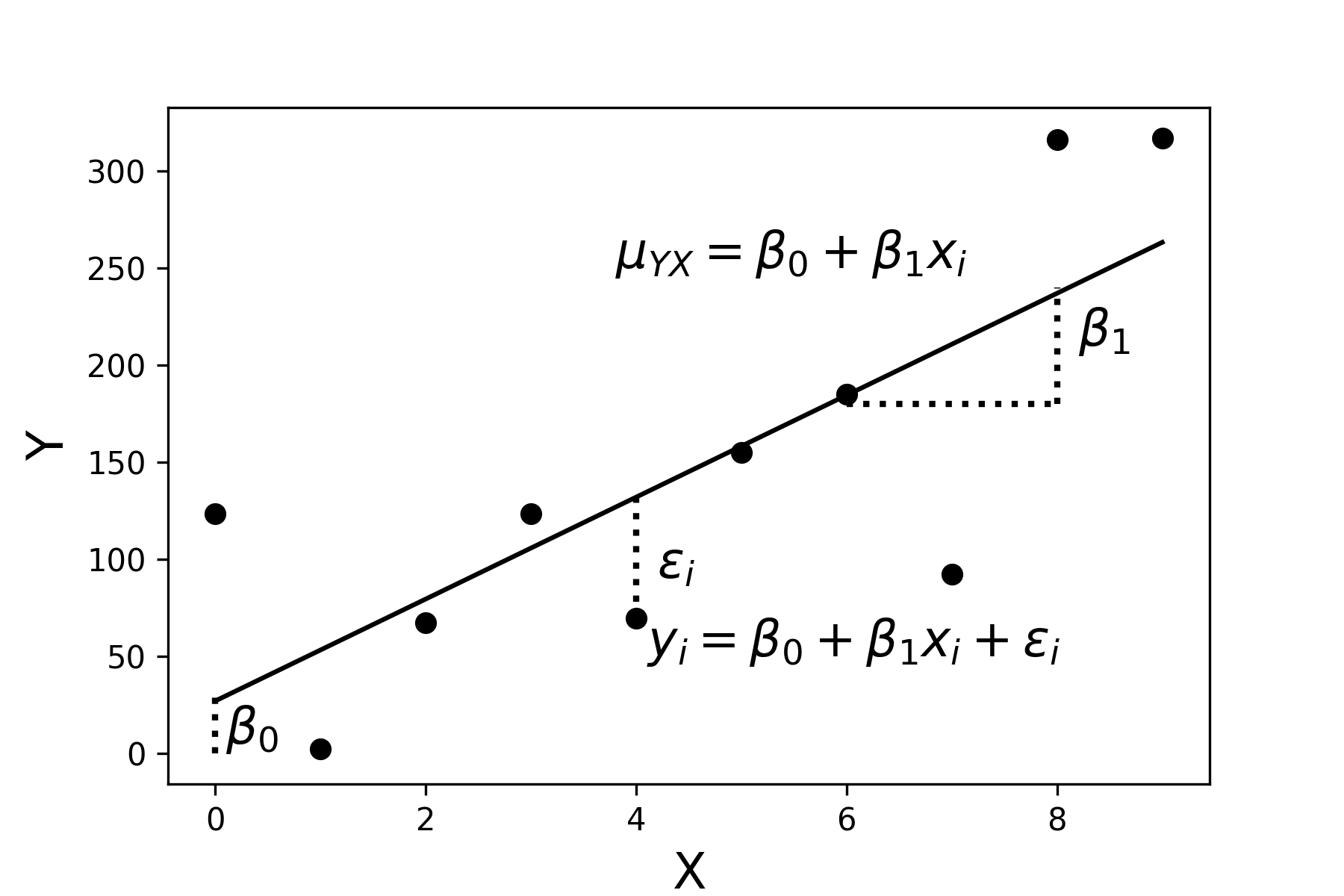
Podemos escribir los valores de \(\beta_{o}\) y de \(\beta_{1}\) como:
\[\begin{aligned} \beta_{0}\!=\; & E(Y\vert X=0) \\ \beta_{1}\!=\; & \frac{\partial E(Y\vert X)}{\partial X} \end{aligned}\] es decir que \(\beta_{0}\) es el valor promedio de \(Y\) cuando el valor \(X\) es cero; y \(\beta_{1}\) mide el cambio en el valor promedio de \(Y\) como resultado de un cambio unitario de \(X\).
Sin embargo, en pocas ocasiones vamos a contar con todos los datos de la población para poder encontrar \(\beta_{0}\) y \(\beta_{1}\), por lo que debemos obtener una recta estimada a partir de los datos de una muestra.
Es decir, se obtienen coeficientes del modelo que no son exactamente los mismos que los coeficientes poblacionales, simplemente porque estamos trabajando con un subconjunto de la población. En el siguiente gráfico, se muestra un ejemplo en donde la recta estimada con los datos muestrales difiere de la recta poblacional (que es desconocida).
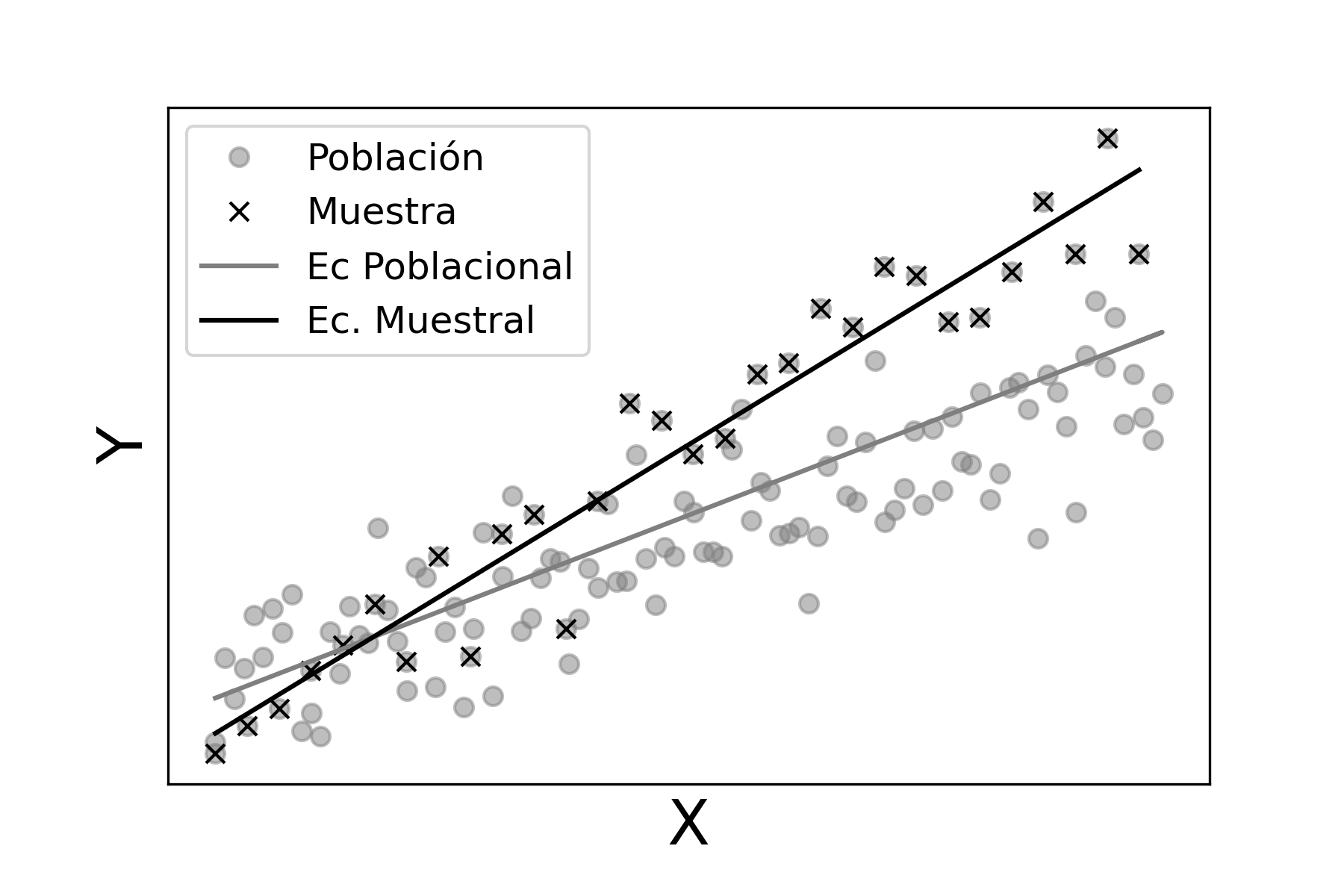
La recta de regresión muestral provee una estimación de la recta poblacional y permite formular los pronósticos de la variable \(Y\), mediante la cuantificación de la relación entre las variables.
La recta de regresión muestral puede expresarse como:
\[\begin{aligned} \label{ecaucion_muestra} Y_{i}\!=\; & \underbrace{b_{0}+b_{1} X_{i}} + e_{i} \\ && \quad \widehat{Y} \nonumber \end{aligned}\] donde \(e_{i}\) ahora representa al residuo del modelo, \(b_{0}\) y \(b_{1}\) son los estimadores de los parámetros poblacionales \(\beta_{0}\) y \(\beta_{1}\) respectivamente, y \(\widehat{Y}\) corresponderá a la predicción obtenida con el modelo.
La diferencia entre la recta poblacional y la recta de regresión que, suponemos, hemos determinado con la muestra, la podemos observar en el siguiente gráfico:
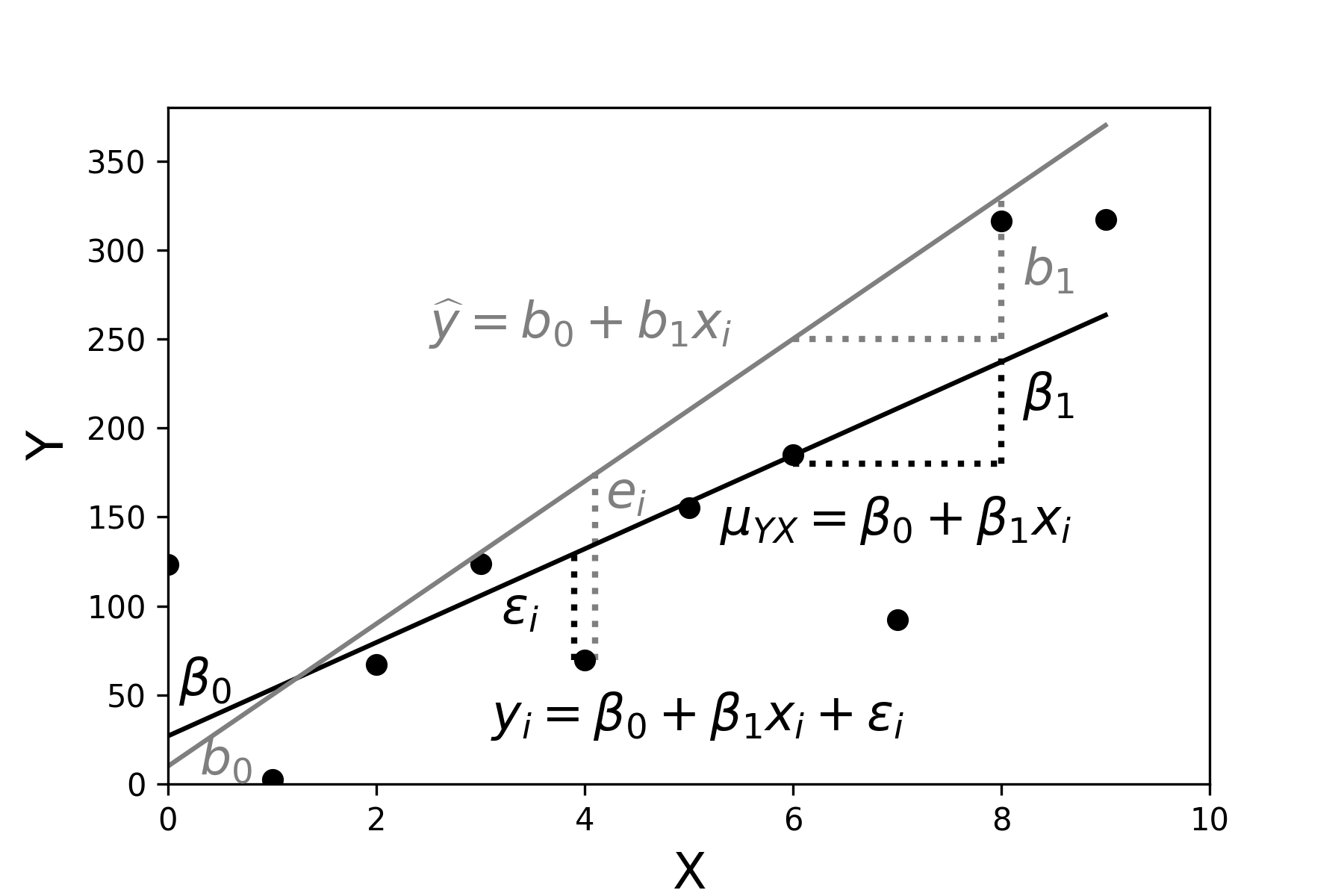
Dado que \(\epsilon\) se distribuye normal con media cero y varianza constante, el residuo \(e\) también deberá cumplir con los supuestos del modelo.
Los supuestos del modelo de regresión lineal son:
Normalidad
Los valores de \(Y\) se distribuyen normalmente para cada valor de \(X\)
La distribución del término de error es normal
Homocedasticidad, que significa varianza constante de \(Y\), con respecto a los valores de \(X\)
Independencia del valor de los errores con respecto a los valores de \(X\)
En términos simbólicos, podemos escribir los supuestos como:
\[\begin{aligned} Y\vert X &\sim& N(\overline{Y},\sigma_{\overline{Y}\vert X}) \nonumber \\ \epsilon &\sim& N(0,\sigma_{\epsilon}) \nonumber \\ \sigma_{Y_{i}}\!=\; & \sigma \vert X_{j} \quad \forall \quad j=1\cdots n \nonumber \\ E(\epsilon\vert X)\!=\; & E(\epsilon) \end{aligned}\]
Estimación por Máxima Verosimilitud
Bajos los supuestos antes mencionados, y con el objetivo de construir los Estimadores Máximo Verosímiles (EMV) \(b_{0}\) y \(b_{1}\) de los parámetros poblaciones \(\beta_{0}\) y \(\beta_{1}\), planteamos la función de verosimilitud (ver página ), que no es otra cosa que la función de probabilidad la cual se supone que sigue la variable aleatoria \(\epsilon\) (en este caso distribución normal con \(\mu=0\) y varianza \(\sigma^{2}\)), entonces:
\[\begin{aligned} l_{i}(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})\!=\; & \frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{1}{2\sigma^{2}}(\epsilon_{i})^{2}} \nonumber \\ \!=\; & \frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{1}{2\sigma^{2}}(Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2}} \end{aligned}\]
La función de verosimilitud conjunta para \(n\) observaciones aleatoriamente seleccionadas estará dada por:
\[\begin{aligned} L(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})\!=\; & \prod_{i=1}^{n}l_{i}(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i}) \nonumber \\ \!=\; & \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{1}{2\sigma^{2}}(Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2}} \nonumber \\ \!=\; & \bigg(\frac{1}{\sqrt{2\pi \sigma^{2}}}\bigg)^{n}e^{-\frac{1}{2\sigma^{2}}\sum_{i=1}^{n}(Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2}} \end{aligned}\]
Tomando logaritmo, tenemos:
\[\begin{aligned} \ln{L(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})}\!=\; & -\frac{n}{2}\ln{(2\pi)}-\frac{n}{2}\ln{\sigma^{2}}-\frac{1}{2\sigma^{2}}\sum_{i=1}^{n}(Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2} \end{aligned}\]
Calculando las derivadas parciales respecto a cada uno de los parámetros de la función conjunta de verosimilitud, llegamos a:
\[\begin{aligned} \frac{\partial \ln{L(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})}}{\partial \beta_{0}}\!=\; & \frac{1}{\sigma^{2}}\sum_{i=1}^{n}(Y_{i}-\beta_{0}-\beta_{1}X_{i}) \nonumber \\ \frac{\partial \ln{L(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})}}{\partial \beta_{1}}\!=\; & \frac{1}{\sigma^{2}}\sum_{i=1}^{n}X_{i}(Y_{i}-\beta_{0}-\beta_{1}X_{i}) \nonumber \\ \frac{\partial \ln{L(\beta_{0},\beta_{1},\sigma^{2},Y_{i},X_{i})}}{\partial \sigma^{2}}\!=\; & -\frac{n}{2}\frac{1}{\sigma^{2}}+\frac{1}{2(\sigma^{2})^{2}}\sum_{i=1}^{n}(Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2} \end{aligned}\]
Recordando que para obtener los estimadores que maximizan la función conjunta de verosimilitud tenemos que plantear las condiciones de primer orden, es decir las derivadas parciales respecto de \(\beta_{0}\), \(\beta_{1}\) y \(\sigma^{2}\) igualadas a cero16:
\[\begin{aligned} \label{cond_MV} \frac{1}{\widehat{\sigma}^{2}}\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})\!=\; & 0 \nonumber \\ \frac{1}{\widehat{\sigma}^{2}}\sum_{i=1}^{n}X_{i}(Y_{i}-b_{0}-b_{1}X_{i})\!=\; & 0 \nonumber \\ -\frac{n}{2}\frac{1}{\widehat{\sigma}^{2}}+\frac{1}{2(\widehat{\sigma}^{2})^{2}}\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})^{2}\!=\; & 0 \end{aligned}\]
De la primera condición obtenemos \(b_{0}\), haciendo:
\[\begin{aligned} \sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})\!=\; & 0 \nonumber \\ \sum_{i=1}^{n}Y_{i}-nb_{0}-b_{1} \sum_{i=1}^{n}X_{i} \!=\; & 0 \nonumber \end{aligned}\] \[\label{cond1} {b_{0}=\overline{Y}-b_{1}\overline{X}}\]
Operando sobre la segunda condición para encontrar \(b_{1}\), tenemos:
\[\begin{aligned} \sum_{i=1}^{n}X_{i}(Y_{i}-b_{0}-b_{1}X_{i}) \!=\; & 0 \nonumber \\ \sum_{i=1}^{n}X_{i}Y_{i}-b_{0} \sum_{i=1}^{n}X_{i} -b_{1}\sum_{i=1}^{n}X_{i}^{2} \!=\; & 0 \end{aligned}\]
Usando [cond1] y reemplazando,
\[\begin{aligned} \sum_{i=1}^{n}X_{i}Y_{i}-(\overline{Y}-b_{1}\overline{X})\sum_{i=1}^{n}X_{i} -b_{1}\sum_{i=1}^{n}X_{i}^{2} \!=\; & 0 \end{aligned}\]
Despejando \(b_{1}\),
\[\begin{aligned} \sum_{i=1}^{n}X_{i}Y_{i}-\overline{Y}\sum_{i=1}^{n}X_{i} +b_{1}\overline{X}\sum_{i=1}^{n}X_{i} -b_{1}\sum_{i=1}^{n}X_{i}^{2} \!=\; & 0 \nonumber \\ b_{1}(\sum_{i=1}^{n}X_{i}^{2}-\overline{X}\sum_{i=1}^{n}X_{i})\!=\; & \sum_{i=1}^{n}X_{i}Y_{i}-\overline{Y}\sum_{i=1}^{n}X_{i} \nonumber \\ b_{1}\!=\; & \frac{\sum_{i=1}^{n}X_{i}Y_{i}-\overline{Y}\sum_{i=1}^{n}X_{i}}{\sum_{i=1}^{n}X_{i}^{2}-\overline{X}\sum_{i=1}^{n}X_{i}} \end{aligned}\]
Aplicando propiedades de la sumatoria y luego dividiendo numerador y denominador por \(n-1\):
\[\begin{aligned} b_{1}\!=\; & \frac{\sum_{i=1}^{n}X_{i}Y_{i}-n\overline{Y}\overline{X}}{\sum_{i=1}^{n}X_{i}^{2}-n\overline{X}\overline{X}} \nonumber \\ \!=\; & \frac{\frac{\sum_{i=1}^{n}X_{i}Y_{i}-n\overline{Y}\overline{X}}{n-1}}{\frac{\sum_{i=1}^{n}X_{i}^{2}-n\overline{X}^{2}}{n-1}} \end{aligned}\]
Usando las expresiones ([covar_alternativa]) y ([varianza_muestral_ec]), tenemos:
\[\label{cond_b1} {b_{1}=\frac{Cov(X,Y)}{S^{2}_{x}}}\] que es el estimador máximo verosímil insesgado de \(\beta_{1}\).
Por último, es necesario calcular el estimador para \(\sigma^{2}\). Usando la tercera condición de primer orden, tenemos:
\[\begin{aligned} -\frac{n}{2}\frac{1}{\widehat{\sigma}^{2}}+\frac{1}{2(\widehat{\sigma}^{2})^{2}}\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})^{2}\!=\; & 0 \nonumber \\ -n+\frac{1}{\widehat{\sigma}^{2}}\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})^{2}\!=\; & 0 \nonumber \\ \widehat{\sigma}^{2}\!=\; & \frac{\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})^{2}}{n} \nonumber \end{aligned}\] \[\tcbhighmath[drop fuzzy shadow=white]{\widehat{\sigma}^{2}=\sum_{i=1}^{n}\frac{e_{i}^{2}}{n}}\] que es el EMV de \(\sigma^{2}\). Sin embargo, este estimador es sesgado y para obtener un estimador insesgado de la varianza se debe dividir por \(n-2\): \[\label{error_estandar} {S_{yx}^{2}=\sum_{i=1}^{n}\frac{e_{i}^{2}}{n-2}}\]
Estimación por Mínimos Cuadrados Ordinarios
Otra forma de calcular los estimadores \(b_{0}\) y \(b_{1}\) es mediante el método de Mínimos Cuadrados Ordinarios (MCO) que consiste en minimizar la suma de los cuadrados de los errores. Supongamos que tenemos un modelo lineal para explicar la relación entre la variable \(Y\) y \(X\), entonces, tal como se planteó anteriormente (ecuación [ecaucion_muestra]), escribimos:
\[\begin{aligned} Y_{i}\!=\; & b_{0}+b_{1} X_{i} + e_{i} \nonumber \\ \!=\; & \widehat{Y}_{i} +e_{i} \Rightarrow e_{i}=Y_{i}-\widehat{Y}_{i} \end{aligned}\]
Entonces, el método MCO plantea el siguiente problema de minimización:
\[\begin{aligned} \label{mco_def} && \min_{b_{0},b_{1}} \sum_{i=1}^{n}{(e_{i})^{2}} \nonumber \\ && \min_{b_{0},b_{1}} \sum_{i=1}^{n}{(Y_{i}-\widehat{Y}_{i})^{2}} \nonumber \\ && \min_{b_{0},b_{1}} f(b_{0},b_{1},Y_{i},X_{i})=\min_{b_{0},b_{1}} \sum_{i=1}^{n}{(Y_{i}-b_{0}-b_{1} X_{i})^{2}} \end{aligned}\]
Planteamos las condiciones de primer orden:
\[\begin{aligned} \frac{\partial f(b_{0},b_{1},Y_{i},X_{i})}{\partial b_{0}}\!=\; & -2\sum_{i=1}^{n}(Y_{i}-b_{0}-b_{1}X_{i})=0 \\ \frac{\partial f(b_{0},b_{1},Y_{i},X_{i})}{\partial b_{1}}\!=\; & -2\sum_{i=1}^{n}x_{i}(Y_{i}-b_{0}-b_{1}X_{i})=0 \end{aligned}\] que son las mismas condiciones que las obtenidas por la EMV (ver [cond_MV]). En consecuencia, los estimadores MCO para regresión lineal son idénticos a los EMV.
Con MCO se plantea la minimización de la suma del cuadrado de las distancias verticales que hay desde cada punto del diagrama hasta la recta \(\widehat{y}\), tal como se muestra en el gráfico:
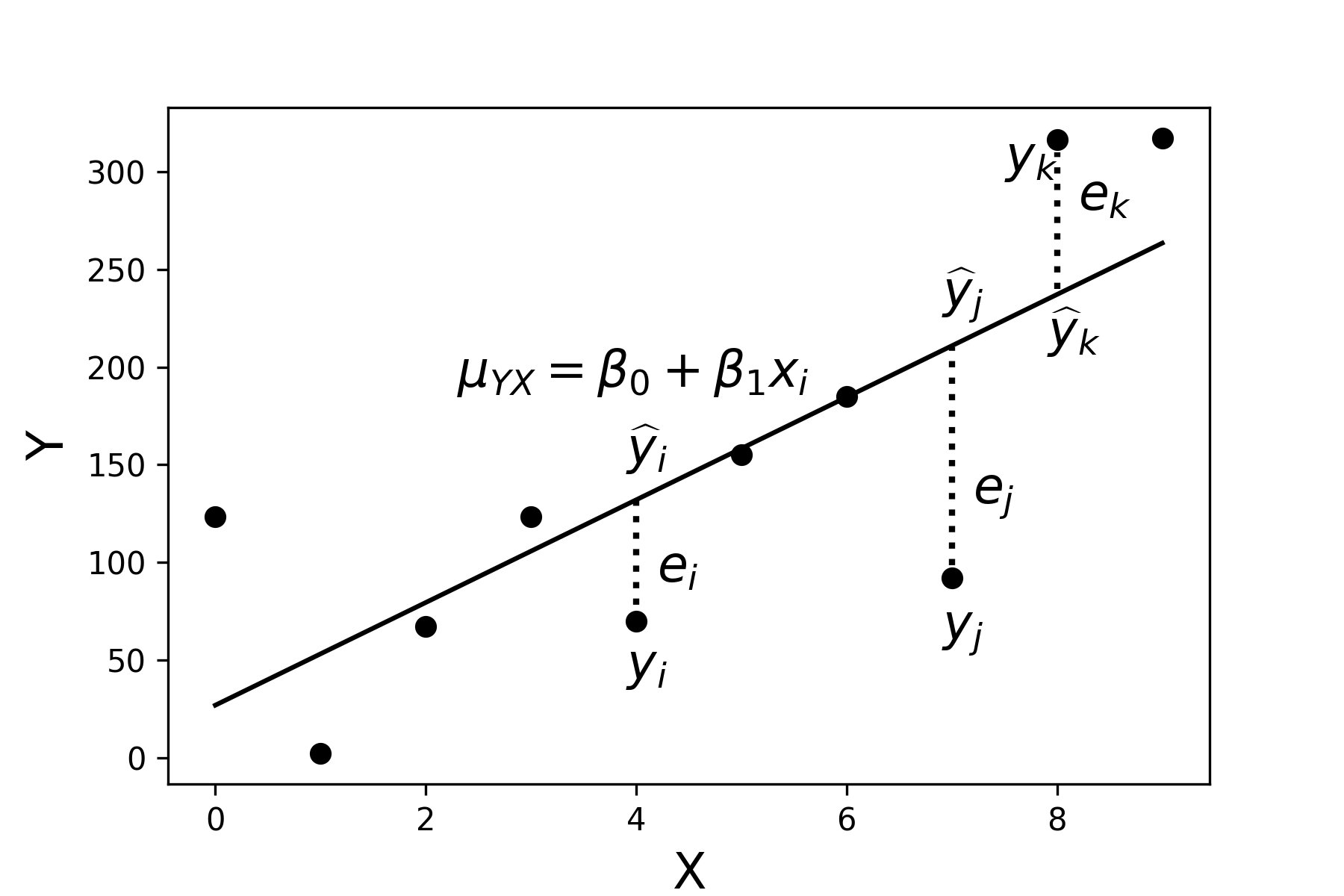
Los valores de \(b_{0}\) y \(b_{1}\) que satisfacen [mco_def], permiten, al mismo tiempo, que:
Se magnifiquen y/o penalicen, los errores más grandes
Se cancele el efecto de los valores positivos y negativos
Por otra parte, esta estimación también es válida aún cuando no se cumpla el supuesto de normalidad.
La distribución que sigue \(b_{0}\) es:
\[\begin{aligned} b_{0} & \sim & N\Big(\beta_{0},S_{yx}^{2}/n+\frac{ S_{yx}^{2}\overline{X}^{2}}{\sum (X_{i}-\overline{X})^{2}}\Big) \end{aligned}\]
El primer término de la varianza, \(S_{yx}^{2}/n\), corresponde al error de estimación de \(\overline{y}\), mientras que el segundo término, \(\frac{S_{yx}^{2}\overline{x}^{2}}{\sum (x_{i}-\overline{x})^{2}}\), tiene en cuenta que el error de estimación de la pendiente de la recta dada por la ordenada al origen es función de la distancia a la que se encuentre \(X\) respecto del origen de coordenadas, es decir que aumenta a medida que aumenta el valor de \(x\).
Para \(b_{1}\) su distribución es:
\[\begin{aligned} b_{1} &\sim & N\Big(\beta_{1},\frac{S_{yx}^{2}}{\sum (X_{i}-\overline{X})^{2}}\Big) \end{aligned}\] es decir que el valor \(b_{1}\) puede ser interpretado como un valor extraído al azar de una distribución normal con media \(\beta_{1}\) y varianza \(\frac{S_{yx}^{2}}{\sum (x_{i}-\overline{x})^{2}}\)
Inferencia sobre los coeficientes
La recta de regresión, tal como se mencionó antes, se deriva generalmente de una muestra y no de la población. Como resultado, no podemos esperar que la ecuación de la población \(Y=\beta_{0}+\beta_{1} X+\epsilon\) sea exactamente igual que la ecuación de la muestra \(y=b_{0}+b_{1}x+e\). Es por eso que se pueden usar los coeficientes estimados con los datos de la muestra para probar hipótesis respecto al valor de los parámetros \(\beta_{0}\) y \(\beta_{1}\). En general, planteamos: \[\begin{aligned} && H_{0}: \beta_{j}=\beta_{j}^{0} \nonumber \\ && H_{1}: \beta_{j} \neq \beta_{j}^{0} \quad \forall \quad j=0,1 \quad \textbf{Prueba bilateral} \nonumber \end{aligned}\] donde el supra-índice \(0\) indica el valor del parámetro bajo hipótesis nula.
El estadístico de la prueba es el siguiente: \[{\frac{b_{j}-\beta_{j}^{0}}{S_{b_{j}}} \sim t_{n-2}}\] siendo \[\begin{aligned} S_{b_{j}}=\frac{S_{yx}}{\sqrt{\sum(X_{i}-\overline{X})^{2}}} \end{aligned}\]
La importancia del test es porque permite dar respuesta a la pregunta sobre si el coeficiente, en términos estadísticos, es significativamente diferente de cero o no (bajo la hipótesis \(H_{0}: \beta_{j}=0\)). En el caso que sea significativo, es decir estadísticamente distinto de cero, entonces hay evidencia de la existencia de la relación funcional planteada entre las variables.
Coeficiente de Determinación \(R^{2}\)
El coeficiente \(R^{2}\) mide la intensidad de la relación entre las variables \(X\) e \(Y\). Se calcula relacionando dos tipos de variaciones de los valores de \(Y\):
\[\begin{aligned} R^{2}=\frac{SCR}{SCT}\!=\; & \frac{SCT-SCE}{SCT} \nonumber \\ \!=\; & 1-\frac{SCE}{SCT} \end{aligned}\] donde \(SCR\) es la suma de los cuadrados de la regresión, \(SCE\) suma de los cuadrados del error, y \(SCT\) suma de los cuadrados totales, es decir: \[\begin{aligned} SCR \!=\; & \sum_{i=1}^{n}(\widehat{Y}_{i}-\overline{Y})^{2} \nonumber \\ SCE \!=\; & \sum_{i=1}^{n}(Y_{i}-\widehat{Y}_{i})^{2} \nonumber \\ SCT \!=\; & \sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2} \end{aligned}\]
Si confeccionamos el gráfico de dispersión \(XY\) para representar las sumas de los cuadrados, tenemos:
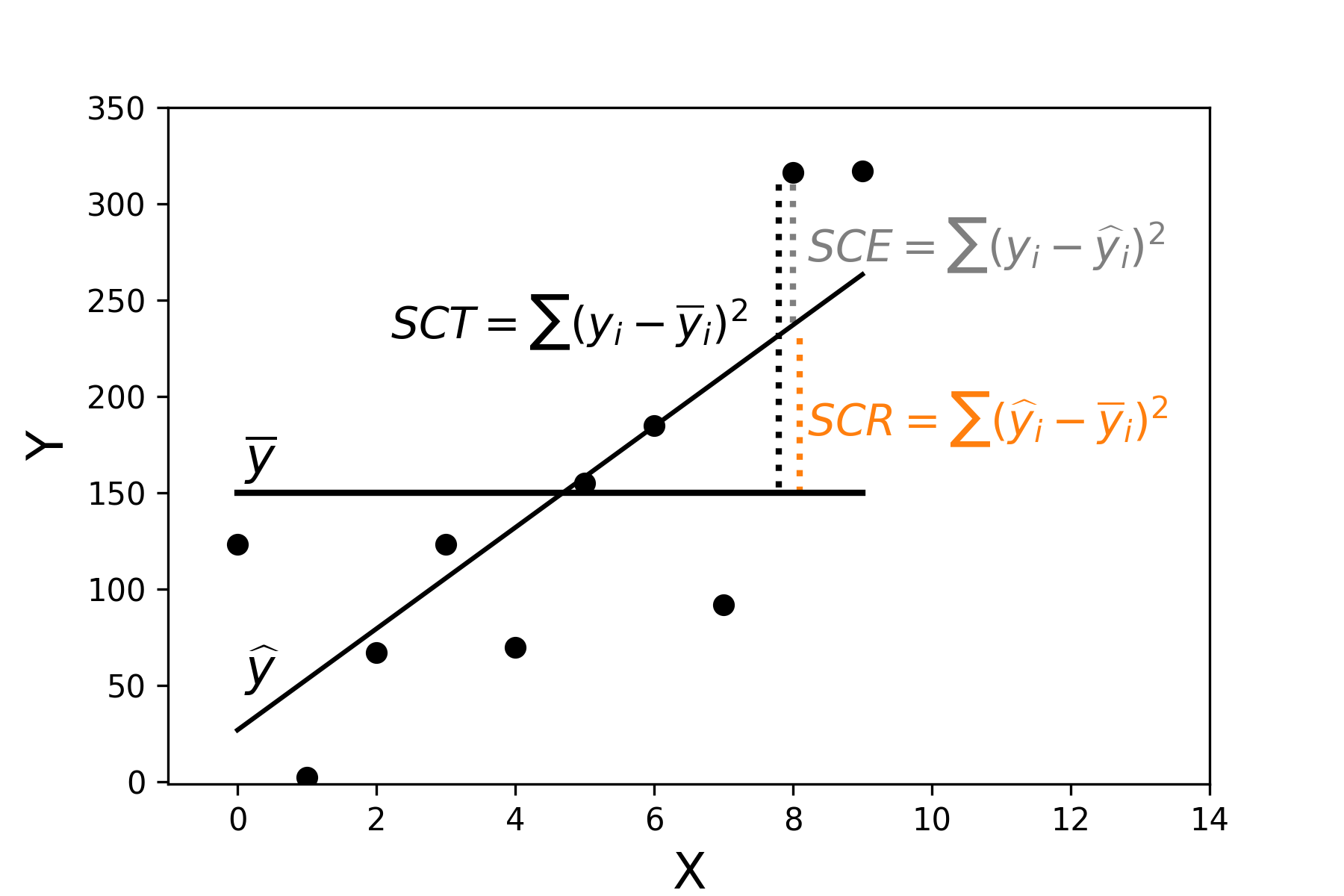
El \(R^{2}\) se interpreta como la proporción de variación de \(Y\) explicada por la regresión, con respecto a la variación total de \(Y\).
Relación entre los Coeficientes de Determinación y de Correlación Lineal
Consideremos el modelo lineal simple
\[\begin{aligned} Y_{i}\!=\; & \beta_{0}+\beta_{1} X_{i} + \epsilon_{i} \end{aligned}\] cuyos estimadores MCO de los coeficientes \(\beta_{0}\) y \(\beta_{1}\) son:
\[\begin{aligned} b_{0}\!=\; & \overline{Y}-b_{1}\overline{X} \nonumber \\ b_{1}\!=\; & \frac{Cov(X,Y)}{S^{2}_{x}} \end{aligned}\]
Sabemos que
\[\begin{aligned} R^{2}\!=\; & \frac{SCR}{SCT} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}(\widehat{Y}_{i}-\overline{Y})^{2}}{\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}}\nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}(b_{0}+b_{1}X_{i}-\overline{Y})^{2}}{\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}} \end{aligned}\]
Teniendo en cuenta que \(b_{0}=\overline{Y}-b_{1}\overline{X}\) (ver ecuación [cond1])
\[\begin{aligned} R^{2}\!=\; & \frac{\sum_{i=1}^{n}(\overline{Y}-b_{1}\overline{X}+b_{1}X_{i}-\overline{Y})^{2}}{\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}} \nonumber \\ \!=\; & \frac{\sum_{i=1}^{n}(b_{1}(X_{i}-\overline{X}))^{2}}{\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}} \nonumber \end{aligned}\] dividiendo numerador y denominador por \(n-1\) \[\begin{aligned} R^{2}\!=\; & b_{1}^{2}\Big(\frac{S_{x}}{S_{y}}\Big)^{2} \nonumber \end{aligned}\] y reemplazando \(b_{1}\) por el resultado obtenido en la ecuación ([cond_b1]), se obtiene: \[\begin{aligned} R^{2}\!=\; & \Big(\frac{Cov(X,Y)}{S^{2}_{x}}\Big)^{2}\Big(\frac{S_{x}}{S_{y}}\Big)^{2} \nonumber \\ \!=\; & \Big(\frac{Cov(X,Y)}{S_{x}S_{y}}\Big)^{2}=r^{2} \end{aligned}\]
Como conclusión, en el caso del modelo de regresión lineal simple, el coeficiente de determinación es igual al cuadrado del coeficiente de correlación.
Análisis de varianza de \(Y\)
La descomposición de la suma de los cuadrados es otra manera de analizar la calidad del modelo. Haciendo uso de la tabla de ANOVA (ver página ), descomponemos la suma total de los cuadrados de la diferencia de los valores de \(Y\) respecto a su media:
| Variación | Suma de Cuadrados | Grados de Libertad | Cuadrados Medios | F | p-valor |
| Regresión | \(SCR=\sum_{i=1}^{n}(\widehat{Y}_{i}-\overline{Y})^{2}\) | \(p\) | \(CMR=\frac{SCR}{p}\) | \(F=\frac{CMR}{CME}\) | \(p-valor\) |
| Error | \(SCE=\sum_{i=1}^{n}(Y_{i}-\widehat{Y}_{i})^{2}\) | \(n-p-1\) | \(CME=\frac{SCE}{n-p-1}\) | ||
| Total | \(SCT=\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}\) | \(n-1\) | \(CMT=\frac{SCT}{n-1}\) | ||
En consecuencia, podemos plantear la siguiente prueba de hipótesis para evaluar la dependencia lineal de los coeficientes de las variables independientes: \[\begin{aligned} && H_{0}: \beta_{1}=\beta_{2}=\cdots=\beta_{n}=0\nonumber \\ && H_{1}: \text{Alguno de los coeficientes es distinto de cero} \quad \textbf{Prueba unilateral derecha} \nonumber \end{aligned}\]
Como el cociente de varianzas tiene distribución \(F\), el estadístico de la prueba es: \[\begin{aligned} \frac{CMR} {CME} \sim F_{p,n-p-1} \end{aligned}\] donde \(p\) es el número de variables independientes del modelo y \(n\) el número de observaciones. Esta prueba también es conocida como prueba \(F\) o Global.
Se puede demostrar que en el caso de un modelo de regresión lineal simple, la prueba \(F\) es equivalente a la prueba sobre los coeficientes individuales (ver página ) desarrollada anteriormente.
Error de estimación del modelo
Utilizando el EMV insesgado para la varianza ([error_estandar]), cuyo denominador es \(n-2\) para corregir por sesgo, se puede escribir que el error de estimación del modelo viene dado por: \[\begin{aligned} S_{yx}\!=\; & \sqrt{\sum_{i=1}^{n}\frac{e_{i}^{2}}{n-2}} \nonumber \\ \!=\; & \sqrt{\frac{\sum_{i=1}^{n}(Y_{i}-\widehat{Y}_{i})^{2}}{n-2}} \nonumber \\ \!=\; & \sqrt{\frac{SCE}{n-2}} \end{aligned}\] donde SCE es la suma de los cuadrados del error. A \(S_{yx}\) se lo puede interpretar como la desviación estándar de la variación de las observaciones alrededor de la función del modelo de regresión.
Análisis Residual
Recordemos que los errores o residuos pueden calcularse como:
\[\begin{aligned} e_{i}=y_{i}-\widehat{Y_{i}}=Y_{i}-(b_{0}+b_{1}X_{i}) \end{aligned}\]
Estos residuos deben satisfacer con los supuestos planteados para el modelo, por lo que debemos verificar que se cumpla:
Los valores de \(Y\) se distribuyen normalmente para cada valor de \(X\)
La distribución del término de error es normal, lo cual se puede constatar a través de un QQ-Plot o bien, con una prueba de normalidad como Shapiro-Wills (ver página ) o bondad de ajuste (ver página ).
Homocedasticidad (varianza constante): se pueden analizar graficando los residuos en función de \(X\). Si este supuesto se cumple, los residuos deben estar acotados entre dos lineas paralelas al eje de las abscisas con dispersión relativamente homogénea entre dichas rectas a lo largo del eje \(X\).
Independencia de errores: no suele ser necesario verificar el cumplimiento de este supuesto cuando estamos en presencia de un modelo donde la variable regresora es el tiempo. Sin embargo, en caso de necesitar contrastar este supuesto, se lo puede hacer haciendo uso de la prueba de Durbin-Watson (ver página ).
Predicción
Cuando se quiere realizar predicciones de la variable \(Y\) a partir del modelo estimado, la precisión con la que se estima dicha variable es distinta si estamos hablando de la media condicional de \(Y\) o bien de valores puntuales; por dicho motivo el cálculo del intervalo de confianza para los pronósticos dependerá de si se trata de una u otra situación.
Predicción de valores medios
Cuando nos proponemos predecir una media condicional de \(Y\), la precisión vendrá dada por el siguiente intervalo de confianzas:
\[\begin{aligned} \label{pred_ind_media} \widehat{y}_{0}\pm t_{n-2} S_{yx} \sqrt{\frac{1}{n}+\frac{(x_{0}-\overline{X})^{2}}{(n-1)S^{2}_{x}}} \end{aligned}\]
Predicción de valores individuales
Cuando el objetivo es predecir la respuesta de \(Y\) ante un valor particular de \(X\), la estimación se realiza empleando:
\[\begin{aligned} \label{pred_ind} \widehat{y}_{0}\pm t_{n-2} S_{yx} \sqrt{1+\frac{1}{n}+\frac{(x_{0}-\overline{X})^{2}}{(n-1)S^{2}_{x}}} \end{aligned}\]
Como se puede apreciar, la precisión de la predicción de una media condicional es mayor que la predicción de un valor individual de \(Y\), ya que la amplitud del intervalo de confianza de ([pred_ind_media]) es menor que el intervalo de ([pred_ind]).
Problema Resuelto 6.2.
Mincer en 1974 propuso un modelo de regresión lineal como metodología para calcular la contribución del nivel educativo y de la experiencia (capacitación en el trabajo) en los ingresos de los trabajadores. La llamada “ecuación de Mincer”, en su versión más parsimoniosa, propone expresar los ingresos en función de los años de educación y de los años de experiencia en el mercado laboral. En esta instancia vamos a estimar dicha ecuación haciendo uso de una base de datos con 526 observaciones, pero en una versión aún más reducida del modelo, en el que sólo se tendrán en cuenta los años de educación de los trabajadores como variable independiente. El salario, medido en dólares por hora, será expresado en logaritmos. A continuación se presentan parcialmente las salidas de computación de la estimación realizada.
| Estadísticas de la regresión | |
|---|---|
| Coeficiente de determinación \(R^{2}\) | \(0.1858\) |
| Coeficiente de determinación \(R_{aj}^{2}\) | \(0.1843\) |
| Observaciones | 526 |
| Análisis de Variación | |||||
|---|---|---|---|---|---|
| Variación | Suma de Cuadrados | Grados de Libertad | Cuadrados Medios | F | p-valor |
| Regresión | \(27.56\) | ..... | ...... | ...... | ....... |
| Error | \(120.76\) | ..... | ...... | ||
| Total | ...... | ...... | ...... | ||
| Coeficientes | Error | t | p valor | Inferior | Superior | |
| \(\ln \textbf{Salario}\) | estándar | 95% | 95% | |||
| Constante | \(0.584\) | \(0.097\) | \(6.00\) | \(0.001\) | \(0.393\) | \(0.774\) |
| Educación | \(0.083\) | \(0.008\) | \(10.94\) | \(0.001\) | \(0.068\) | \(0.098\) |
Se pide:
Determinar la ecuación de la recta estimada
Completar la Tabla de ANOVA
Interpretar el valor del coeficiente estimado para la variable regresora
A un nivel de siginificancia de 5%, ¿existe evidencia de que la pendiente es distinta de cero? Indicar el p-valor de la prueba
¿Qué puede decir de la calidad del modelo?
Realizar una predicción por intervalo de confianza (\(1-\alpha=0.95\)) del salario medio horario para una persona con 17 años de educación formal, sabiendo que \(\overline{x}=12.56\) y \(s_{x}^{2}=7.67\).
Solución
La ecuación poblacional del modelo para esta versión resumida es:
\[\begin{aligned} \ln \textbf{Salario}_{i}\!=\; & \beta_{0}+\beta_{educ} \textbf{Educación}_{i}+\epsilon_{i} \end{aligned}\] donde \(\beta_{educ}\) es el coeficiente que multiplica a la variable “Educación”.17
La expresión de la ecuación muestral es:
\[\begin{aligned} \ln \textbf{Salario}_{i}\!=\; & b_{0}+b_{educ} \textbf{Educación}_{i}+e_{i} \end{aligned}\] donde \(b_{educ}\) es el estimador MCO para el parámetro poblacional \(\beta_{educ}\).
Por su parte, la ecuación estimada es:
\[\begin{aligned} \ln \textbf{Salario}_{i}\!=\; & 0.584+0.083 \cdot \textbf{Educación}_{i}+e_{i} \end{aligned}\]
Teniendo en cuenta la tabla ANOVA para regresión (ver página ), podemos completar la tabla de la siguiente manera:
| Análisis de Variación | |||||
|---|---|---|---|---|---|
| Variación | Suma de | Grados de | Cuadrados | F | p-valor |
| Cuadrados | Libertad | Medios | |||
| Regresión | \(27.56\) | \(p=1\) | \(CMR=27.56\) | \(F=119.58\) | \(\leq 0.0001\) |
| Error | \(120.77\) | \(n-p-1=524\) | \(CME=0.230\) | ||
| Total | \(SCT=148.33\) | \(n-1=525\) | \(CMT=0.283\) | ||
El valor del coeficiente estimado para la variable Educación es de \(0.083\), por lo que se puede interpretar que por cada año adicional de educación, el salario medio por hora aumenta en \(8.3\) %. Esta interpretación es debido a que la variable salario está expresada en logaritmos y el coeficiente \(b_{educ}\) es, entonces, la semi-elasticidad.
Para saber si el coeficiente que multiplica a la variable Educación es significativamente distinto de cero, se hace uso de la prueba de hipótesis sobre los coeficientes (ver página ), donde la hipótesis planteada es:
\[\begin{aligned} && H_{0}: \beta_{educ}=0 \nonumber \\ && H_{1}: \beta_{educ} \neq 0 \quad \textbf{Prueba bilateral} \nonumber \end{aligned}\]
El estadístico de la prueba es el siguiente: \[\begin{aligned} t_{obs}\!=\; & \frac{b_{educ}}{S_{b_{educ}}} \nonumber \\ \!=\; & \frac{0.083}{0.008}=10.94 \end{aligned}\]
Trabajando con un nivel del significancia del 5%, la zona de rechazo es:
\[\begin{aligned} \textbf{ZR}\!=\; & \lbrace t_{n-2} \in \mathbb{R} \vert t_{n-2}>t_{n-2}^{crit} \rbrace \nonumber \\ \!=\; & \lbrace t_{n-2} \in \mathbb{R} \vert t_{524}>1.96\rbrace \Rightarrow t_{obs}=10.94 \in \textbf{ZR} \end{aligned}\]
Por lo que se rechaza \(H_{0}\) ya que hay evidencia para decir que \(\beta_{educ}\) es significativamente distinto de cero en una relación funcional del tipo lineal, con un \(\alpha=0.05\).
Otra forma de analizar la prueba es comparando el p-valor con el nivel de significancia determinado para el análisis. Para ello retomemos los resultados de la estimación:
| Coeficientes | Error | t | p valor | Inferior | Superior | |
| \(\ln \textbf{Salario}\) | estándar | 95% | 95% | |||
| Constante | \(0.584\) | \(0.097\) | \(6.00\) | \(0.001\) | \(0.393\) | \(0.774\) |
| Educación | \(0.083\) | \(0.008\) | \(10.94\) | \(0.068\) | \(0.098\) |
Recordando que la regla de decisión dice que (ver página ):
\[\begin{aligned} p-valor > \alpha \qquad & \Rightarrow &\quad \textbf{No se rechaza la }H_{0} \nonumber \\ p-valor \leq \alpha \qquad & \Rightarrow &\quad \textbf{se rechaza la }H_{0} \nonumber \end{aligned}\]
En este caso
\[\begin{aligned} p-valor(\beta_{educ}) &\leq& \alpha \nonumber \\ 0.0001 &\leq& 0.05 \qquad \Rightarrow \quad \text{se rechaza la }H_{0} \nonumber \end{aligned}\]
Por último, podríamos haber realizado el análisis a través del intervalo de confianza del coeficiente que aparece en la referida salida:
| Coeficientes | Error | t | p valor | Inferior | Superior | |
| \(\ln \textbf{Salario}\) | estándar | 95% | 95% | |||
| Constante | \(0.584\) | \(0.097\) | \(6.00\) | \(0.001\) | \(0.393\) | \(0.774\) |
| Educación | \(0.083\) | \(0.008\) | \(10.94\) | \(0.001\) |
Allí podemos observar que el intervalo de confianza no incluye al cero, por lo que tenemos una confianza del 95% de que el verdadero valor del parámetro poblacional \(\beta_{educ}\) está entre \(0.068\) y \(0.098\).
Dado que estamos en un modelo de regresión lineal simple, la prueba Global o F, cuyo estadístico proviene de la tabla ANOVA, nos dará el mismo resultado que la prueba sobre el coeficiente \(\beta_{educ}\). Por lo tanto, rechazamos la hipótesis nula.
Para analizar la calidad global del modelo veremos también el coeficiente \(R^{2}\).
| Estadísticas de la regresión | |
|---|---|
| Coeficiente de determinación \(R^{2}\) | |
| Observaciones | 526 |
La interpretación del coeficiente de determinación \(R^{2}\) es que el modelo de regresión explica en un \(18.58\)% de la variación de la variable \(\ln \textbf{Salario}\).
Para hacer una predicción del logaritmo del salario que cobraría, en media, una persona con 17 años de educación formal, utilizaremos uso de la ecuación estimada anteriormente, es decir:
\[\begin{aligned} \ln \textbf{Salario}_{i}\!=\; & 0.584+0.083 \cdot \textbf{Educación}_{i}+e_{i} \nonumber \\ \ln \widehat{\textbf{Salario}_{i}}\!=\; & 0.584+0.083 \cdot 17 \nonumber \\ \!=\; & 1.995 \Rightarrow \widehat{\textbf{Salario}_{i}}= 7.35 \quad \text{USD/hora} \end{aligned}\]
Para calcular el intervalo de confianza a un nivel de 95% y, dado que nos estamos refiriendo a una predicción sobre la media, usamos la ecuación ([pred_ind_media]), \[\begin{aligned} \widehat{y}_{0}&\pm& t_{n-2} S_{yx} \sqrt{\frac{1}{n}+\frac{(x_{0}-\overline{X})^{2}}{(n-1)S^{2}_{x}}} \nonumber \\ 7,35&\pm& 1.96 \cdot \sqrt{\frac{120.77}{525-2}}\sqrt{\frac{1}{525}+\frac{(17-12.56)^{2}}{(525-1)7.67}} \nonumber \\ 7.35 &\pm & 0.08 \quad \text{USD/hora} \end{aligned}\]
En resumen, una persona con 17 años de educación formal, cobraría un salario por hora de \(7,35\) dólares y con una confianza del 95% el verdadero valor estará entre \(7.27\) y \(7.43\) dólares por hora.
Problema Resuelto 6.3. Se pretende estimar la relación entre el número de habitantes (\(X\)) de cada ciudad de Argentina (medido en millones) y el número de ventas de ejemplares (\(Y\)) de un cierto libro (medido en miles de unidades) en dicha ciudad. Una muestra tomada sobre cinco ciudades arroja los siguientes datos:
| \(\overline{x}\) | \(\overline{y}\) | \(\sum_{i=1}^{5}x^{2}_{i}\) | \(\sum_{i=1}^{5}y^{2}_{i}\) | \(\sum_{i=1}^{5}x_{i}y_{i}\) |
| 1 | 22 | 5,98 | 3 118 | 136 |
Se pide:
Construir un modelo de regresión lineal simple que modele las ventas del libro en función del número de habitantes de cada ciudad. Interprete los coeficientes del modelo.
Si la población de una localidad específica (por ejemplo es aproximadamente de 300 mil habitantes, efectúe una predicción de cuántos libros se venderían en dicha ciudad. ¿Es razonable, a un 95% de confianza, suponer que se venderán 12.000 libros? Suponga que \(\sum_{i}^{5}=e_{i}^{2}=8.21\), donde los \(e_{i}\) son los residuos de la regresión.
Contrastar mediante el p-valor si los habitantes producen un efecto lineal significativo en las ventas.
¿Cómo cambiarían los resultados del modelo de regresión si decidimos medir las ventas de libros en unidades y el número de habitantes en miles?
Solución
Sabiendo que el estimador de \(\beta_{1}\) es:
\[\begin{aligned} b_{1}\!=\; & \frac{\sum_{i=1}^{n}\frac{x_{i}y_{i}}{n}-\overline{y} \cdot \overline{x}}{\sum_{i=1}^{n}\frac{x_{i}^{2}}{n}-\overline{x}^{2}} \nonumber \\ \!=\; & \frac{{\frac{136}{5}-22 \cdot 1}}{\frac{5.98}{5}-1^{2}}=26.53 \end{aligned}\]
Por otra parte, \(b_{0}\) viene dado por:
\[\begin{aligned} b_{0}\!=\; & \overline{y}-b_{1}\overline{x} \nonumber \\ \!=\; & 22-26.53 \cdot 1 = -4.53 \end{aligned}\]
Por lo que la ecuación estimada es:
\[\begin{aligned} \widehat{y}=-4.53+26.53 x \end{aligned}\]
Haciendo uso de la recta estimada para predecir la cantidad vendida en la localidad de 300 mil habitantes, tenemos:
\[\begin{aligned} \widehat{y}\!=\; & -4.53+26.53 x \nonumber \\ \!=\; & -4.53+26.53 \frac{300\,000}{1\,000\,000}=3.43 \qquad \text{miles de libros} \end{aligned}\]
Esta es nuestra estimación puntual. Sin embargo, como sabemos, nos da más información la estimación por intervalos de confianza. Para ello se usa la ecuación [pred_ind] ya que queremos predecir un valor individual.
\[\begin{aligned} && \widehat{y}_{0}\pm t_{n-2} S_{yx} \sqrt{1+\frac{1}{n}+\frac{(x_{0}-\overline{x})^{2}}{(n-1)S^{2}_{X}}} \nonumber \\ && \widehat{Y}_{0}\pm t_{n-2} \sqrt{\frac{\sum_{i} e_{i}^{2}}{n-2}}\sqrt{1+\frac{1}{n}+\frac{(x_{0}-\overline{x})^{2}}{(n-1)\bigg(\sum_{i=1}^{n}\frac{x_{i}^{2}}{n}-\overline{x}^{2}\bigg)}} \nonumber \\ && 3.43 \pm t_{5-2} \sqrt{\frac{8.21}{5-2}}\sqrt{1+\frac{1}{5}+\frac{(0.3-1)^{2}}{(5-1) \big( \frac{5.98}{5} -1^{2}\big)}} \nonumber \\ &&3.43 \pm 3.18 \cdot 1.65 \sqrt{1.825} \nonumber \\ &&3.43 \pm 7.11 \quad \text{miles de libros} \end{aligned}\]
Por lo que no es razonable pensar que se venderán 12 mil libros, ya que el intervalo de confianza no contiene a dicho valor a un nivel del 95%.
Para ver si la población tiene un efecto lineal significativo sobre las ventas, vamos a hacer la prueba de hipótesis sobre los coeficientes (ver página ), donde:
\[\begin{aligned} && H_{0}: \beta_{1}=0 \nonumber \\ && H_{1}: \beta_{1} \neq 0\quad \textbf{Prueba bilateral} \nonumber \end{aligned}\]
El estadístico de la prueba es el siguiente: \[\begin{aligned} t_{n-2}=\frac{b_{1}-\beta^{0}}{S_{b_{1}}} \end{aligned}\] donde \[\begin{aligned} S_{b}=\frac{S_{yx}}{\sqrt{(n-1)S_{x}^{2}}} \end{aligned}\]
Calculando el valor del estadístico observado tenemos:
\[\begin{aligned} t_{obs}\!=\; & \frac{b_{1}-\beta_{1}^{0}}{\frac{S_{yx}}{\sqrt{(n-1)S_{x}^{2}}}} \nonumber \\ \!=\; & \frac{b_{1}-0}{\frac{\sqrt{\frac{\sum_{i} e_{i}^{2}}{n-2}}}{\sqrt{(n-1)S_{x}^{2}}}} \nonumber \\ \!=\; & \frac{26.53}{\frac{\sqrt{\frac{8.21}{5-2}}}{\sqrt{(5-1)\cdot 0.196}}} \nonumber \\ \!=\; & \frac{26.53}{1.86}=14.26 \nonumber \\ \end{aligned}\]
Recordando que el p-valor es el área comprendida entre el estadístico observado y \(+\infty\) multiplicado por dos, al realizar ese cálculo para el presente ejemplo, tendremos que da un valor de área inferior a \(0.001\). En consecuencia, usando un \(\alpha=0.05\), tenemos que p-valor\(\leq \alpha\) por lo que rechazamos \(H_{0}\), y podemos afirmar que existe un efecto lineal significativo de la cantidad de habitantes sobre las ventas.
Por último, recordando que el estimador para \(\beta_{1}\) es:
\[\begin{aligned} b_{1}=\frac{Cov(x,y)}{S^{2}_{x}} \end{aligned}\] y que la \(Cov(x,y)\) incorpora las unidades de medida de \(X\) y de \(Y\), mientras que \(S^{2}_{x}\) lleva la unidad de \(X\) al cuadrado, entonces, la unidad de \(b_{1}\) será:
\[\begin{aligned} [b_{1}]\!=\; & \frac{[X][Y]}{[X]^{2}} \nonumber \\ \!=\; & \frac{[Y]}{[X]} \end{aligned}\] donde los corchetes representan las unidades de medida de cada una de las variables. Es decir, \(b_{1}\) lleva la unidad de \(Y\) dividido la unidad de \(X\).
Inicialmente, la población (\(X\)) se expresaba en millones y las ventas de libros (\(Y\)) en miles, por lo tanto:
\[\begin{aligned} [b_{1}]\!=\; & \frac{[1\,000]}{[1\,000\,000]} \nonumber \\ \!=\; & \frac{[1]}{[1\,000]} \end{aligned}\]
Al cambiar la unidad de medida de la población a miles y la de ventas de libro a unidades, tenemos:
\[\begin{aligned} [b_{1}]\!=\; & \frac{[1]}{[1\,000]} \end{aligned}\] por lo que vemos que la unidad para el estimador \(b_{1}\) no se altera.
En el caso de \(b_{0}\), la unidad de medida es:
\[\begin{aligned} [b_{0}]=[\overline{Y}]-[b_{1}] \cdot [\overline{X}] \end{aligned}\] donde las unidades de medida de \(\overline{Y}\) y \(\overline{X}\) son las mismas unidades que la variable original, por lo tanto:
\[\begin{aligned} [b_{0}]\!=\; & [Y]-\frac{[Y]}{[X]} \cdot [X] \nonumber \\ \!=\; & [Y]-[Y]=[Y] \end{aligned}\]
Lo cual indica que \(b_{0}\) se mide en la misma unidad que la variable \(Y\). Si las ventas se expresan en la cantidad de libros en lugar de miles de libros vendidos, \(b_{0}\) se verá afectado y particularmente multiplicado por 1000, es decir que nuestro modelo estimado tomaría la forma siguiente:
\[\begin{aligned} \widehat{y}=-4\,530+26.53 x \end{aligned}\]
Por lo tanto, hay que tener en cuenta que, cuando se haga una predicción con este modelo donde \(X\) es la cantidad de libros, el resultado será expresado en unidades de libros a vender en lugar de miles de libros.
Regresión Lineal Múltiple
En el modelo de regresión lineal múltiple generalizamos el problema y ya no tenemos un solo regresor \(X\), sino que consideramos dos o más variables explicativas, es decir, la ecuación para la población vendrá dada por:
\[\begin{aligned} \label{reg_multiple} Y_{i}\!=\; & \underbrace{\beta_{0}+\beta_{1} X_{1i} +\beta_{2} X_{2i}+\cdots +\beta_{p} X_{pi}} +\epsilon_{i} \\ && \qquad \qquad \qquad \mu_{YX} \nonumber \end{aligned}\]
Por otra parte, la ecuación muestral será:
\[\begin{aligned} Y_{i}\!=\; & \underbrace{b_{0}+b_{1} X_{i} +b_{2} X_{2i}+\cdots +b_{p} X_{pi}}+ e_{i} \\ && \qquad \qquad \qquad \widehat{y} \nonumber \end{aligned}\] donde \(b_{0}\), \(b_{1},\cdots, b_{p}\) son los estimadores muestrales de los parámetros poblacionales \(\beta_{0}\), \(\beta_{1},\cdots, \beta_{p}\), respectivamente.
El modelo de regresión múltiple debe cumplir con los mismos supuestos que el modelo de regresión simple. Además, las pruebas de hipótesis sobre los coeficientes (ver página ), el análisis de varianza (ver página ), los coeficientes \(R^{2}\), \(R_{aj}^{2}\), y el error de estimación del modelo \(S_{yx}\) se analizan de manera análoga al modelo de regresión lineal simple.
Por otra parte, cada uno de los coeficientes se interpreta como los efectos marginales de \(Y\) respecto de \(X_{p}\), en otras palabras es el cambio que experimenta \(Y\) ante cambios unitarios de \(X_{p}\).
Coeficiente \(R^{2}\) ajustado
Este coeficiente se utiliza cuando se considera, como en [reg_multiple], más de una variable regresora (explicativa). Mide la intensidad de la relación entre la variable \(Y\) y el conjunto de variables \(X\), y corrige por cantidad de regresores o variables independientes que se incluyen en el modelo. Se define como:
\[\begin{aligned} R_{aj}^{2}\!=\; & 1- \frac{CME}{CMT} \end{aligned}\]
Desarrollando los cuadrados medios, el \(R_{aj}^{2}\) se puede expresar como:
\[\begin{aligned} R_{aj}^{2}\!=\; & 1-\bigg(1-\frac{SCR}{SCT}\bigg)\frac{n-1}{n-p-1} \nonumber \\ \!=\; & 1-(1-R^{2})\frac{n-1}{n-p-1} \end{aligned}\] donde \(p\) es la cantidad de regresores del modelo, y \(n\) el número de observaciones. El \(R_{aj}^{2}\) siempre toma valores inferiores al \(R^{2}\).
Prueba de Durbin-Watson
Cuando hay autocorrelación en el término de error \(\epsilon\), se viola uno de los supuestos en los que se basa el análisis de regresión. La prueba de Durbin-Watson se utiliza para medir la autocorrelación serial de primer orden, la cual se basa en los residuos de las estimaciones por MCO (ver página ). Si consideramos que \(\epsilon\) presenta autocorrelación de primer orden, entonces podemos escribir:
\[\begin{aligned} \epsilon_{t}=\gamma \epsilon_{t-1}+z_{t} \end{aligned}\] donde \(t\) se refiere al tiempo, \(\gamma\) es un coeficiente menor que 1 en valor absoluto, y \(z_{t}\) representa la parte del término de error no correlacionada. Si \(\gamma=0\) entonces el término de error \(\epsilon_{t}\) no tienen correlación de primer orden, mientras que si \(\gamma>0\) la correlación es positiva y si \(\gamma<0\) la correlación es negativa.
El estadístico de la prueba de Durbin-Watson es:
\[\begin{aligned} DW=\frac{\sum_{t=2}^{n} (e_{t}-e_{t-1})^{2}}{\sum_{t=1}^{n}e^{2}_{i}} \end{aligned}\]
Si desarrollamos el binomio del numerador y operamos llegamos a:
\[\begin{aligned} DW\!=\; & \frac{\sum_{t=2}^{n} (e_{t}-e_{t-1})^{2}}{\sum_{t=1}^{n}e^{2}_{i}} \nonumber \\ \!=\; & \frac{\sum_{t=2}^{n} e_{t}^{2}-2e_{t}e_{t-1}+ e_{t-1}^{2}}{\sum_{t=1}^{n}e^{2}_{i}} \nonumber \\ \!=\; & \frac{\sum_{t=2}^{n} e_{t}^{2}}{\sum_{t=1}^{n}e^{2}_{i}}-\frac{\sum_{t=1}^{n} 2e_{t}e_{t-1}}{\sum_{t=1}^{n}e^{2}_{i}}+\frac{\sum_{t=1}^{n} e_{t-1}^{2}}{\sum_{t=1}^{n}e^{2}_{i}} \end{aligned}\] donde el primero y el último término son aproximadamente uno, entonces:
\[\begin{aligned} DW&\approx&1-2\frac{\sum_{t=1}^{n} e_{t}e_{t-1}}{\sum_{t=1}^{n}e^{2}_{i}}+1 \nonumber \\ \!=\; & 2-2\frac{\sum_{t=1}^{n} e_{t}e_{t-1}}{\sum_{t=1}^{n}e^{2}_{i}} \end{aligned}\]
Por otra parte, el cociente del segundo término de la ecuación anterior es aproximadamente el coeficiente de correlación lineal (ver [coef_correl]) entre \(e_{t}\) y \(e_{t-1}\), por lo tanto el estadístico de DW puede ser aproximado a:
\[{DW\approx 2-2r}\]
Se puede observar fácilmente que el estadístico \(d\) toma valores entre 0 y 4. Si \(r\approx 0\) entonces el estadístico \(d\approx 2\), si \(r\to -1\) entonces \(d\to 4\) y por último, si \(r\to 1\) \(d\) tiende a 0. Durbin y Watson en 1950 obtuvieron la distribución de \(d\) y los límites inferiores (\(d_{L}\)) y superiores (\(d_{U}\)) para los cuales se determina la existencia de autocorrelación18. Esta distribución es condicional en \(X\), y depende de los valores de las variables independientes, como así también del tamaño de la muestra, del número de variables independientes y según que la regresión contenga o no un intercepto (\(\beta_{0}\)).
La prueba que generalmente se realiza es la siguiente:
\[\begin{aligned} H_{0}: &\quad& \text{No hay correlación entre los residuos} \nonumber \\ H_{1}: &\quad& \text{Hay correlación entre los residuos} \nonumber \end{aligned}\]
Teniendo en cuenta los valores que toma \(DW\) y los límites \(d_{L}\) y \(d_{U}\) podemos marcar las siguientes regiones:

Es decir que entre 0 y \(d_{L}\) hay evidencia de autocorrelación positiva, entre \(d_{U}\) y \(4-d_{u}\) no hay evidencia de autocorrelación, y entre \(4-d_{L}\) y 4 hay evidencia de autocorrelación negativa. Esta prueba no es concluyente para los intervalos de \((d_{L};d_{U})\) y \((4-d_{U};4-d_{L})\).
Endogeneidad
Supongamos que proponemos un modelo lineal simple
\[\begin{aligned} \label{mod_end} Y_{i}\!=\; & \beta_{0}+\beta_{1} X_{i} + \epsilon_{i} \end{aligned}\]
Cuando se viola el supuesto de \(E(X \epsilon)=0\), es decir, de independencia entre los valores de \(X\) y de \(\epsilon\), entonces podemos escribir
\[\begin{aligned} \epsilon_{i}=\gamma X_{i} + \epsilon_{i}^{*} \end{aligned}\] donde suponemos que \(\epsilon_{i}^{*}\) cumple todos los supuestos del modelo. Reemplazando
\[\begin{aligned} Y_{i}\!=\; & \beta_{0}+\beta_{1} X_{i} + \epsilon_{i} \nonumber \\ \!=\; & \beta_{0}+\beta_{1} X_{i} +\gamma X_{i} + \epsilon_{i}^{*} \nonumber \\ \!=\; & \beta_{0}+(\beta_{1}+\gamma )X_{i}+\epsilon_{i}^{*} \end{aligned}\]
Dado que nosotros planteamos el modelo [mod_end], estamos estimando como coeficiente de \(X\) a \(\beta_{1}\) cuando en realidad el valor es \(\beta_{1}+\gamma\), es decir el coeficiente estimado está sesgado a causa de alguna variable omitida que está correlacionada con \(X\)19.
Cuando estamos ante esta situación, conocida como problema de endogeneidad, el estimador que usualmente se utiliza para calcular los coeficientes es el que resulta de aplicar el “método con variables instrumentales”.
Colinealidad
Consideremos el siguiente modelo lineal múltiple
\[\begin{aligned} \label{colinealidad} Y_{i}\!=\; & \beta_{0}+\beta_{1} X_{1i} +\beta_{2} X_{2i} + \epsilon_{i} \end{aligned}\]
Supongamos que existe correlación entre \(X_{1}\) y \(X_{2}\), entonces podemos escribir que
\[\begin{aligned} X_{2i}=\xi X_{1i}+X_{2i}^{*} \end{aligned}\] donde ahora \(X_{2}^{*}\) es la parte de \(X_{2}\) que no está correlacionada con \(X_{1}\). Es decir, tenemos una variable \(X_{2}\) expresada como combinación lineal de \(X_{1}\) y \(X_{2}^{*}\). Reemplazando en [colinealidad], tenemos:
\[\begin{aligned} Y_{i}\!=\; & \beta_{0}+\beta_{1} X_{1i} +\beta_{2} (\xi x_{1i}+X_{2}^{*})+ \epsilon_{i} \nonumber \\ \!=\; & \beta_{0}+\beta_{1} X_{1i} +\beta_{2} \xi X_{1i}+\beta_{2} X_{2i}^{*}+ \epsilon_{i} \nonumber \\ \!=\; & \beta_{0}+(\beta_{1}+\beta_{2} \xi) X_{1i} +\beta_{2} X_{2i}^{*}+ \epsilon_{i} \nonumber \\ \end{aligned}\]
Aquí vemos que, si efectuamos las estimaciones del coeficiente de \(X_{1}\) en [colinealidad] tenemos un sesgo, dado que estamos estimando \(\beta_{1}\) cuando en realidad el coeficiente es \(\beta_{1}+\beta_{2} \xi\). La magnitud del sesgo vendrá dada por el valor de \(\xi\) que representará el grado de correlación entre las variables.
Para controlar este tipo de problemas, siempre hay que tratar de no incluir como regresores a variables que tengan una alta correlación entre sí, ya que explican aproximadamente lo mismo y el modelo pierde capacidad explicativa, porque no puede discernir a cuál de ellas atribuir los efectos. En ese caso, se deben suprimir las variables regresoras redundantes de modo que queden sólo aquellas con baja correlación, con lo cual la colinealidad se reducirá y, en consecuencia, los coeficientes no estarán sesgados debido a este efecto.
Problema Resuelto 6.4. Siguiendo con la ecuación de Mincer (ver problema de la página ), ahora proponemos un modelo ampliado en relación al anterior, donde usaremos como regresores, no sólo a los años de educación formal, sino también los años de experiencia, el sexo de la persona, el estado civil, y la cantidad de años de antigüedad en el trabajo actual. Los resultados de la estimación vienen dados parcialmente en las siguientes tablas.
| Estadísticas de la regresión | |
|---|---|
| Coeficiente de determinación \(R^{2}\) | \(0.4361\) |
| Coeficiente de determinación \(R_{aj}^{2}\) | \(0.4296\) |
| Observaciones | 526 |
| Análisis de Variación | |||||
|---|---|---|---|---|---|
| Variación | Suma de | Grados de | Cuadrados | F | p-valor |
| Cuadrados | Libertad | Medios | |||
| Regresión | \(64.69\) | ..... | ...... | ...... | ....... |
| Error | \(83.63\) | ..... | ...... | ||
| Total | ...... | ...... | ...... | ||
| Coeficientes | Error | t | p valor | Inferior | Superior | |
| \(\ln \textbf{Salario}\) | estándar | 95% | 95% | |||
| Constante | \(0.416\) | \(0.099\) | \(4.190\) | \(0.000\) | \(0.221\) | \(0.611\) |
| Educación | \(0.080\) | \(0.007\) | \(11.690\) | \(0.000\) | \(0.066\) | \(0.093\) |
| Experiencia | \(0.030\) | \(0.005\) | \(5.800\) | \(0.000\) | \(0.020\) | \(0.040\) |
| Experiencia\(^{2}\) | \(-0.001\) | \(0.000\) | \(-5.470\) | \(0.000\) | \(-0.001\) | \(0.000\) |
| Antigüedad | \(0.016\) | \(0.003\) | \(5.580\) | \(0.000\) | \(0.010\) | \(0.022\) |
| Mujer | \(-0.291\) | \(0.036\) | \(-8.020\) | \(0.000\) | \(-0.362\) | \(-0.220\) |
| Casado | \(0.056\) | \(0.041\) | \(1.380\) | \(0.168\) | \(-0.024\) | \(0.137\) |
Se pide:
Determinar la ecuación de la recta estimada
Completar la Tabla de ANOVA
Interpretar el valor del coeficiente estimado para todas variables regresoras
A un nivel de significancia de 5%, ¿existe evidencia de que las pendientes son distintas de cero? Indicar el p-valor de la prueba.
Realizar la prueba Global o F
¿Qué puede decir de la calidad del modelo?
¿Qué puede decir del modelo en comparación con el de regresión simple de una sola variable regresora (educación) antes desarrollado?
Solución
El modelo estimado de la ecuación de Mincer ampliada aquí planteado es:
\[\begin{aligned} \ln \textbf{Sal}_{i}\!=\; & \beta_{0}+\beta_{educ} \textbf{Educ}_{i}+\beta_{exp} \textbf{Exp}_{i}+\beta_{exp^{2}} \textbf{Exp}^{2}_{i}+\beta_{ant} \textbf{Ant}_{i}+\beta_{mujer} \textbf{Mujer}_{i}+\beta_{cas} \textbf{Cas}_{i}+\epsilon_{i} \nonumber \\ \ln \textbf{Sal}_{i}\!=\; & b_{0}+b_{educ} \textbf{Educ}_{i}+b_{exp} \textbf{Exp}_{i}+b_{exp^{2}} \textbf{Exp}^{2}_{i}+b_{ant} \textbf{Ant}_{i}+b_{mujer} \textbf{Mujer}_{i}+b_{cas} \textbf{Cas}_{i}+e_{i} \nonumber \\ \ln \textbf{Sal}_{i}\!=\; & 0.416+0.080 \cdot \textbf{Educ}_{i}+0.030 \cdot \textbf{Exp}_{i}-0.001 \cdot \textbf{Exp}^{2}_{i}+0.016 \cdot \textbf{Ant}_{i}-\nonumber \\ &-&0.291 \cdot \textbf{Mujer}_{i}+0.056 \cdot \textbf{Cas}_{i}+e_{i} \end{aligned}\]
Completando la Tabla de ANOVA
| Análisis de Variación | |||||
|---|---|---|---|---|---|
| Variación | Suma de | Grados de | Cuadrados | F | p-valor |
| Cuadrados | Libertad | Medios | |||
| Regresión | \(64.69\) | \(p=6\) | \(CMR=10.78\) | \(F=66.91\) | \(\leq 0.0001\) |
| Error | \(83.63\) | \(n-p-1=519\) | \(CMR=0.161\) | ||
| Total | \(SCT=148.32\) | \(n-1=525\) | \(CMT=0.282\) | ||
Las pendientes tienen distintas interpretaciones, según el tipo de variable:
Educación: por cada año adicional de educación, el salario aumenta un \(8.0\)%
Antigüedad: por cada año adicional de antigüedad en el trabajo, el salario aumenta un \(1.6\)%
Experiencia: esta variable debe ser analizada en conjunto con Experiencia al cuadrado. Es común incorporar el cuadrado de una variable cuando se cree que puede haber crecimiento o decrecimiento de escala. Dado que el coeficiente de la variable Experiencia al cuadrado es negativo, significa que tendremos un máximo en algún punto de la experiencia, y dicho punto puede ser calculado como \(-b_{exp}/(2b_{exp^{2}})\)20, es decir \(-b_{exp}/(2b_{exp^{2}})=-0,030/(-2\cdot 0.001)=15\) por lo tanto, el salario aumentará hasta los 15 años de experiencia.
Mujer: esta variable es del tipo dicotómica, es decir toma el valor 1 cuando el sexo del encuestado es femenino y cero en caso contrario. Por lo que su interpretación es en relación al estado base (cuando vale cero). En este caso sería que cuando el encuestado es de sexo femenino, el salario disminuye un \(29.1\)%
Casado: es otra variable dicotómica al estilo de Mujer. Se define igual a uno cuando el encuestado es casado y cero en caso contrario. Sin embargo, esta variable no tiene sentido que sea analizada debido a que el posible valor cero de su coeficiente está incluido en el intervalo de confianza \((-0,024;0,137)\) a un 95%, por lo que no hay evidencia de que pueda ser distinto de cero.
Analizando los p-valores para la prueba sobre los coeficientes, en todos los casos se rechaza \(H_{0}: \beta_{i}=0\), a excepción del coeficiente de la variable Casado, para el cual no existe evidencia de que tenga una relación funcional lineal, en coeficientes, con el logaritmo del salario.
En cuanto a la prueba Global o F, donde la hipótesis es:
\[\begin{aligned} && H_{0}: \beta_{educ}=\beta_{exp}=\beta_{exp^{2}}=\beta_{ant}=\beta_{muj}=\beta_{cas}=0\nonumber \\ && H_{1}: \text{Alguno de los coeficientes es distinto de cero} \nonumber \end{aligned}\]
El estadístico de esta prueba es el que se obtuvo en la tabla ANOVA, donde \(F_{obs}=66.91\). Si consideramos el p-valor de la prueba, y con un \(\alpha=0.05\), rechazamos la \(H_{0}\), por lo que alguno de los coeficientes es significativamente distinto de cero.
El coeficiente \(R^{2}\) indica que el modelo explica el \(43.61\)% de la variación del logaritmo del salario. El \(R_{aj}^{2}\) está levemente por debajo del \(R^{2}\) lo que indicaría que las variables incorporadas en el modelo tienen poder explicativo.
Comparando el modelo con el estimado en el problema anterior (ver problema 6.2), podemos ver que el \(R^{2}\) es muy superior cuando incorporamos otras variables explicativas (\(0,4296\) contra \(0,1843\)). Es decir, este segundo modelo propuesto explica un mayor porcentaje de variación de \(Y\) respecto al modelo simple.
Problema Resuelto 6.5. Se desea analizar cómo influye la estatura de una persona en su peso. Para ello se toma una muestra aleatoria de 19 personas entre 18 y 65 años y se obtiene la siguiente información:
| Id Persona | Estatura | Peso | Id Persona | Estatura | Peso |
| (cm) | (kg) | (cm) | (kg) | ||
| 1 | 176 | 60 | 11 | 165 | 90 |
| 2 | 168 | 75 | 12 | 160 | 95 |
| 3 | 170 | 65 | 13 | 170 | 130 |
| 4 | 151 | 67 | 14 | 165 | 70 |
| 5 | 171 | 68 | 15 | 165 | 75 |
| 6 | 162 | 63 | 16 | 165 | 63 |
| 7 | 156 | 56 | 17 | 165 | 80 |
| 8 | 160 | 70 | 18 | 152 | 70 |
| 9 | 175 | 86 | 19 | 172 | 67 |
| 10 | 155 | 55 |
Realizar un ajuste por mínimos cuadrados ordinarios
Escribir la ecuación de la recta estimada
Analizar si el coeficiente estimado de la pendiente es significativamente distinto de cero usando un \(\alpha=0.05\)
Analizar la calidad del modelo a través del coeficiente de determinación
Solución
Lo primero que debemos hacer es plantear la ecuación que deseamos estimar. Dado que queremos ver cómo influye la estatura en el peso, la ecuación a estimar es:
\[\begin{aligned} \text{Peso}_{i}=\beta_{0}+\beta_{1} \text{Estatura}_{i}+\epsilon_{i} \end{aligned}\]
Para estimar los coeficientes del modelo se hará uso del siguiente código, teniendo en cuenta que el arreglo de datos “x” tiene en cada columna las variables exógenas del modelo y que, para que el modelo estime con constante, es decir con \(\beta_{0}\), debemos introducir una columna de unos que, en este caso, es la primer columna del arreglo “x”. El arreglo de “y” viene en una sola fila de datos. Hay que tener en cuenta que la cantidad de filas del arreglo de “x” debe coincidir con la cantidad de columnas del arreglo de “y”.
import statsmodels.api as sm
import numpy as np
# Datos de todas las variables exogenas del modelo. Si se desea
# estimar con constante, se debe incluir un uno como primer vector
x = [[1,176],
[1,168],
[1,170],
[1,151],
[1,171],
[1,162],
[1,156],
[1,160],
[1,175],
[1,155],
[1,165],
[1,160],
[1,170],
[1,165],
[1,165],
[1,165],
[1,165],
[1,152],
[1,172]]
# Datos de la variable de respuesta y
y = [60,75,65,67,68,63,56,70,86,55,90,95,130,70,75,63,80,70,67]
x, y = np.array(x), np.array(y)
if x.shape[0]!=y.shape[0]:
print("Error en la dimension de los arreglos x e y")
elif x.shape[0]==y.shape[0]:
results = sm.OLS(y,x).fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.062
Model: OLS Adj. R-squared: 0.007
Method: Least Squares F-statistic: 1.127
Date: Mon, 10 Aug 2020 Prob (F-statistic): 0.303
Time: 09:11:15 Log-Likelihood: -80.024
No. Observations: 19 AIC: 164.0
Df Residuals: 17 BIC: 165.9
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -23.1222 91.542 -0.253 0.804 -216.259 170.014
x1 0.5906 0.556 1.061 0.303 -0.583 1.764
==============================================================================
Omnibus: 17.414 Durbin-Watson: 1.395
Prob(Omnibus): 0.000 Jarque-Bera (JB): 17.873
Skew: 1.738 Prob(JB): 0.000131
Kurtosis: 6.240 Cond. No. 3.80e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.8e+03. This might indicate that there are
strong multicollinearity or other numerical problems.La ecuación estimada es:
\[\begin{aligned} \text{Peso}_{i}=-23.1222+0.5906 \quad \text{Estatura}_{i}+e_{i} \end{aligned}\]
Para analizar la significancia de la pendiente, es decir del coeficiente \(\beta_{1}\), tenemos que analizar el p-valor de la prueba sobre los coeficientes. En este caso el p-valor es \(0.303\) por lo que No se rechaza la hipótesis nula, por lo tanto, el coeficiente de la pendiente no es significativamente distinto de cero. Esto significa que, o bien no existe relación funcional lineal entre la estatura y el peso, o el tamaño de muestra es pequeño y no tenemos suficiente información para estimar el efecto.
El coeficiente de determinación es \(0.062\), es decir, el modelo sólo explica el 6,2% de la variabilidad del peso.
Para analizar el supuesto de independencia del error utilizamos el estadístico DW. Los valores de \(d_{L}\) y \(d_{U}\), que están tabulados, para un tamaño de muestra \(n=19\), una variable independiente y un \(\alpha=0,01\), son \(d_{L}=0,928\) y \(d_{U}=1,133\). Por lo tanto en el rango \((1,133; 2,867)\) no se detecta autocorrelación. El estadístico estimado de Durbin-Watson es de \(1,395\), incluido en el intervalo anterior, por lo que se concluye que no hay presencia de autocorrelación en los residuos de este modelo.
Problema Resuelto 6.6. Una empresa quiere lanzar al mercado un nuevo celular. Para ello desea conocer el impacto que tienen en el precio distintas características del mismo, tales como la densidad de PPI de la pantalla, el tipo de display, el tamaño de la pantalla, la cantidad de megapixeles de la cámara, la memoria interna, la cantidad de carga máxima de la batería, la memoria RAM, y la marca. Para tal fin, se selecciona una muestra aleatoria de distintos modelos de celulares y se recolecta la información relacionada al precio y todas las otras variables (ver smartphones.xlsx). Si bien los gerentes están interesados en conocer la relación en general de todas las características con el precio, tienen particular interés entre el precio y la densidad de PPI de la pantalla.
Solución
Dado que la empresa quiere analizar el impacto de la densidad de PPI de la pantalla en el precio, vamos a plantear un modelo lineal simple en logaritmos para así poder interpretar el coeficiente como elasticidad. Entonces tenemos:
\[\begin{aligned} \ln{\text{Precio}}_{i}=\beta_{0}+\beta_{1} \ln{\text{PPI}}_{i}+\epsilon_{i} \end{aligned}\]
Por otra parte, los celulares que no disponen de información del año de lanzamiento o marca21, no serán tenidos en cuenta en la estimación de nuestro modelo, y la muestra se restringirá a las principales marcas de celulares, dado que hay un gran número de fabricantes. Posteriormente incluiremos controles por marcas.
Además, vamos a suponer que todos los requisitos que se deben cumplir para aplicar la estimación por mínimos cuadrados se cumplen. Por lo tanto, podemos escribir el siguiente código, donde ahora la lectura de los datos proviene de un archivo Excel22, para lo cual debemos indicar en el código, cuál es el directorio donde se aloja dicho archivo.
import statsmodels.api as sm
import numpy as np
import pandas as pd
from patsy import dmatrices
# Path del directorio donde se encuentran los datos
path = r"/My_path/"
# Lectura de archivo Excel con el nombre de la hoja
data = pd.read_excel(path+'/smartphones.xlsx',sheet_name='smartphones',header=0).dropna(subset=['price', 'ppi', 'camera', 'mem', 'size'])
def dummy(var,d,c):
data[c]=0
data.loc[data[var]==d,c]=1
return
dummy('brand','Apple','Apple')
dummy('brand','Samsung','Samsung')
dummy('brand','Nokia','Nokia')
dummy('brand','Motorola','Motorola')
dummy('brand','Huawei','Huawei')
dummy('release',2011,'y2011')
dummy('release',2012,'y2012')
dummy('release',2013,'y2013')
dummy('release',2014,'y2014')
dummy('release',2015,'y2015')
dummy('release',2016,'y2016')
dummy('release',2017,'y2017')
data['lprice']=np.log(data['price'])
data['lweight']=np.log(data['weight'])
data['lppi']=np.log(data['ppi'])
data['lcamera']=np.log(data['camera'])
data['lmem']=np.log(data['mem'])
data['lsize']=np.log(data['size'])
ecuacion='lprice ~ lppi'
y, X = dmatrices(ecuacion, data=data, return_type='dataframe')
results = sm.OLS(y,X).fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: lprice R-squared: 0.365
Model: OLS Adj. R-squared: 0.364
Method: Least Squares F-statistic: 1474.
Date: Fri, 14 Aug 2020 Prob (F-statistic): 2.86e-255
Time: 08:03:11 Log-Likelihood: -1512.2
No. Observations: 2571 AIC: 3028.
Df Residuals: 2569 BIC: 3040.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.7637 0.156 -4.905 0.000 -1.069 -0.458
lppi 1.0660 0.028 38.392 0.000 1.012 1.120
==============================================================================
Omnibus: 29.480 Durbin-Watson: 1.227
Prob(Omnibus): 0.000 Jarque-Bera (JB): 33.535
Skew: 0.206 Prob(JB): 5.22e-08
Kurtosis: 3.378 Cond. No. 105.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Por lo tanto, el modelo estimado es:
\[\begin{aligned} \ln{\text{Precio}}_{i}=-0.7637+1.0660 \ln{\text{PPI}}_{i}+e_{i} \end{aligned}\] donde el coeficiente que acompaña a la variable exógena “PPI” se interpreta directamente como una elasticidad e indica que a medida que aumenta un 1% la densidad de PPI de la pantalla, el precio aumenta un 1,07%, es decir estamos en el tramo elástico de la demanda. Analizando la prueba sobre el coeficiente, observamos que se rechaza la hipótesis nula y es significativamente distinto de cero con un estadístico \(t=38.392\). Además, el coeficiente de determinación es \(0.365\), indicando que el modelo explica un \(36.5\)% de la variabilidad del precio de los celulares de la muestra.
Sin embargo, dado que podemos estar omitiendo variables que podrían estar correlacionadas con la densidad de píxeles, y como disponemos de otras variables de control, entonces plantearemos un modelo lineal múltiple. Es importante recordar que si hay variables omitidas que están correlacionadas con alguna de las variables incluidas en el modelo, podemos tener problemas de endogeneidad, y si las variables capturan la misma característica del celular, tendremos problemas de colinealidad. En consecuencia, hay que analizar correctamente las variables de control a incorporar en un modelo.
Incorporaremos la marca y el año de fabricación, que son variables cualitativas que se deben introducir como variables dicotómicas (dummy en inglés) para poder capturar el efecto de dicha categoría sobre el precio, en relación a una categoría que se debe omitir para evitar multi-colinealidad. Es decir, si consideramos la marca “Apple”, entonces la variable categórica, que denominaremos “Apple”, tomará el valor uno cuando el celular sea de ese fabricante y cero en caso contrario. Este tipo de tratamiento se realiza con las variables del tipo cualitativo. Sin embargo, cuando la variable tiene “muchas” categorías, se generan demasiadas dummies, ya que se incorpora una por cada categoría. En esos casos, la sugerencia en agrupar en categorías más amplias. Tal es el caso de la marca, en donde tenemos demasiadas categorías. Es por ello que nos concentraremos solo en algunas marcas (Apple, Samsung, Nokia, Motorola, Amazon y Huawei) y resto de celulares serán incluidos en una categoría residual que será la dummy omitida. Entonces, el modelo es:
\[\begin{aligned} \ln{\text{Precio}}_{i}\!=\; & \beta_{0}+\beta_{1} \ln{\text{PPI}}_{i}+\beta_{2} \ln{\text{Camara}}_{i} +\beta_{3} \ln{\text{Memoria}}_{i}+ \beta_{4} \ln{\text{Size}}_{i}+ \nonumber \\ &+& \gamma D_{marca}+\delta D_{\text{año fab}}+\epsilon_{i} \end{aligned}\] donde \(D_{marca}\) es el conjunto de variables dicotómicas de las principales marcas, \(D_{\text{año fab}}\) el conjunto de variables dicotómicas que indican el año de fabricación (toman el valor uno en ese año y cero en caso contrario), “Camara” la cantidad de mega píxeles que tiene la cámara de fotos del celular, “Memoria” la cantidad de memoria RAM, “Size” el tamaño de la pantalla medido en pulgadas, y \(\epsilon\) el término de error.
Entonces, generando las dummies de marca y año de fabricación y siguiendo con el código anterior, pero cambiando la ecuación del modelo, podemos estimar los coeficientes.
ecuacion='lprice ~ lppi + lcamera + lmem + lsize + Apple + Samsung + Nokia + Motorola + Huawei + y2011 + y2012 + y2013 + y2014 + y2015 + y2016 + y2017'
y, X = dmatrices(ecuacion, data=data, return_type='dataframe')
results = sm.OLS(y,X).fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: lprice R-squared: 0.585
Model: OLS Adj. R-squared: 0.583
Method: Least Squares F-statistic: 225.2
Date: Fri, 14 Aug 2020 Prob (F-statistic): 0.00
Time: 08:01:57 Log-Likelihood: -963.84
No. Observations: 2571 AIC: 1962.
Df Residuals: 2554 BIC: 2061.
Df Model: 16
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.9586 0.196 4.882 0.000 0.574 1.344
lppi 0.4872 0.038 12.978 0.000 0.414 0.561
lcamera 0.2975 0.020 14.557 0.000 0.257 0.338
lmem 0.1970 0.013 15.576 0.000 0.172 0.222
lsize 0.4888 0.041 11.809 0.000 0.408 0.570
Apple 0.5174 0.078 6.626 0.000 0.364 0.671
Samsung 0.1767 0.021 8.312 0.000 0.135 0.218
Nokia -0.0456 0.045 -1.009 0.313 -0.134 0.043
Motorola 0.0700 0.035 1.977 0.048 0.001 0.139
Huawei 0.0540 0.030 1.827 0.068 -0.004 0.112
y2011 -0.1630 0.038 -4.238 0.000 -0.238 -0.088
y2012 -0.0812 0.034 -2.417 0.016 -0.147 -0.015
y2013 -0.2238 0.032 -6.906 0.000 -0.287 -0.160
y2014 -0.3481 0.032 -11.035 0.000 -0.410 -0.286
y2015 -0.5292 0.034 -15.782 0.000 -0.595 -0.463
y2016 -0.5834 0.036 -16.145 0.000 -0.654 -0.513
y2017 -0.5180 0.043 -11.993 0.000 -0.603 -0.433
==============================================================================
Omnibus: 203.480 Durbin-Watson: 1.216
Prob(Omnibus): 0.000 Jarque-Bera (JB): 351.033
Skew: 0.574 Prob(JB): 5.95e-77
Kurtosis: 4.400 Cond. No. 193.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.La ecuación del nuevo modelo estimado:
\[\begin{aligned} \ln{\text{Precio}}_{i}\!=\; & 0.9586+0.4872 \cdot \ln{\text{PPI}}_{i}+0.2975 \cdot \ln{\text{Camara}}_{i} +0.1970 \cdot \ln{\text{Memoria}}_{i}+ 0.4888 \cdot \ln{\text{Size}}_{i}+ \nonumber \\ &+& 0.5174 \cdot \text{Apple}+ 0.1767 \cdot \text{Samsung} -0.0456 \cdot \text{Nokia} + 0.0700 \cdot \text{Motorola} +\nonumber \\ &+& 0.0540 \cdot \text{Huawei} -0.1630 \cdot \text{Fab 2011} -0.0812 \cdot \text{Fab 2012} -0.2238 \cdot \text{Fab 2013} - \nonumber \\ &-& 0.3481 \cdot \text{Fab 2014} -0.5292 \cdot \text{Fab 2015} -0.5834 \cdot \text{Fab 2016} -0.5180 \cdot \text{Fab 2017} + e_{i} \nonumber \end{aligned}\]
Analizando los coeficientes estimados y las pruebas de hipótesis realizadas, vemos que se rechazan las \(H_{0}\) en todos los casos al 1%, exceptuando la variable “Nokia” que es no significativa, y las variables “Motorola” y “Huawei” son significativas al 5% y 10% respectivamente. Además, de acuerdo a los coeficientes de marcas, podemos observar que un celular del fabricante ‘Àpple’’ tiene un precio 51,74% superior en relación a las otras marcas omitidas en la ecuación estimada, mientras que “Nokia” no tiene un precio significativamente superior.
Por otra parte, el coeficiente estimado de la densidad de píxeles, tiene un coeficiente estimado de 0,4872, es decir que a medida que aumenta un 1% la densidad de píxeles, el precio aumenta un 0,4872%. Este valor es considerablemente inferior al obtenido con el modelo anterior. Ello podría deberse a que el modelo anterior era un planteo muy sencillo y las variables omitidas, que estaban incorporadas en el término de error, podrían haber estado correlacionadas con la densidad de píxeles, es decir un problema de endogeneidad. Por eso es importante hacer un correcto análisis de posibles variables omitidas en el modelo ya que podrían sesgar los coeficientes de los regresores de la ecuación.
En el caso de la prueba global F (tabla ANOVA para regresión), el valor del estadístico de la prueba es 225,2 con un p-valor inferior al 1%, por lo que se rechaza la \(H_{0}\) de que todos los coeficientes a la vez son cero, en consecuencia uno o más es distinto de cero.
Si analizamos el coeficiente de determinación \(R^{2}\) y el ajustado \(R^{2}_{aj}\) observamos que, con este modelo, explicamos poco más del 58% de la variabilidad del precio de los celulares, lo que representa una importante mejora respecto del modelo lineal simple anterior. Sin embargo, cabe destacar que aquí no se abordó en ningún momento posibles problemas de endogeneidad mencionados anteriormente.
Anexo
En el presente anexo se encuentran otros scripts para el cálculo de probabilidades que pueden ser de utilidad para el lector.
Distribución Normal Estándar
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from scipy.stats import norm
import scipy.stats as st
# Probabilidad acumulada a izquierda
alfa=0.05
normal = stats.norm(0, 1)
x = np.linspace(normal.ppf(0.0001),
normal.ppf(0.9999), 100)
fp = normal.pdf(x)
plt.plot(x, fp,color='black')
plt.ylabel('Densidad')
plt.xlabel('Z')
plt.rcParams["font.size"] = "10"
z=normal.ppf(alfa)
x2 = np.linspace(normal.ppf(0.0001),
normal.ppf(alfa), 100)
fp2 = normal.pdf(x2)
plt.fill_between(x2, 0, fp2, color='tab:gray')
plt.show()
print("El valor de z para una probabilidad acumulada a izquierda de ",alfa," es:",z)
# Valor de z que acumula probabilidad a izquierda
z=-1.64
normal = stats.norm(0, 1)
alfa = normal.cdf(z)
print("La probabilidad acumulada a izquierda hasta un valor z ",z," es:",alfa)Distribución \(\chi^{2}\)
from scipy import stats
from scipy.stats import chi2
chi_obs=6 #valor del chi2
n=10 #grados de libertad
chi2 = stats.chi2(n)
alfa=chi2.sf(chi_obs)
print("La probabilidad acumulada a derecha hasta un valor chi2 ",chi_obs," es:",alfa)
alfa=0.05 #valor del chi2
n=10 #grados de libertad
chi2 = stats.chi2(n)
chi_obs=chi2.ppf(1-alfa)
print("El valor de chi2 para una probabilidad acumulada a derecha de ",1-alfa," es:",chi_obs)Distribución F
from scipy import stats
from scipy.stats import f
f_obs=6 #valor del chi2
n=10 #grados de libertad numerador
m=10 #grados de libertad denominador
f = stats.f(n,m)
alfa=f.sf(f_obs)
print("La probabilidad acumulada a derecha de un valor F ",f_obs," es:",alfa)
alfa=0.05 # probabilidad acumulada a derecha
n=10 #grados de libertad numerador
m=10 #grados de libertad denominador
f = stats.f(n,m)
f_obs = f.ppf(1-alfa)
print("El valor de F para una probabilidad acumulada a derecha de ",1-alfa," es:",f_obs)Distribución t
from scipy import stats
from scipy.stats import norm
df = 300 # grados de libertad
alfa=0.05
t = stats.t(df)
t_obs = t.ppf(alfa)
print("El valor de t para una probabilidad acumulada a izquierda de ",alfa," es:",t_obs)
# Valor de t para probabilidad acumulada a izquierda
t_obs=-1.96
df = 300 # grados de libertad
t = stats.t(df)
alfa = t.sf(t_obs)
print("La probabilidad acumulada a izquierda de un valor t ",t_obs," es:",1-alfa)Función de Potencia
Este script calcula la función de potencia para una prueba cuyo estadístico sigue una distribución normal estándar y, para los tres tipos de hipótesis (unilateral derecha, izquierda y bilateral).
import numpy as np
from scipy import stats
from scipy.stats import expon
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm
mu, sigma = 0, 1 # media y desvio estandar
normal = stats.norm(mu, sigma)
#Parametros
u0=80
n=64
sigma=15
alfa=0.01
u1=pd.DataFrame(np.ones(shape=(41,1)))
u1=u1.index+60
#Prueba izquierda
z_iz=norm.ppf(alfa)
x_crit_iz=u0+z_iz*sigma/n**0.5
z_pot_iz=pd.DataFrame(np.ones(shape=(41,1)))
z_pot_iz=(x_crit_iz-u1)/(sigma/n**0.5)
potencia_iz=pd.DataFrame(np.ones(shape=(41,1)))
potencia_iz=norm.cdf(z_pot_iz)
#Prueba derecha
z_de=norm.ppf(1-alfa)
x_crit_de=u0+z_de*sigma/n**0.5
z_pot_de=pd.DataFrame(np.ones(shape=(41,1)))
z_pot_de=(x_crit_de-u1)/(sigma/n**0.5)
potencia_de=pd.DataFrame(np.ones(shape=(41,1)))
potencia_de=1-norm.cdf(z_pot_de)
#Prueba bilaretal
z_bi1=norm.ppf(alfa/2)
z_bi2=norm.ppf(1-alfa/2)
x_crit_bi1=u0+z_bi1*sigma/n**0.5
x_crit_bi2=u0+z_bi2*sigma/n**0.5
z_pot_bi1=pd.DataFrame(np.ones(shape=(41,1)))
z_pot_bi1=(x_crit_bi1-u1)/(sigma/n**0.5)
z_pot_bi2=pd.DataFrame(np.ones(shape=(41,1)))
z_pot_bi2=(x_crit_bi2-u1)/(sigma/n**0.5)
potencia_bi=pd.DataFrame(np.ones(shape=(41,1)))
potencia_bi=norm.cdf(z_pot_bi1)+(1-norm.cdf(z_pot_bi2))
plt.title(r'Funcion de Potencia para $\mu_{0}=80$')
plt.ylabel(r'$\phi(\mu_{1})$')
plt.xlabel(r'$\mu_{1}$')
plt.xticks([])
plt.plot(u1, potencia_bi, '-ok', color='black')
plt.savefig(r'/content/func_pot_bi.png',dpi=300)
plt.title(r'Funcion de Potencia para $\mu_{0}=20$')
plt.ylabel(r'$\phi(\mu_{1})$')
plt.xlabel(r'$\mu_{1}$')
plt.xticks([])
plt.plot(u1, potencia_de, '-ok', color='black')
plt.savefig(r'/content/func_pot_de.png',dpi=300)
plt.title(r'Funcion de Potencia para $\mu_{0}=20$')
plt.ylabel(r'$\phi(\mu_{1})$')
plt.xlabel(r'$\mu_{1}$')
plt.xticks([])
plt.plot(u1, potencia_iz, '-ok', color='black')
plt.savefig(r'/content/func_pot_iz.png',dpi=300)Notas de pie de página
Llamaremos grados de libertad al número de observaciones que puede variar libremente después que alguna restricción ha sido calculada, por ejemplo, cuando ya se obtuvo la media muestral.↩︎
Para programar en Python es recomendable instalar Anaconda, que es de distribución libre y abierta. Anaconda incluye distintas aplicaciones en las cuales se pueden ejecutar los códigos, tales como Jupyter Notebook o Spyder. Por otra parte, también se puede utilizar Google Colab que es una versión on-line donde se pueden crear Notebooks y en la que se pueden correr procesos de varias horas de duración, haciendo uso de máquinas virtuales.↩︎
La cota de Rao-Cramer expresa una cota inferior para la varianza de un estimador insesgado, es decir la varianza mínima a la cuál podría llegar un estimador.↩︎
La función de verosimilitud es el producto de las funciones de probabilidad individuales, por tratarse de la probabilidad de presentación conjunta, es decir simultánea, de \(n\) observaciones que son independientes entre sí.↩︎
Nótese que la función de verosimilitud para estimar \(P\) es la función de cuantía Binomial, ya que expresa la probabilidad conjunta de sumatorio de \(x_{i}\) éxitos en \(n\) pruebas.↩︎
En este caso, si no se cumpliese el supuesto de poblaciones normales, el tamaño de muestra mayor a 30 hace que también sea válido el estadístico aplicado en la estimación↩︎
Hay innumerables situaciones similares en donde las muestras observadas presentan dependencia.↩︎
En algunas ocasiones aparecen efectos temporales que afectan de distinta manera a las mediciones en \(t_{1}\) y \(t_{2}\). Estos efectos, que exceden el análisis de este libro, también deben ser controlados para no incurrir en conclusiones erróneas.↩︎
Se denota con un supraíndice “\(o\)” a las frecuencias observadas y con un supraíndice “\(e\)” a las frecuencias esperadas.↩︎
Este límite es un valor práctico generalmente aceptado.↩︎
La corrección de Yates se utiliza cuando al menos una frecuencia esperada es menor a 5.↩︎
En lugar del punto medio también pueden ser usados los mínimos o máximos de cada intervalo como aproximación del valor de \(X\) de ese intervalo↩︎
También conocida como curva OC por sus siglas en inglés.↩︎
En el caso de no conocer el parámetro poblacional \(\pi\) se usa el valor de \(0.5\) que maximiza el tamaño de muestra.↩︎
La autocorrelación de una variable es la correlación de dicha variable a lo largo del tiempo, es decir:
\(\rho_{t,t-k}=\frac{COV(X_{t},X_{t-k})}{\sigma_{X_{t}}^{2}}, \quad \forall k\)↩︎Al plantear las derivadas parciales igualadas a cero, reemplazamos los parámetros poblacionales \(\beta_{0}\), \(\beta_{1}\) y \(\sigma^{2}\) por sus respectivos estimadores muestrales \(b_{0}\), \(b_{1}\) y \(\widehat{\sigma}^{2}\) cuyos valores queremos calcular.↩︎
En el planteo del modelo, \(\beta_{educ}\) era representado por \(\beta_{1}\).↩︎
Los límites \(d_{L}\) y \(d_{U}\) son valores que se encuentran tabulados para distintos tamaños de muestra y cantidad de variables independientes que se incorporen al modelo.↩︎
Se conoce como “sesgo por variable omitida”↩︎
La deducción de dicha expresión proviene de igualar a cero la primera derivada de la función cuadrática \(\beta_{exp} \textbf{Exp} + \beta_{exp^{2}} \textbf{Exp}^{2}\), que es condición necesaria para la existencia de un máximo↩︎
Los celulares que no tienen esa información tienen como respuesta “NA” en la base de datos.↩︎
Para descargar el archivo Excel ir Github: dgiuliodori/estadistica_ii
Allí se encuentran todos los scripts desarrollados en este libro.↩︎